समाधानकर्ताओं गणना

स्पर्शरेखा रेखा कैलकुलेटर

सराय: किसी दिए गए फ़ंक्शन के लिए स्पर्शरेखा रेखा की गणना करने के लिए इस कैलकुलेटर का उपयोग करें, किसी दिए गए बिंदु पर, सभी चरणों को दिखाते हुए।कृपया फ़ंक्शन में टाइप करें और नीचे दिए गए फॉर्म बॉक्स में संबंधित बिंदु।

इस स्पर्शरेखा रेखा कैलकुलेटर के बारे में

यह कैलकुलेटर आपको एक फ़ंक्शन की स्पर्शरेखा रेखा को प्राप्त करने के लिए आवश्यक गणना का संचालन करने की अनुमति देगा, एक दिए गए बिंदु पर, सभी चरणों को दिखाते हुए।

आपको बस एक वैध फ़ंक्शन f (x) प्रदान करना है, और एक बिंदु जहां आप स्पर्शरेखा रेखा चाहते हैं।फ़ंक्शन किसी भी मान्य, अलग -अलग फ़ंक्शन की तरह हो सकता है जैसे f (x) = sin (x), या f (x) = x^2 - x + 1, आदि। बिंदु किसी भी मान्य संख्यात्मक अभिव्यक्ति हो सकता है, जैसे 1/2 के लिएउदाहरण।

फिर, जब आवश्यक जानकारी प्रदान की गई है, और यह मान्य है, तो आपको आपको दिखाए गए स्पर्शरेखा रेखा समीकरण के सभी चरणों को प्राप्त करने के लिए "गणना" पर क्लिक करना होगा।

स्पर्शरेखा रेखा अनुप्रयोग चारों ओर विज्ञान में लाजिमी है।यह भी कहा जाता है अफ़र , यह भौतिकी और इंजीनियरिंग में वास्तव में कुछ गहरा अर्थ है, जहां बदलने के लिए मुख्य योगदान का विचार (पहला आदेश भाग) वह है जो एक प्रक्रिया के बारे में बहुत सारी जानकारी का अनावरण करता है।

स्पर्शरेखा रेखा क्या है

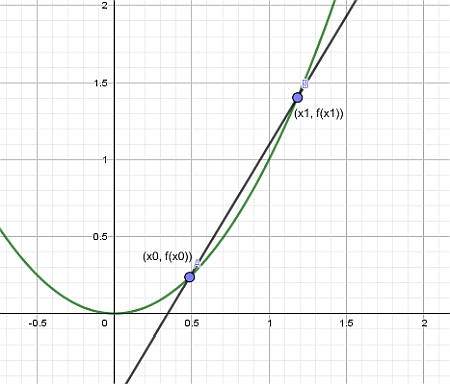
In simple terms, a tangent line is a line that intersects a curve, but it intersects it at one point only (at least locally). This tangent line is constructed by fixing a point \(x_0\) and then taking a different point \(x_1\).

फिर, उस लाइन का निर्माण करके जो अंक \((x_0, f(x_0))\)और \((x_1, f(x_1))\)से गुजरता है, हमें वह मिलता है जिसे कहा जाता है अराधुरी , जैसा कि नीचे दिए गए ग्राफ में दिखाया गया है:

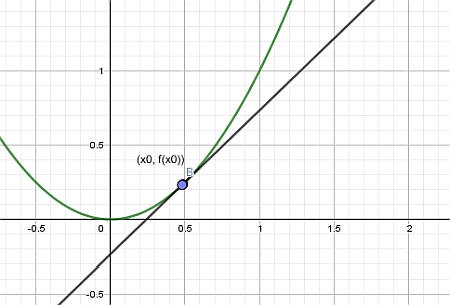
अंत में, हम \(x_0\)के लिए \(x_1\)दृष्टिकोण करते हैं, और हमें जो मिलता है वह स्पर्शरेखा रेखा है:

स्पर्शरेखा रेखा को ज्यामितीय रूप से खोजने के लिए कदम

स्टेप 1: उस फ़ंक्शन f (x) को पहचानें, जिसके साथ आप काम करना चाहते हैं, और बिंदु X0।आपको दोनों की जरूरत है
Their दो दो: बिंदु (x0, f (x0)) फ़ंक्शन f (x) के वक्र पर होगा।इसे प्लॉट करना
Theirण 3: एक X1 के लिए एक बिंदु (x1, f (x1)) चुनें, जो X0 से अलग है (x के बाएं या दाएं तक हो सकता है)।इसे प्लॉट करना
च ४: ४: अंक (x0, f (x0)) और (X1, f (x1)) के माध्यम से गुजरने वाली एक लाइन ड्रा करें
च ५: ५: एक बिंदु x2 चुनें जो X0 और X1 के बीच आधा है, और अंक (x0, f (x0)) और (x2, f (x2)) के माध्यम से गुजरने वाली एक रेखा खींचें
च viry: 6: इस प्रक्रिया को कुछ बार दोहराएं

यह ग्राफिकल विधि आपको इस बात का एक मोटा विचार प्राप्त करने में सहायता करेगी कि स्पर्शरेखा रेखा कैसे दिखती है, लेकिन एक अनुमान है (जब तक कि फ़ंक्शन f (x) रैखिक नहीं है)।

स्पर्शरेखा रेखा सूत्र

सेकंट लाइनों का उपयोग करने वाली सन्निकटन विधि आपको इस बात का अंदाजा दे सकती है कि आप क्या देख रहे हैं, लेकिन सौभाग्य से, एक बिंदु \(x_0\)पर एक फ़ंक्शन के लिए स्पर्शरेखा रेखा की गणना करने के लिए एक सटीक सूत्र है।स्पर्शरेखा रेखा सूत्र है:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

सरल, हुह?सरल शब्दों में, यह सूत्र यह बता रहा है कि स्पर्शरेखा रेखा एक है रत्न जो बिंदु से से गुज गुज \((x_0, f(x_0))\)और जिसमें\(m = f'(x_0)\)की ढलान है

फिर, आसान शब्दों में, किसी दिए गए बिंदु पर स्पर्शरेखा रेखा का ढलान उस बिंदु पर फ़ंक्शन का व्युत्पन्न है।

स्पर्शरेखा रेखा सूत्र को लागू करने के लिए कदम

Letsunt 1: फ़ंक्शन f (x) और बिंदु X0 को पहचानें
Their दो दो: X0 पर फ़ंक्शन के मान की गणना करें, जो F (x0) है
Theirण 3: बिंदु X0 पर f (x) के व्युत्पन्न की गणना करें, इसलिए आपको f '(x0) की आवश्यकता है
च ४: ४: सीधे स्पर्शरेखा रेखा \(y = f(x_0) + f'(x_0) (x - x_0)\)का सूत्र लागू करें

एक बार आपके पास है तंग अणु , आप इसे उस प्रारूप में बदल सकते हैं जो हाथ में स्थिति के लिए सबसे उपयोगी है।

स्पर्शरेखा रेखा का ढलान

प्रमुख takeaways में से एक यह है कि \(x_0\)पर स्पर्शरेखा रेखा का ढलान बिल्कुल \(f'(x_0)\)है, जो कि बिंदु \(x_0\)पर व्युत्पन्न है।यह ज्यामितीय शब्दों में व्युत्पन्न की एक स्पष्ट और अत्यंत उपयोगी व्याख्या प्रदान करता है।

यह कनेक्शन केवल फ़ंक्शन के व्युत्पन्न को देखकर किसी दिए गए बिंदु पर किसी दिए गए वक्र के लिए स्पर्शरेखा रेखा के समीकरण को खोजने की अनुमति देता है।

When do you have a horizontal tangent line?

एक क्षितिज स्पर्शरेखा रेखा तब होगी जब \(x_0\) चुना गया बिंदु # जब उस बिंदु पर संबंधित व्युत्पन्न शून्य के बराबर हो।उस स्थिति में स्पर्शरेखा रेखा (जो कि लाइन है जो स्थानीय रूप से एक बिंदु पर वक्र को छूती है) y- अक्ष के समानांतर होगी।

इसलिए, क्षैतिज स्पर्शरेखा लाइनों की पहचान करने के लिए आपको सभी को जानना होगा कि उन बिंदुओं को ढूंढना है जहां फ़ंक्शन का व्युत्पन्न शून्य है।

आपके पास एक ऊर्ध्वाधर स्पर्शरेखा रेखा कब है?

एक ऊर्ध्वाधर स्पर्शरेखा रेखा तब होगी जब व्युत्पन्न एक बिंदु पर "अनंत" हो।यह कहने का एक सरल तरीका है कि यह वह जगह है जहां व्युत्पन्न को किसी दिए गए बिंदु पर परिभाषित नहीं किया गया है, लेकिन यह अनंत में परिवर्तित हो जाता है क्योंकि हम बिंदु पर पहुंचते हैं।

उदाहरण के लिए, कोई यह कह सकता है कि \(f(x) = \frac{1}{x}\) में x = 0. पर एक ऊर्ध्वाधर स्पर्शरेखा रेखा है, हालांकि, यह तर्क दिया जा सकता है कि कोई स्पर्शरेखा रेखा नहीं है क्योंकि व्युत्पन्न को x = 0 पर अच्छी तरह से परिभाषित नहीं किया गया है।

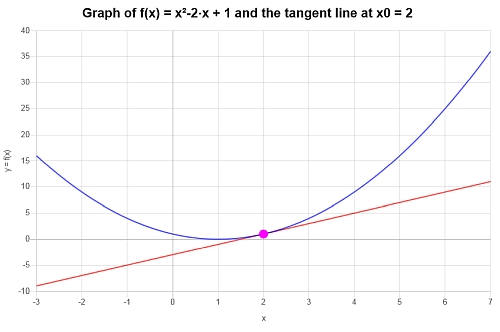
उदाहरण: स्पर्शरेखा रेखा

\(f(x) = x^2 - 2x + 1\)के लिए स्पर्शरेखा रेखा के समीकरण का पता लगाएं, बिंदु \(x_0 = 2\)पर।

समाधान: निम्न फ़ंक्शन वह है जिसके साथ हमें काम करने की आवश्यकता है: \(\displaystyle f(x)=x^2-2x+1\)।सबसे पहले, हमें इसके व्युत्पन्न की गणना करने की आवश्यकता है।

फ़ंक्शन पहले से ही सरल हो गया, इसलिए हम सीधे इसके व्युत्पन्न की गणना करने के लिए आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(x^2-2x+1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-2x+1 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\)

Since the derivative of a constant is 0, we find that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)\)

Directly we get: \(\frac{d}{dx}\left( 2x \right) = 2\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2\)

तमाम : फ़ंक्शन \(\displaystyle f(x)=x^2-2x+1\) के लिए स्पर्शरेखा रेखा का समीकरण \(x_0 = 2\) है:

\[y = y_0 + f'(x_0)(x - x_0) \]

इस मामले में, \(\displaystyle y_0 = f(x_0)\), इसलिए फ़ंक्शन में \(x_0 = 2\)के मान को प्लग करना होता है:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

इसके अलावा, गणना की गई व्युत्पन्न लीड पर बिंदु \(x_0 = 2\) के मान को प्लग करना:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

तो, अब हम इन मूल्यों को प्राप्त करने के लिए स्पर्शरेखा रेखा सूत्र में प्लग करते हैं:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

तिहाई : इसलिए, यह पाया जाता है कि फ़ंक्शन \(\displaystyle f(x)=x^2-2x+1\) के लिए स्पर्शरेखा रेखा \(x_0 = 2\) है:

\[y = 2x-3 \]

दिए गए फ़ंक्शन और इसकी स्पर्शरेखा लाइन \(x_0 = 2\)के लिए निम्न प्लॉट प्राप्त किया जाता है:

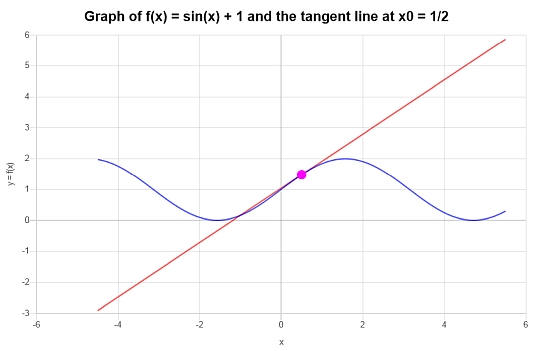
उदाहरण: स्पर्शरेखा रेखा समीकरण

फ़ंक्शन \(f(x) = \sin(x) + 1\)के लिए x = 1/2 पर स्पर्शरेखा रेखा क्या है?

Solution:

The following function has been provided: \(\displaystyle f(x)=\sin\left(x\right)+1\), for which we need to compute its derivative.

\( \displaystyle \frac{d}{dx}\left(\sin\left(x\right)+1\right)\)

By linearity, we know \(\frac{d}{dx}\left( \sin(x)+1 \right) = \frac{d}{dx}\left(\sin(x)\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)+\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \cos\left(x\right)\)

तमाम : हम पाते हैं कि बिंदु \(x_0 = \frac{1}{2}\) पर स्पर्शरेखा रेखा के संबंधित समीकरण द्वारा दिया गया है:

\[y = y_0 + f'(x_0)(x - x_0) \]

लेकिन इस विशिष्ट मामले में, \(\displaystyle y_0 = f(x_0)\), जिसका अर्थ है कि हमें फ़ंक्शन पर बिंदु \(x_0 = \frac{1}{2}\)के मूल्य में प्लग करने की आवश्यकता है, इसलिए हमें मिलता है:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

अब, व्युत्पन्न में भी ऐसा ही कर रहा है, \(x_0 = \frac{1}{2}\) के लिए हम पाते हैं

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

अब हमें केवल मूल्यों को प्लग करने की आवश्यकता है, इसलिए हम पाते हैं

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

तिहाई : हम पाते हैं कि इसी स्पर्शरेखा रेखा की हम तलाश कर रहे हैं, इसी बिंदु पर \(x_0 = \frac{1}{2}\) द्वारा दिया गया है

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

रेखांकन:

उदाहरण: एक और स्पर्शरेखा रेखा

फ़ंक्शन \(f(x) = \cos(x)\)के लिए x = 0 पर स्पर्शरेखा रेखा क्या है?क्या यह परिणाम समझ में आता है?

तमाम: उस \(f'(x) = -\sin(x)\)का निरीक्षण करें, तो फिर \(f'(0) = -\sin(0) = 0\)।यह है, स्पर्शरेखा रेखा में x = 0 पर m = 0 का ढलान है, इसलिए फिर स्पर्शरेखा रेखा का समीकरण केवल \(y = y_0 = \cos(0) = 1\)है।यह समझ में आता है क्योंकि इस मामले में, स्पर्शरेखा रेखा एक क्षैतिज रेखा है।

अधिक भेदभाव कैलकुलेटर

कुछ लोग दावा कर सकते हैं कि भेदभाव एक अपेक्षाकृत सीधा व्यायाम है, और यह कि एक का उपयोग करना वthaumaumaut r कैलकुलेटry आवश्यकता नहीं हो सकती है, लेकिन सच में, डेरिवेटिव की गणना अभी भी काफी बोझिल हो सकती है और लंबे समय तक आवश्यक हो सकती है अफ़रोट ।

जब आपके पास एक से अधिक चर के साथ एक अभिव्यक्ति होती है, तो व्युत्पन्न को खोजने के लिए आपको यह निर्धारित करने की आवश्यकता होगी कि क्या चर एक दूसरे से स्वतंत्र हैं, जिस स्थिति में आप उपयोग करते हैं आंशिक अवकलज , या यदि कोई समीकरण है जो चर को किस स्थिति में जोड़ता है, तो आपको उपयोग करने की आवश्यकता होगी अँगुला ।

अंतर पथरी में मुख्य दो क्षेत्र एकीकरण और भेदभाव हैं, और वे दोनों अपने व्यापक अनुप्रयोग हैं, हर जगह। आंशिक अवकलज इंजीनियरिंग और अर्थशास्त्र अनुप्रयोगों में बड़ी लंबाई में दिखाई देते हैं।

एक ओर, भेदभाव परिवर्तन की असीम दरों के साथ व्यवहार करता है, जबकि एकीकरण परिवर्तन की असीम दरों को समेटने के साथ संबंधित है, और admirably इसलिए, वे कसकर जुड़े हुए हैं सभा ।