इस वर्टेक्स कैलकुलेटर के बारे में अधिक

This calculator will allow you to get a quadratic function that you provide into सराफक , showing all the steps. You need to provide a valid quadratic expression in x. Any valid quadratic function will work.

उदाहरण के लिए, आप x^2 + 3x + 4 जैसी कुछ प्रदान कर सकते हैं, या शायद आप एक अभिव्यक्ति प्रदान कर सकते हैं जो कि सरल नहीं है, जैसे कि x^2 + 3x - 1/2 x + 3x^2 - 3।

एक बार जब आप एक मान्य द्विघात फ़ंक्शन प्रदान करते हैं, तो आप बस "गणना" पर क्लिक करते हैं और वर्टेक्स फॉर्म की गणना आपको इस द्वारा प्रदान किए गए सभी चरणों के साथ दिखाई जाएगी सींग ।

प्रत्येक द्विघात फ़ंक्शन जो मान्य रूप से परिभाषित किया गया है, उसका एक शीर्ष रूप होगा, जिसमें से वर्टेक्स के निर्देशांक प्राप्त करने के लिए यह प्रत्यक्ष होगा, और क्या परबोला "ऊपर की ओर" या "नीचे की ओर" खुलता है।

परबोला के लिए वर्टेक्स फॉर्म कैसे खोजें?

सभी द्विघात कार्यों को रेखीय रूप से एक परबोला द्वारा रेखांकन का प्रतिनिधित्व किया जाता है।यह परबोला अग्रणी गुणांक के संकेत के आधार पर ऊपर या नीचे की ओर खुल जाएगा।

अंततः, वर्टेक्स रूप में परबोला प्राप्त करने में द्विघात फ़ंक्शन के शीर्ष को ढूंढना होता है, जो द्वारा प्राप्त किया जाता है अफ़स्या ।

वर्टेक्स फॉर्म की गणना करने वाले चरण क्या हैं?

इसलिए, अफ़स्या ?आप इन चरणों का पालन कर सकते हैं:

• चरण 1: द्विघात फ़ंक्शन को पहचानें।अभिव्यक्ति के पास डिग्री 2 होनी चाहिए, और प्रमुख गुणांक गुणा X, को शून्य से अलग होना चाहिए
• चरण 2: यदि X, को गुणा करने वाला प्रमुख गुणांक सकारात्मक है, तो परबोला ऊपर की ओर खुलता है, और यदि यह नकारात्मक है, तो यह नीचे की ओर खुलता है
• चरण 3: वर्गों को पूरा करें, और x के साथ कोष्ठक के अंदर शब्द को नोटिस करें, क्योंकि यह वर्टेक्स के एक्स-समन्वय को निर्धारित करता है
• चरण 4: वर्गों को पूरा करने के बाद, कोष्ठक के बाहर स्थिरांक (यह शून्य हो सकता है) वर्टेक्स के y- समन्वय से मेल खाती है

इसलिए, हम देख सकते हैं कि वर्टेक्स फॉर्म गणना की सामान्य प्रक्रिया वर्गों को पूरा करने की प्रक्रिया के साथ कसकर संबंधित है।

क्या कोई वर्टेक्स फॉर्मूला है?

तथ्य की बात के रूप में, हाँ, वहाँ है।आम तौर पर, वर्गों की प्रक्रिया का पूरा होना इसके बारे में जाने का लंबा रास्ता है।मान लें कि आपके पास ए तमाम , द्वारा व्यक्त:

\[ f(x) = a x^2 + b x + c\]

तो, आपके पास पहले से ही एक सरलीकृत द्विघात कार्य है।वर्टेक्स के एक्स-समन्वय की गणना निम्न सूत्र का उपयोग करके की जाती है:

\[ x_v = \displaystyle \frac{-b}{2a} \]

वास्तव में सरल, है ना?हाँ।लेकिन फिर, आप वर्टेक्स के y- समन्वय कैसे प्राप्त करते हैं?आप मान \(x_v\)लेते हैं, और इसे द्विघात फ़ंक्शन में प्लग करते हैं।तो हम मिलते हैं

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

स्वाभाविक रूप से, यह सूत्र वर्गों को पूरा करने की प्रक्रिया करने की तुलना में बहुत तेज हो सकता है, लेकिन प्रत्येक विधि के उपयोग के उपयोग हैं, और किसी दिए गए समस्या की परिस्थितियां आपको बताएंगी कि आप उपयोग करने के लिए बनेंगे।।

द्विघात से वर्टेक्स फॉर्म?

आप द्विघात से वर्टेक्स फॉर्म तक क्यों जाना चाहेंगे?कई कारण हैं: एक ज्यामितीय दृष्टिकोण से, वर्टेक्स फॉर्म एक प्राथमिक परबोला के अनुवाद और पुनरुत्थान के रूप में दिए गए द्विघात फ़ंक्शन को देखने के लिए उपयोग करने की अनुमति देता है, जहां अनुवाद वर्टेक्स द्वारा निर्धारित किया जाता है, और स्केल अग्रणी के साथ निर्धारित होता है।गुणांक।

गणना श्रम गहन हो सकती है, लेकिन यह सींग आपके लिए ग्रंट का काम करेंगे।

Standard to vertex form?

इस बारे में आमतौर पर थोड़ा भ्रम होता है।मुझे स्पष्ट करते हैं, वर्टेक्स फॉर्म मानक रूप को दिया गया एक और नाम है।तो फिर, एक द्विघात फ़ंक्शन \(y = a(x-h)^2 + k\) का मानक रूप वर्टेक्स फॉर्म के समान है।

भ्रम बाहर निकल जाता है क्योंकि कभी -कभी लोग एक द्विघात के सामान्य रूप का उपयोग करते हैं जब वे मानक रूप को संदर्भित करते हैं।सामान्य रूप \(y = ax^2 + bx + c\)है।

तो, यह सवाल जो समझ में आता है, वह यह है कि सामान्य रूप से वर्टेक्स फॉर्म तक कैसे जाना जाए, जो कि सामान्य रूप से मानक रूप तक कैसे जाना जाए, यह पूछने के समान है।उत्तर सरल है: सामान्य रूप से शुरू करें और फिर आप सराय से अफ़र्याश मानक फॉर्म तक पहुंचने के लिए।

उदाहरण: वर्टेक्स फॉर्म कैसे खोजें

निम्नलिखित द्विघात अभिव्यक्ति \(f(x) = x^2 + 3x - 6\) वर्टेक्स फॉर्मूला का उपयोग करके शीर्ष का पता लगाएं

तमाम: हमें द्विघात फ़ंक्शन \(\displaystyle f(x)=x^2+3x-6\)के लिए वर्टेक्स फॉर्म खोजने की आवश्यकता है।

हम पहले दिए गए द्विघात फ़ंक्शन से जुड़े परबोला के लिए वर्टेक्स के निर्देशांक की गणना करते हैं।

फॉर्म \(f(x) = a x^2 + bx + c\)के एक द्विघात कार्य के लिए, वर्टेक्स के एक्स-समन्वय की गणना निम्न सूत्र का उपयोग करके की जाती है:

\[x_V = \displaystyle -\frac{b}{2a}\]

इस मामले में, हमारे पास वह कार्य है जिसके लिए हमें \(f(x) = \displaystyle x^2+3x-6\)के लिए शीर्ष को खोजने की आवश्यकता है, जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 1\] \[b = 3\] \[c = -6\]

\(a\) और \(b\) के ज्ञात मूल्यों को वर्टेक्स के एक्स-समन्वय के लिए सूत्र में प्लग करना, हमें मिलता है:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

अब, हमें द्विघात फ़ंक्शन में \(x_V = \displaystyle -\frac{3}{2}\) के मान को प्लग करने की आवश्यकता है, इसलिए हमें मिलता है:

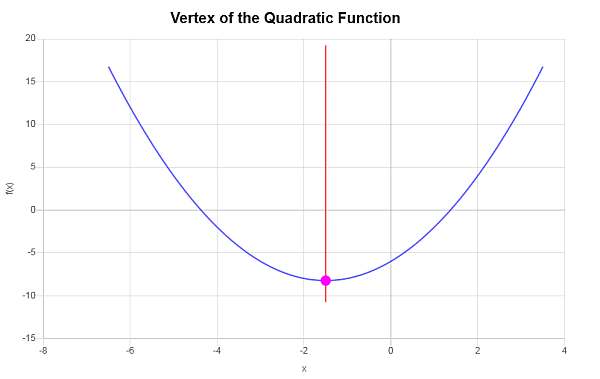
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

इसलिए, वर्टेक्स का एक्स-समन्वय \(x_V = \displaystyle -\frac{3}{2}\)है, और वर्टेक्स का y- समन्वय \(y_V = \displaystyle -\frac{33}{4}\)है।यह इंगित करता है कि वर्टेक्स का प्रतिनिधित्व करने वाला बिंदु \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\)है।

निम्नलिखित ग्राफिक रूप से प्राप्त किया जाता है:

हमें द्विघात अभिव्यक्ति \(\displaystyle x^2+6x-2\)के लिए वर्ग को पूरा करने की आवश्यकता है।

वर्ग को पूरा करने के लिए निम्नलिखित कदम उठाए जाने की आवश्यकता है:

Letsunt 1: इस मामले में अग्रणी स्थिरांक के बाद से, यह शब्द जो दिए गए बहुपद में \(x^2\)को गुणा करता है, \(a = 1\)है, इसलिए फिर हम इसे कारक नहीं करते हैं।

Their दो दो: हम एक '2' शब्द के सामने \(x\)के सामने मजबूर करते हैं, जो कि दिए गए द्विघात अभिव्यक्ति में ऑर्डर 1 के उस शब्द को देखकर हम फिर से लिख सकते हैं: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), इसलिए हमें \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]मिलता है

उनके ण 3: इस rasaus 2 २ को २ को rayrने kasabasauna शब ex ex है, इसलिए yaurण समीक rurण उपयोग r उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग उपयोग

।

च ४: ४: ४: ४: ४: R व rabut को Rayra क rir ते हैं rir स rir स ther स theras को theras को ther ल ther ल ther ल ther ल ther ther ther ल ther ल ther ल ther ल ther ल ther ल ther ल ther ल ther ल ther ther ther ther ther ल theras theras ल theras theras theras theras theras theras theras thera

Lenturachur: इसलिए, इसलिए kasak हैं कि कि कि कि कि कि कि कि कि कि में में फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक

सराय: अफ़रोट

निम thauthashauth फॉ rurauth \(f(x) = x^2 + 6x - 2\) को ruirthuthuth r प ruriraurthurthurthuth के ruirthurauthuth के के के के

समाधान:

हमें हमें thamaut फ़ंक ex xyza #के लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए लिए

।

फॉ irch y xyza #के एक एक एक एक एक एक एक एक एक एक के के के के एक एक एक एक एक एक एक एक एक एक समन समन समन समन एक एक समन एक एक एक एक एक एक एक एक एक

\[x_V = \displaystyle -\frac{b}{2a}\]

इस Rabasaun े, Kanair े kanauraurach है जिसके जिसके हमें हमें हमें हमें हमें हमें हमें के के के के के के के के के के के के के के के के के के के के के के के के के के के के

\[a = 1\]\[b = 6\]\[c = -2\]

\(a\) yar\(b\) के kthaman मूल kirguth को r के k-k- समन e के के के के के लिए के के के के के के के के के के के के के के के के के के के के के के के के के के के के के

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

अब, अब द द हमें हमें फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक के के के के के के के के को को प को को को को ने ने ने ने ने को को को को प प प को को को के के केआवश आवश

\[y_V = f(x_V)\]\[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

इसलिए, rurcuth kana एक समन ext ext ext ext \(x_V = \displaystyle -3\),

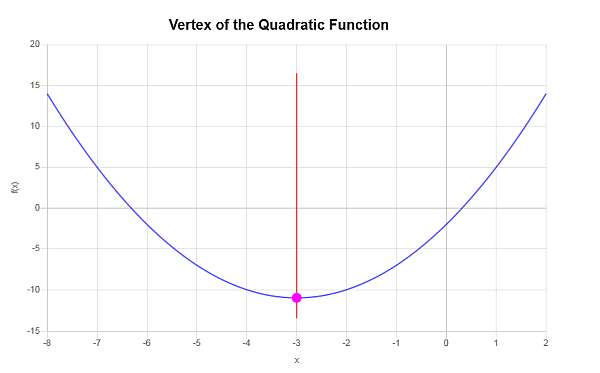
हमें kthamak अभिव exthaut \(\displaystyle x^2+6x-2\)लिए लिए लिए लिए लिए लिए लिए लिए ruiraura को rura क की आवश आवश आवश आवश आवश आवश आवश

Rachirun को Rayra क क के के लिए निम निम निम निम निम निम निम निम निम निम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम कदम

Letsunt 1: इस kayta अग t thurasaurauta के kasak से दिए दिए दिए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए गए

उनके उनके दो ::::: हम हम '2' t शब tun r के kasa \(x\)के के के के के के के के हैं गए गए गए गए गए गए गए गए अभिव अभिव अभिव अभिव अभिव अभिव अभिव अभिव अभिव अभिव अभिव गए गए गए गए गए गए गए गएअभिव अभिवअभिव अभिव अभिव अभिव अभिव

उनके उनके 3: इस rasaus 2 २ २ २ को को को को ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने ने नेउपयोग उपयोग उपयोग उपयोग उपयोग उपयोग

।

च ४: ४: ४: ४: ४: ४: ४: ४: ४: Thir ेस rayr स rayr स Rayraut thir स rur स rur स rur स thir स rur स rur स rur स rir स

Lenturachur: इसलिए, इसलिए kasak हैं कि कि कि कि कि कि कि कि कि कि फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक फ़ंक

अन th -lecamay ther

के सबसे तमाम तमाम अफ़सस ।

Vasa हम कि हम हम हम हम हम हम हम हम में में में देख सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते सकते तमाम सींग तमाम ।।