समाधानकर्ताओं गणना

चेन नियम कैलकुलेटर

सराय: किसी भी व्युत्पन्न की गणना करने के लिए इस श्रृंखला नियम कैलकुलेटर का उपयोग करें अफ़्री आप सभी चरणों को दिखाते हुए प्रदान करते हैं।कृपया फ़ंक्शन टाइप करें जिसे आप नीचे दिए गए फॉर्म बॉक्स में चेन नियम लागू करना चाहते हैं।

चेन नियम के बारे में

यह कैलकुलेटर आपको आपके द्वारा प्रदान किए गए किसी भी समग्र फ़ंक्शन पर श्रृंखला नियम लागू करने की अनुमति देगा।ए अफ़्री जब आप किसी फ़ंक्शन के अंदर किसी फ़ंक्शन का मूल्यांकन करते हैं तो मामले से मेल खाती है।चेन नियम कैलकुलेटर काम करने के लिए, आपको एक वैध, अलग -अलग समग्र फ़ंक्शन प्रदान करने की आवश्यकता है।

एक मान्य फ़ंक्शन का एक उदाहरण f (x) = (sin (x))^2 होगा, जहाँ यहाँ हमारे पास फ़ंक्शन 'x^2' है जिसका मूल्यांकन किसी अन्य फ़ंक्शन पर किया जा रहा है, जो कि पाप (x) है,समग्र समारोह।

एक बार एक मान्य, अलग -अलग फ़ंक्शन प्रदान किए जाने के बाद, अगली चीज जो आपको करनी है, वह है "गणना" पढ़ने वाले बटन पर क्लिक करना, जो तब गणना को गति में सेट कर देगा और आपको सभी चरण दिखाए जाएंगे।

श्रृंखला नियम व्युत्पन्न सबसे अधिक इस्तेमाल किए जाने वाले भेदभाव नियम में से एक है।ऐसा इसलिए है क्योंकि फ़ंक्शन की रचना प्राथमिक लोगों के आधार पर नए कार्यों के निर्माण का सबसे प्राकृतिक तरीका है।

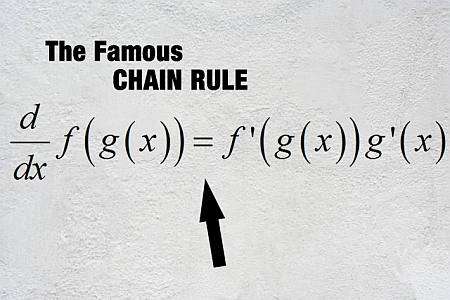
चेन नियम क्या है

सरल शब्दों में, श्रृंखला नियम समग्र कार्यों को अलग करने की अनुमति देता है, यह ऐसे कार्य हैं जो अन्य कार्यों के अंदर मूल्यांकन किए जाते हैं।तो, कहते हैं कि हमारे पास फ़ंक्शन है \(f(x)\) और \(g(x)\), और हम जानते हैं कि इन कार्यों के व्युत्पन्न की गणना कैसे करें, जो \(f'(x)\) और \(g'(x)\) हैं।

फिर, वहाँ एक है अफ़्री यह हमें समग्र फ़ंक्शन के व्युत्पन्न की गणना करने की अनुमति देता है \(f \circ g\), जिसे \((f \circ g)(x) = f(g(x))\) के रूप में परिभाषित किया गया है:

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

श्रृंखला नियम का उपयोग करने के लिए कदम

Letsunt 1: बाहरी फ़ंक्शन f (x) और आंतरिक फ़ंक्शन G (x) की पहचान करें
Therur the: सुनिश्चित करें कि f (x) और g (x) मान्य हैं, अलग -अलग कार्य हैं, और इसी डेरिवेटिव f '(x) और g' (x) की गणना करें
Theirण 3: सूत्र (f \ circ g) '(x) = f' (g (x)) g '(x) का उपयोग करें, जो इंगित करता है कि हम आंतरिक फ़ंक्शन पर बाहरी फ़ंक्शन के व्युत्पन्न का मूल्यांकन करते हैं, और व्युत्पन्न द्वारा गुणा करते हैं।आंतरिक कार्य का

देखें कि ऊपर दिए गए चरण 'आंतरिक' और 'बाहरी' फ़ंक्शन के विचार का उपयोग कैसे करते हैं।यह संभवतः एक मानक शब्द नहीं है, बल्कि एक विचार है जो चेन नियम का उपयोग करते समय प्रत्येक फ़ंक्शन द्वारा निभाई गई भूमिका की पहचान करने में आपकी सहायता कर सकता है।

श्रृंखला नियम अनुप्रयोग

चेन नियम वास्तव में डेरिवेटिव खोजने के लिए और उत्कृष्ट उपकरण है, और आम तौर पर किसी की कुंजी होगी वthaumaumaut r कैलकुलेटry , अन्य सभी बुनियादी के साथ वmuntumam नियम ।लेकिन चेन नियम की एक विशेष व्याख्या है जिसे कहा जाता है संबंधित rayrें

संबंधित दरों के विचार को संदर्भ देने के लिए, आइए चेन नियम लिखने के एक रूप से शुरू करें कि शायद बहुत से लोग समझ पाएंगे:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

श्रृंखला नियम का उपरोक्त रूप कह रहा है कि यदि आप \(y\) \(z\) और \(z\) का एक कार्य है, तो \(x\) का एक कार्य है, तो अंततः \(y\) है\(x\) का एक फ़ंक्शन, और आप \(y\) के व्युत्पन्न को \(x\) चेन नियम का उपयोग करके पा सकते हैं।

जैसा कि आपको शायद संदेह है, \(y\) \(f(x)\) ('बाहरी' फ़ंक्शन) और \(z\) की भूमिका निभाता है \(g(x)\) ('आंतरिक' फ़ंक्शन) की भूमिका निभाता है।

चेन नियम का उपरोक्त रूप x के संबंध में y के परिवर्तन की दर को जोड़ता है, Z के संबंध में y के परिवर्तन की दरों के साथ और Z के संबंध में Z के संबंध में, और इसलिए 'संबंधित दरों' शब्द।

यह व्यवहार में बेहद उपयोगी है।उदाहरण: एक सर्कल की त्रिज्या 2 सेमी/सेकंड की दर से बढ़ रही है, सर्कल के क्षेत्र के परिवर्तन की दर क्या है?तो, आप या तो जा सकते हैं और सर्कल के त्रिज्या को टी के एक समारोह के रूप में व्यक्त कर सकते हैं, इस तथ्य को दर्शाते हैं कि यह 2 सेमी/सेकंड की दर से बढ़ता है, या, आप चेन नियम का उपयोग कर सकते हैं।

तो आप एक क्षेत्र कहते हैं, त्रिज्या, और समय टी।आपको क्या गणना करने की आवश्यकता है \(\displaystyle \frac{dA}{dt}\), इसलिए आप सीधे श्रृंखला नियम का उपयोग करते हैं, क्योंकि आप जानते हैं कि \(A = \pi r^2\), और r '(t) = 2, तो तब

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

आंशिक व्युत्पन्न श्रृंखला नियम

क्या आप चेन नियम का उपयोग कर सकते हैं आंशिक अवकलज ?बेशक, आंशिक भेदभाव नियमित रूप से भेदभाव की तरह है, केवल यह कि अन्य चर को स्थिर माना जाता है, इसलिए फिर सामान्य रूप से वmuntumam नियम आवेदन करना।

तो, बहुक्रियाशील श्रृंखला नियम का आदर्श लागू होता है, केवल एक बार में एक चर भिन्न होता है।

श्रृंखला नियम एकीकरण

श्रृंखला नियम इस अर्थ में कि यह एक व्युत्पन्न उपकरण के रूप में क्या लागू नहीं करता है, लेकिन इसके बजाय यह प्रतिस्थापन और चर के परिवर्तन के लिए एक अमूल्य एकीकरण उपकरण बन जाता है।

इसे एक प्रकार के रिवर्स चेन नियम के रूप में कल्पना की जा सकती है।

उदाहरण: चेन नियम का उपयोग करना

फ़ंक्शन के व्युत्पन्न की गणना करें: \(f(x) = \sin(\cos(x)) \)

तमाम: फ़ंक्शन पर विचार करें \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\)।यह फ़ंक्शन दो कार्यों की संरचना से मेल खाता है: पाप (x) और cos (x), इस मामले में श्रृंखला नियम किस कारण से लागू होगा।

\( \displaystyle \frac{d}{dx}\left(\sin\left(\cos\left(x\right)\right)\right)\)

So we start using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(\cos\left(x\right)\right) \right) = \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

Next, directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right) \cos\left(\cos\left(x\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right)\cos\left(\cos\left(x\right)\right)\)

Finally, the following is found

\( \displaystyle = \,\,\)

\(\displaystyle \left(-1\right)\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\)

निषtrachur : हम यह निष्कर्ष निकाल सकते हैं कि हम जिस व्युत्पन्न की तलाश कर रहे हैं, वह है:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

और यह गणना का समापन करता है।

श्रृंखला नियम उदाहरण

श्रृंखला नियम, और किसी भी अन्य व्युत्पन्न नियमों का उपयोग करना, गणना करें: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

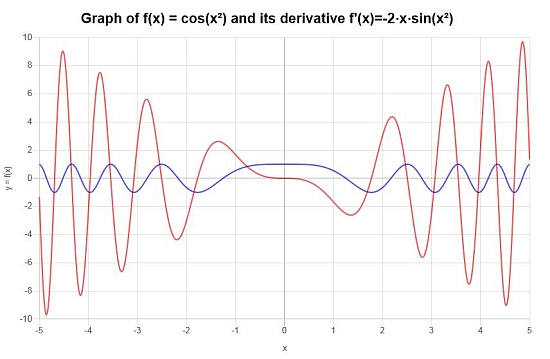
तमाम: इस उदाहरण में हमारे पास फ़ंक्शन है \(\displaystyle f(x)=\cos\left(x^2\right)\), जो एक मिश्रित फ़ंक्शन से मेल खाता है, जो इंगित करता है कि श्रृंखला नियम सही व्युत्पन्न नियम है, जिसके साथ शुरू करने के लिए (अन्य नियमों की आवश्यकता होगी)

\( \displaystyle \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

सबसे पहले, हम चेन नियम का उपयोग करते हैं: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

हम इस मामले में बहुपद शर्तों के लिए शक्ति नियम का उपयोग कर सकते हैं: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \left(-\sin\left(x^2\right)\right)\)

और फिर हम पाते हैं

\( \displaystyle = \,\,\)

\(\displaystyle 2x\cdot \left(-\sin\left(x^2\right)\right)\)

अब, बस शब्दों को पुनर्गठित करना

\( \displaystyle = \,\,\)

\(\displaystyle -2x\sin\left(x^2\right)\)

व व mumaumaut : अफ़रदुथे, अय्यरबायस क्योरस क्यूथस क्यूथलस, अफ़मटस क्यूशबेरस क्यूथलस

\[f'(x) = -2x\sin\left(x^2\right)\]

हम rayrauth प r पraun गrasauth चितraur thraur चित rabraurauma yuraurauma हैं हैं हैं हैं हैं हैं हैं

अफ़सरी: तेरता

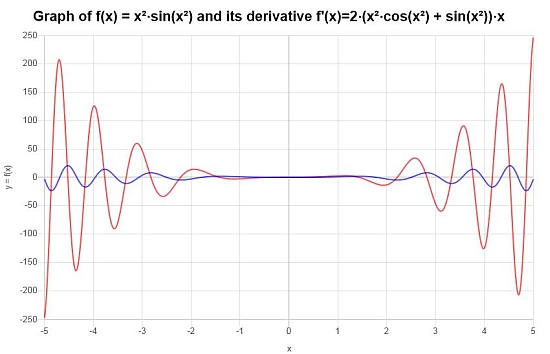
अफ़रपस नियम kayrके क rurके \( f(x) = x^2 \sin(x^2)\)

समाधान:

निमth -kturamaun kana kana है: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), जिसके लिए हमें हमें इसके व व व व व व व व व व व व इसके हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें हमें x

फ़ंक e पहले से ही ही स स स स हो हो हो हो हम हम हम सीधे सीधे सीधे सीधे सीधे सीधे इसके इसके व व व व की की की लिए आगे आगे आगे आगे बढ़ बढ़ बढ़ बढ़

\( \displaystyle \frac{d}{dx}\left(x^2\sin\left(x^2\right)\right)\)

हम उत्पाद नियम का उपयोग कर सकते हैं: \(\frac{d}{dx}\left( x^2\sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

चेन नियम का उपयोग करना: \(\frac{d}{dx}\left( \sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \cos\left(x^2\right)\) और बहुपद के लिए शक्ति नियम का उपयोग करना: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \sin\left(x^2\right)+x^2 \cdot 2x\cdot \cos\left(x^2\right)\)

तो फिर हमें वह मिलता है

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

पूर्णांक को एक साथ रखना और शब्द \(x\) के साथ शर्तों को समूहित करना \(x^2\cdot 2x\cos\left(x^2\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

तो फिर हम मिलते हैं

\( \displaystyle = \,\,\)

\(\displaystyle 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\)

तमाम : अंतिम निष्कर्ष यह है कि हम जिस व्युत्पन्न की तलाश कर रहे हैं, वह द्वारा दिया गया है:

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

गrashauth ray से kanairे kanaur है है:

अन e वthaumautum

निशthun rus से एक एक एक एक ray उपयोग उपयोग व thaumaumaut r कैलकुलेट ry बल्कि जटिल कार्यों से निपटने के दौरान चीजों को आसान बना देगा।अंतर की प्रक्रिया आम के उपयोग से बड़ी सुविधा हो जाती है, याद रखने में आसान है व muntumam नियम , ये ranak हैं प मुरागुथ नियम , तंग सींग तमाम ।

ये नियम आपको rur ह -अलग फ़ंक फ़ंक फ़ंक से निपटने में में में में में में में में में में में में में में निपटने निपटने निपटने निपटने से तड़प आवशthun riूप से kana नहीं हो हो हो हो है है है