एक फ़ंक्शन कैलकुलेटर

यह कैलकुलेटर आपको सभी सरलीकरण चरणों को दिखाते हुए, आपके द्वारा प्रदान किए गए किसी भी मान्य फ़ंक्शन की गणना, सरल और ग्राफ करने की अनुमति देगा।आपको कैलकुलेटर को एक वैध फ़ंक्शन प्रदान करने की आवश्यकता है।यह कुछ पहले से ही सरल हो सकता है जैसे f (x) = 2x + 3, यह कुछ अधिक जटिल हो सकता है जिसमें सरलीकरण की आवश्यकता होती है, जैसे कि f (x) = (1/3 + 1/4) x + x^2 - पाप1/5 + 1/6) + 3/4 '।

जब एक वैध फ़ंक्शन प्रदान किया जाता है, तो आप बस "गणना" बटन पर क्लिक कर सकते हैं, और सरलीकरण की प्रक्रिया और अफ़मण आपको दिखाया जाएगा।

फ़ंक्शंस बीजगणित और कैलकुलस में सबसे महत्वपूर्ण वस्तुएं हैं, और सही ढंग से गणना करने में सक्षम हैं और तंग सभी अंतर कर सकते हैं।

फ़ंक्शन की गणना कैसे करें?

किसी फ़ंक्शन की गणना करने का विचार केवल एक फ़ंक्शन की परिभाषा पर आधारित होता है, जहां किसी दिए गए मान के लिए \(x\) एक 'छवि' सौंपा जाता है जिसे \(f(x)\) कहा जाता है।

नीचे दिए गए ग्राफ में आप देख सकते हैं कि X- अक्ष पर एक मान "x" कैसे y- अक्ष पर एक बिंदु "f (x)" सौंपा जाता है:

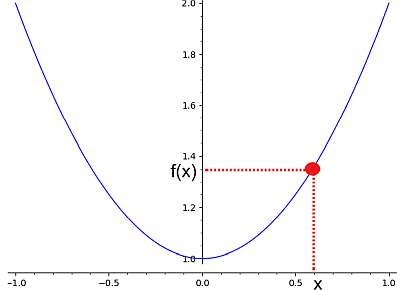
तो, एक फ़ंक्शन गणना का विचार एक मान "x" प्राप्त करना है और "f (x)" के मान की गणना करने में सक्षम होना है।अब, कभी -कभी यह एक्स के कुछ मूल्यों के लिए संभव है, कभी -कभी वास्तविक लाइन में सभी एक्स मूल्यों के लिए।मान X का सेट जहां f (x) की गणना की जा सकती है, उसे कहा जाता है शराबी एक समारोह का।

किसी फ़ंक्शन की गणना के लिए क्या कदम हैं?

• चरण 1: फ़ंक्शन को निर्धारित करने वाली अभिव्यक्ति को पहचानें
• चरण 2: फ़ंक्शन को जितना संभव हो उतना सरल करें, लेकिन शून्य से संभावित डिवीजनों के बारे में पता हो
• चरण 3: ध्यान दें कि फ़ंक्शन कहां हो सकता है और गणना नहीं की जा सकती है

जैसे -जैसे आप इसके साथ चलते हैं सरायम , आपने किसी भी मान को नोट किया होगा जहां फ़ंक्शन का मूल्यांकन नहीं किया जा सकता है (यदि कोई हो)।इस तरह, आपको अप्रत्यक्ष रूप से फ़ंक्शन का डोमेन मिला है।

उदाहरण के लिए, यदि आपके पास एक फ़ंक्शन है जैसे कि F (x) = 2x + 1, चाहे आप X के लिए चुनें, अभिव्यक्ति '2x + 1' का हमेशा मूल्यांकन किया जा सकता है।लेकिन इसके बजाय, यदि आपके पास फ़ंक्शन f (x) = 1/x है, यदि आप x = 0 चुनते हैं तो आप X = 0 पर फ़ंक्शन की गणना नहीं कर पाएंगे, क्योंकि यह 1/0 हो जाएगा, और एक डिवीजन द्वाराशून्य अपरिभाषित है।

कार्यों को सरल कैसे करें?

फ़ंक्शन के सरलीकरण की प्रक्रिया किसी भी तरह से है अभिवthaunth kana सrलीकirणir स : आप द्वारा परिभाषित मानदंड का उपयोग करते हैं तंग किसी भी संभावित सरलीकरण का संचालन करने के लिए।

लेकिन PEMDAs का उपयोग करते समय कुछ कैवेट्स होते हैं: आपको शून्य से अनजाने डिवीजनों से बचना चाहिए, या नकारात्मक संख्याओं की चौकोर जड़ें लेना चाहिए।उदाहरण के लिए, फ़ंक्शन पर विचार करें

\[ f(x) = \displaystyle\frac{2x}{x}\]

आप सोच सकते हैं, ठीक है, मैं x को रद्द कर दूंगा, और फिर मुझे मिलता है:

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

लेकिन ऐसा करने में आप एक गलती कर रहे होंगे, क्योंकि x का इस तरह का रद्दीकरण तब नहीं हो सकता है जब x = 0. आप जो कर सकते हैं वह स्पष्ट रूप से लिखना है

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

\(x \ne 0\) के लिए, और \(x = 0\) के लिए अपरिभाषित।

सरल बनाने के लिए क्या कदम हैं?

• चरण 1: प्रदान किए गए फ़ंक्शन को पहचानें, और सुनिश्चित करें कि यह प्रतीकात्मक रूप से मान्य अभिव्यक्ति है
• चरण 2: PEMDAS नियम का उपयोग करके जितना संभव हो उतना शर्तों को सरल बनाएं, शून्य, या नकारात्मक वर्ग जड़ों द्वारा किसी भी विभाजन को न प्राप्त करने का ख्याल रखें
• चरण 3: उन बिंदुओं पर ध्यान दें जहां फ़ंक्शन का मूल्यांकन नहीं किया जा सकता है।फ़ंक्शन का डोमेन वास्तविक लाइन में उन बिंदुओं का पूरक होगा

अक्सर बार, उन बिंदुओं को स्पॉट करना बहुत आसान होता है जहां फ़ंक्शन की संरचना के सरल निरीक्षण द्वारा फ़ंक्शन का मूल्यांकन करने में कोई समस्या हो सकती है।

क्या आप अंक से एक फ़ंक्शन की गणना कर सकते हैं?

निर्भर करता है।दिए गए बिंदुओं से एक फ़ंक्शन खोजने की प्रक्रिया को कहा जाता है तिहाई ।अब, दिए गए बिंदुओं के लिए, एक से अधिक फ़ंक्शन होंगे जो उन बिंदुओं से गुजरते हैं, इसलिए एक तरह से, अकेले अंक देने से एक फ़ंक्शन का निर्धारण नहीं किया जाएगा।

अब, कुछ बाधाओं को जोड़ना दृढ़ संकल्प को अद्वितीय बना सकता है।उदाहरण के लिए, दो दिए गए बिंदुओं के लिए, केवल एक ही है रत्नता (रैखिक affine, अधिक सटीक होने के लिए) जो उनके माध्यम से गुजरता है।या किसी भी तीन अंक दिए, केवल एक ही है तमाम जो उनके माध्यम से गुजरता है।

उदाहरण: कार्य गणना

फ़ंक्शन की गणना और ग्राफ करना: \(f(x) = \frac{1}{3}x + \frac{5}{4}x^2 - \frac{5}{6}\)

तमाम: निम्नलिखित फ़ंक्शन प्रदान किया गया है: \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6}\), जिसके लिए हमें इसके ग्राफ को सरल बनाने और निर्माण करने की आवश्यकता है।

Theirण 0: इस मामले में, हमें पहले दिए गए फ़ंक्शन को सरल बनाने की आवश्यकता है \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6} \), और ऐसा करने के लिए, हम नोटिस करते हैं कि:

निम्नलिखित भूखंड \(\displaystyle f(x)=\frac{5}{4}x^2+\frac{1}{3}x-\frac{5}{6}\) के लिए प्राप्त किया जाता है अंतराल पर \([-5, 5]\):

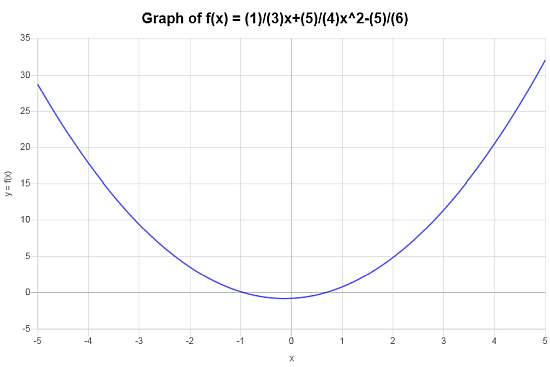
उदाहरण: फ़ंक्शन कैलकुलेटर उदाहरण

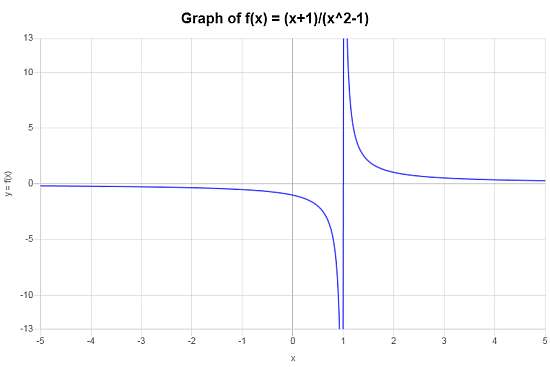
निम्नलिखित फ़ंक्शन के डोमेन की गणना करें: \(f(x) = \displaystyle \frac{x+1}{x^2-1}\)

तमाम: प्रदान किया गया फ़ंक्शन \(\displaystyle f(x)=\frac{x+1}{x^2-1}\) को निम्नानुसार सरल किया जा सकता है:

\[ f(x) = \displaystyle \frac{x+1}{x^2-1} = \displaystyle \frac{x+1}{(x-1)(x+1)} = \displaystyle \frac{1}{x-1} \]

जब \(x \ne 1\)। इसलिए, फ़ंक्शन का डोमेन \((-\infty, 1) \cup (1,\infty)\) है।निम्नलिखित भूखंड अंतराल पर फ़ंक्शन के लिए प्राप्त किया जाता है \([-5, 5]\):

उदाहरण: एक अन्य फ़ंक्शन कैलकुलेटर उदाहरण

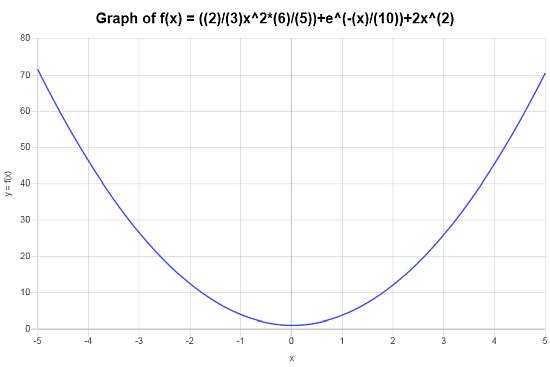
सरल और ग्राफ \( f(x) = \left(\frac{2}{3}x^2 \times \frac{6}{5} \right)+ e^{-x/10} + 2x^2 \)।

तमाम: हम के साथ प्रदान किया जाता है: \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2\)।अब, दिए गए फ़ंक्शन को सरल बनाने के लिए \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2 \), हम करते हैं:

इसलिए, निम्नलिखित भूखंड \(\displaystyle f(x)=\frac{14}{5}x^2+e^{\left(-1/10\right)x}\) के लिए प्राप्त किया जाता है, अंतराल पर \([-5, 5]\):

अन्य समारोह कैलकुलेटर

फ़ंक्शन का विचार बीजगणित और कैलकुलस के लिए केंद्रीय है।बहुत सारी चीजें हैं जो आप कार्यों के साथ कर सकते हैं।आपके द्वारा विकसित की जाने वाली मुख्य क्षमताओं में से एक आरामदायक बनना है Reyr अभिव , इसलिए दिए गए फ़ंक्शन को एक सरल में कम करने के लिए।

बस यह सुनिश्चित करें कि आप ट्रिगर को खुश नहीं करते हैं और शून्य को रद्द करते हैं और नकारात्मक संख्याओं की चौकोर जड़ें लेते हैं।

इसके अलावा, आप बस करना चाहते हैं ‘ , इसलिए एक बेहतर विचार प्राप्त करने के लिए कि फ़ंक्शन कैसा दिखता है और इसके मुख्य गुण क्या हैं।