समाधानकर्ताओं गणना

विभेदक कैलकुलेटर

सराय: इस विभेदक कैलकुलेटर का उपयोग करें, आपके द्वारा दिए गए किसी फ़ंक्शन के अंतर को खोजने के लिए, दिए गए बिंदु पर जो आप प्रदान करते हैं, सभी चरणों को दिखाते हैं।कृपया नीचे दिए गए फॉर्म बॉक्स में फ़ंक्शन और बिंदु टाइप करें।

विभेदक कैलकुलेटर

यह कैलकुलेटर आपको आपके द्वारा प्रदान किए गए एक फ़ंक्शन के अंतर की गणना करने की अनुमति देगा, जो आप प्रदान करते हैं, प्रक्रिया के सभी चरणों को दिखाते हैं।

आपके द्वारा प्रदान किया जाने वाला फ़ंक्शन किसी भी मान्य विभाज्य फ़ंक्शन जैसे f (x) = x^2 + 2x, या f (x) = x^2*sin (x) हो सकता है, बस दो उदाहरणों का उल्लेख करने के लिए।

फिर, जब आपने अंतर गणना के लिए फ़ंक्शन और बिंदु प्रदान किया है, तो केवल "गणना" पर क्लिक करें ताकि दिखाए गए प्रक्रिया के सभी चरणों को प्राप्त करें।

के विचार गरम स्पर्शरेखा रेखा के साथ कसकर है और रोटी , जैसा कि अंतर ठीक से y की भिन्नता को माप रहा है, साथ तमाम दिए गए बिंदु पर।

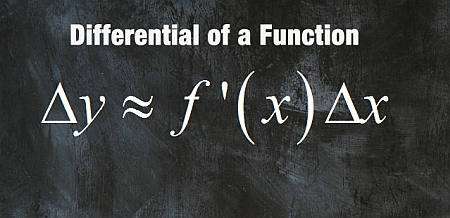
एक अंतर क्या है?

विभेदक कैलकुलस में, विचार यह है कि डेरिवेटिव आपको किसी दिए गए बिंदु पर किसी फ़ंक्शन के परिवर्तन की तत्काल दर के बारे में जानकारी देते हैं।

अंतर की अवधारणा का उपयोग करता है सराफक किसी दिए गए बिंदु पर व्युत्पन्न द्वारा निर्धारित \(x_0\) इसके द्वारा फ़ंक्शन के व्यवहार को अनुमानित करने के लिए तमाम ।

अंतर का सूत्र इस विचार पर आधारित है कि

\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]

जहां \(\Delta y = y - f(x_0)\) और \(\Delta x = x - x_0\)अंतर के लिए \(dy\), हम परिभाषित करते हैं

\[\displaystyle dy = f'(x_0) dx \]

यह (ढीला) परिभाषा इस विचार पर आधारित है कि रैखिक सन्निकटन और फ़ंक्शन एक ही व्यवहार के लिए दृष्टिकोण है जब \(x\) पर्याप्त रूप से \(x_0\) के करीब है।

एक अंतर की गणना के लिए कदम

Letsunt 1: फ़ंक्शन f (x) और बिंदु X0 को पहचानें जिस पर आप अंतर की गणना करना चाहते हैं
Therur the: व्युत्पन्न f '(x) की गणना करें और X0 पर इसका मूल्यांकन करें, ताकि आप F' (x0) प्राप्त करें।जरूरत पड़ने पर इसे सरल बनाएं
Theirण 3: सूत्र का उपयोग करें \(\displaystyle dy = f'(x_0) dx \)

कभी -कभी आपको \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \) के रूप में लिखा गया अंतर मिलेगा, यह दर्शाता है कि आप y में परिवर्तनों का अनुमान लगाने के लिए अंतर का उपयोग करेंगे, जिसे \(\Delta y\) द्वारा मापा जाता है।

विभेदक कैलकुलेटर डाई

इसका उपयोग करना विभेदक कैलकुलेट व्युत्पन्न की गणना की प्रक्रिया के साथ आपको समय बचा सकते हैं।अंतर का विचार हमेशा एक अजीब रहा है, इस अर्थ में कि यह शिथिल रूप से परिभाषित प्रतीत होता है।

यद्यपि अंतर को परिभाषित करने और उनके संचालन को औपचारिक रूप से परिभाषित करने का एक तरीका है (एक विषय जिसे विभेदक रूप कहा जाता है), अधिकांश गणितज्ञों को अंतर के लिए एक कारण नहीं दिखता है, क्योंकि उनकी कोई नई जानकारी प्रदान नहीं करती है जो व्युत्पन्न या पहला आदेश सन्निकटन हैप्रदान नहीं करते हैं।

कुल विभेदक व्याख्या

अंतर का सबसे आम अनुप्रयोग और व्याख्या जब इसकी 'परिमित' अभिव्यक्ति में उपयोग की जाती है:

\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]

जहां आप y में भिन्नता का अनुमान लगाना चाहते हैं, जैसा कि \(\Delta y\) द्वारा मापा जाता है, x में भिन्नता से, जैसा कि \(\Delta x\) द्वारा मापा जाता है और बिंदु पर व्युत्पन्न।

कभी -कभी यह \(\Delta y\) कहा जाता है अयस्क या कुल अंत ।

युक्तियाँ और चालें

यह मत भूलो कि अंतर को एक सैद्धांतिक परिभाषा के रूप में लिया जा सकता है, \(\displaystyle dy = f'(x_0) dx \), जो x में एक infinitesimal भिन्नता द्वारा y कारण में infinitesimal भिन्नता को इंगित करता है।

इसका उपयोग इसके कुल अंतर के रूप में भी किया जा सकता है, जिसमें आपके पास है

\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]

जो आपको y में एक अनुमानित भिन्नता बताता है, जब x में परिवर्तन के लिए (\(x_0\) से \(x\))।

सभी बीजगणितीय कैलकुलेटर का केंद्र बुनियादी संख्याओं की शक्ति के साथ शुरू होता है।

उदाहरण: विभेदक कैलकुलेटर

फ़ंक्शन पर विचार करें: \(f(x) = x^2\)।बिंदु पर इसका अंतर खोजें \(x_0 = 1\)।

तमाम: इस पहले उदाहरण के मामले में, हम फ़ंक्शन \(\displaystyle f(x)=x^2\) के साथ काम करते हैं, जिसके लिए हमें बिंदु पर इसके अंतर की गणना करने की आवश्यकता है \(x_0 = 1\)।

फ़ंक्शन पहले से ही सरल हो गया, इसलिए हम सीधे इसके व्युत्पन्न की गणना करने के लिए आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(x^2\right)\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x\)

गरम : फ़ंक्शन के लिए अंतर के लिए सूत्र \(\displaystyle f(x)=x^2\) बिंदु पर \(x_0 = 1\) है:

\[dy = f'(x_0)(x - x_0) \]

हम \(\displaystyle y_0 = f(x_0)\) को परिभाषित करते हैं, इसलिए फ़ंक्शन में POINT \(x_0 = 1\) का मान प्लग करना होता है:

\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]

इसके अलावा, गणना की गई व्युत्पन्न के लिए बिंदु \(x_0 = 1\) के मान को प्लग करना:

\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]

तो, अब हम इस मान को प्राप्त करने के लिए अंतर सूत्र में प्लग करते हैं:

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]

तिहाई : इसलिए, हम पाते हैं कि फ़ंक्शन के लिए अंतर \(\displaystyle f(x)=x^2\) बिंदु पर \(x_0 = 1\) है:

\[dy = 2x-2 \]

उदाहरण: विभेदक गणना

दिए गए फ़ंक्शन के लिए: \(f(x) = x^3 + 3x^2 - 2\), बिंदु पर अंतर खोजें \(x_0 = 2\)।

तमाम: अब, हमें जिस कार्य के लिए अंतर खोजने की आवश्यकता है वह \(\displaystyle f(x)=x^3+3x^2-2\) है,

\( \displaystyle \frac{d}{dx}\left(x^3+3x^2-2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3+3x^2-2 \right) = \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2\right)\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+3 \cdot 2x\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+3\cdot 2x\)

We reduce the integers that can be multiplied: \(\displaystyle 3\times2 = 6\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+6x\)

Directly reorganizing/simplifying/expanding

\( \displaystyle = \,\,\)

\(\displaystyle 3\left(x+2\right)x\)

अफ़रोट : हम उस अंतर के लिए निम्न सूत्र का उपयोग करते हैं जो हमें दिए गए फ़ंक्शन के लिए निर्माण करने की आवश्यकता है \(\displaystyle f(x)=x^3+3x^2-2\), दिए गए बिंदु पर \(x_0 = \frac{1}{2}\) है:

\[dy = f'(x_0)(x - x_0) \]

उस \(\displaystyle y_0 = f(x_0)\) का निरीक्षण करें, जिसका अर्थ है कि \(x_0 = \frac{1}{2}\) पर फ़ंक्शन का मूल्यांकन करना हम पाते हैं:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]

फिर, हम बिंदु पर व्युत्पन्न प्राप्त करते हैं \(x_0 = \frac{1}{2}\):

\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]

इसलिए, हम निम्नलिखित प्राप्त करते हैं

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]

तिहाई : अंतिम निष्कर्ष यह है कि हम जिस अंतर की तलाश कर रहे हैं, वह द्वारा दिया गया है:

\[dy = \frac{15}{4}x-\frac{15}{8} \]

विभेदक उदाहरण

हमें फ़ंक्शन दिया गया है: \(f(x) = \frac{\sin(x)}{x}\)।बिंदु पर इसका अंतर खोजें \(x_0 = \frac{\pi}{2}\)।

समाधान:

निम्नलिखित फ़ंक्शन प्रदान किया गया है: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), जिसके लिए हमें बिंदु पर इसके अंतर की गणना करने की आवश्यकता है \(x_0 = \frac{\pi}{2}\)।

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}\)

So then after simplifying:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}\)

तंग : अब यह दिए गए बिंदु के लिए \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) से जुड़े अंतर को खोजने का समय है, \(x_0 = \frac{\pi}{2}\)।उपयोग किया जाने वाला सूत्र है:

\[dy = f'(x_0)(x - x_0) \]

हम गणना किए गए व्युत्पन्न में बिंदु \(x_0 = \frac{\pi}{2}\) का मान प्लग करते हैं, जिसके लिए होता है:

\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]

इसलिए, अंतर सूत्र का उपयोग करना:

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

तिहाई : इसी अंतर है:

\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

अन्य भेदभाव कैलकुलेटर

सराय एक प्रश्न के बिना कैलकुलस में एक प्रमुख तत्व है।डेरिवेटिव समझने के लिए आवश्यक जानकारी प्रदान करते हैं सराफक कार्यों की।जैसा कि उन लोगों का अंतरंग संबंध है।

सौभाग्य से, यदि आप विशिष्ट का पालन करते हैं तो डेरिवेटिव्स को ढूंढना एक व्यवस्थित प्रक्रिया है (जरूरी नहीं कि आसान) हो विभेदन नियम ।सबसे अधिक इस्तेमाल किए जाने वाले नियम हैं पmurauguth नियम , तंग और तिहाई ।

रैखिक या तमाम वैचारिक रूप से एक फ़ंक्शन को कम से कम स्थानीय स्तर पर एक फ़ंक्शन को अनुमानित करने का प्रयास करें, और आपको एक फ़ंक्शन के व्यवहार के बारे में बहुत कुछ बता सकते हैं, एक निश्चित बिंदु के करीब।