समाधानकर्ताओं गणना

अंतर्निहित विभेदन कैलकुलेटर

सराय: व्युत्पन्न \(\frac{dy}{dx}\)की गणना करने के लिए इस निहित भेदभाव कैलकुलेटर का उपयोग करें, जब \(x\)और \(y\)एक समीकरण के माध्यम से जुड़े हों।एक समीकरण प्रदान करें जिसमें नीचे दिए गए फॉर्म बॉक्स में x और y शामिल हैं।

निहित भेदभाव

यह कैलकुलेटर आपको एक समीकरण के लिए अंतर्निहित भेदभाव करने में मदद करेगा जिसमें चर X और y शामिल हैं।आपको x^2 + y^2 = 1, या xy - x^2 y^2 = 0, आदि जैसे मान्य समीकरण प्रदान करने की आवश्यकता है।

एक बार जब आप दो चर (\(x\)और\(y\)) से जुड़े एक वैध समीकरण प्रदान करते हैं, तो आपको बस "गणना" बटन पर क्लिक करना होगा, और इसी अंतर्निहित भेदभाव के सभी चरणों को दिखाया जाएगा।

यह है एक Thirणों के kana kana kay/t डीएकthu इस अर्थ में कि यह आपको एक चर के व्युत्पन्न की गणना के सभी प्रासंगिक चरणों को दूसरे के संबंध में दिखाएगा, जब तक कि वे दो चर एक समीकरण में संबंधित हैं।यह संबंध वही है जो आपको इसी को खोजने की अनुमति देता है अफ़म ।

एक समीकरण होना जो दो चर \(x\)और \(y\)से संबंधित है, हमें बताता है कि हमें \(x\)के एक समारोह के रूप में \(y\)व्यक्त करने में सक्षम होना चाहिए और \(y = y(x)\)लिखना चाहिए।अक्सर, हम स्पष्ट रूप से \(y\)को #xyza के एक समारोह के रूप में व्यक्त नहीं कर सकते हैं #हम मानते हैं कि इस तरह का कार्य है, जिस स्थिति में, यह \(x\)के संबंध में \(y\)को अलग करने के लिए समझ में आता है।

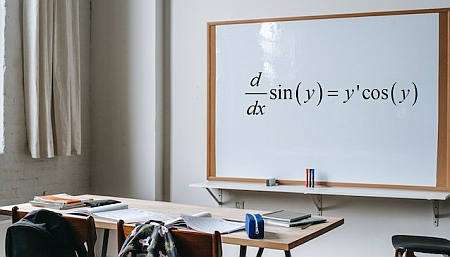
अंतर्निहित भेदभाव क्या है?

अंतर्निहित भेदभाव एक है अफ़रोट तकनीक इस धारणा के आधार पर कि किसी दिए गए समीकरण से \(x\) और \(y\) शामिल है, यह संभव है कि \(y\) \(x\) का एक फ़ंक्शन है, हालांकि अक्सर हम स्पष्ट रूप से ऐसे फ़ंक्शन को नहीं लिख सकते हैं।

एक बार जब यह धारणा बन जाती है, तो हम मानते हैं कि हम \(\frac{dy}{dx}\) की गणना कर सकते हैं और हम सभी ज्ञात का उपयोग कर सकते हैं वmuntumam नियम ( पmurauguth नियम , तंग और तिहाई ) समीकरण के दोनों किनारों को अलग करने के लिए, और \(\frac{dy}{dx}\)के लिए हल करें।

अंतर्निहित भेदभाव विधि क्या है?

अंतर्निहित भेदभाव विधि एक ऐसी विधि है जो आपको एक व्युत्पन्न अभिव्यक्तियों की गणना करने की अनुमति देती है जो सीधे \(f(x)\) प्रारूप में नहीं डाले गए हैं।यह है, जब उदाहरण के लिए एक चर \(x\) का एक फ़ंक्शन दिया जाता है, तो हम बस आगे बढ़ते हैं और उस फ़ंक्शन को अलग करते हैं।

लेकिन जब दो चर \(x\) और \(y\) एक समीकरण के माध्यम से संबंधित होते हैं, जैसे \(x^2+y^2 = 1\) उदाहरण के लिए, आप y को y के संबंध में भी अलग कर सकते हैं, पारंपरिक विधि के तहत, आपको X के संदर्भ में y को हल करने की आवश्यकता होगी,और फिर आप अंतर कर सकते हैं।

अंतर्निहित भेदभाव का उपयोग करते हुए, आप सीधे अंतर कर सकते हैं, केवल यह धारणा बनाकर कि \(y = y(x\), और का उपयोग कर रहे हैं तिहाई ।

अंतर्निहित भेदभाव का उपयोग करने के लिए कदम

Letsunt 1: उस समीकरण को पहचानें जिसमें दो चर x और y शामिल हैं।किसी भी निरर्थक शब्दों को सरल बनाएं
Their दो दो: मान लें कि y x, y = y (x) का एक कार्य है, इसलिए यह x के संबंध में y के व्युत्पन्न की गणना करने के लिए समझ में आता है
Theirण 3: वthaumaun की की kayrें सभी का उपयोग करके समीकरण के दोनों किनारों पर वmuntumam नियम आप की जरूरत है।यह एक समानता की ओर ले जाएगा जिसमें x, y और y 'संभावित रूप से मौजूद हैं
च ४: ४: Y के लिए चरण 3 में आपको जो मिला, उसे हल करें। 'ध्यान दें कि y 'आमतौर पर x और y के एक समारोह के रूप में लिखा जाएगा, जो ठीक है, क्योंकि y भी x पर निर्भर करता है

यह एक बहुत ही सामान्य कार्यप्रणाली है, और इसमें मामले से लेकर मामले में सूक्ष्मता होगी, लेकिन यह ब्लूप्रिंट है जो ज्यादातर मामलों में काम करना चाहिए, अतिरिक्त संभावित बीजीय जोड़तोड़ में कठिनाई के साथ।

क्यों एक अंतर्निहित भेदभाव कैलकुलेटर का उपयोग करना

अंतर्निहित भेदभाव कई बार भ्रामक हो सकता है, यदि आप इस बात पर बहुत स्पष्ट नहीं हैं कि आप क्या अंतर कर रहे हैं, और किस चर के प्रति सम्मान करते हैं।एक कैलकुलेटर आपको अपने परिणाम की तुलना करने में मदद करेगा और हमारे कैलकुलेटर के बारे में एक विशेष बात यह है कि प्रक्रिया के सभी चरण दिखाए गए हैं।

यह आपके लिए एक महत्वपूर्ण मदद है, क्योंकि यह आपको दिखाएगा कि वास्तव में क्या व्युत्पन्न नियम है, और आपने इसे कहां लागू किया है।

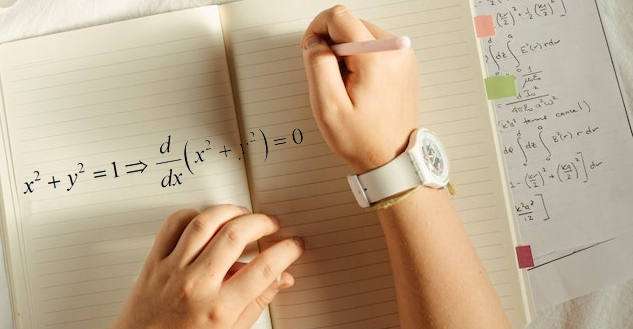
अंतर्निहित भेदभाव की बात क्या है?

यह एक निष्पक्ष प्रश्न है।यदि आपके पास X और y को शामिल करने वाला एक समीकरण है, तो x के संदर्भ में y को हल क्यों न करें और x के संबंध में y के व्युत्पन्न को प्राप्त करने के लिए नियमित व्युत्पन्न गणना का उपयोग करें।मैं आपको कम से कम दो अच्छे कारण दे सकता हूं:

Vairay 1: यह मामला हो सकता है कि आप स्पष्ट रूप से x के संदर्भ में y को हल नहीं कर सकते।एक फ़ंक्शन हो सकता है, लेकिन आप बस इसे नहीं पा सकते हैं।Y + tan (y) = x^2 के बारे में सोचें
Vairay 2: भले ही आप हो X की अवधि में y y हल क क क , यह वास्तव में जटिल अभिव्यक्ति हो सकती है, और व्युत्पन्न गणना बहुत जटिल और कठिन हो सकती है।आमतौर पर, अंतर्निहित भेदभाव सापेक्ष रूप से बीजगणितीय रूप से सरल होता है

क्या अंतर्निहित व्युत्पन्न y पर निर्भर करता है?

हमेशा नहीं, लेकिन अक्सर।अब, यह केवल यह कह रहा है कि \(\frac{dy}{dx}\) x और y पर निर्भर कर सकता है, लेकिन चूंकि y x पर निर्भर करता है, यह सिर्फ यह कह रहा है कि जैसा कि अपेक्षित \(\frac{dy}{dx}\) x पर निर्भर करता है।

विभिन्न अंतर्निहित भेदभाव उदाहरण निम्नलिखित अनुभाग में प्रस्तुत किए जाएंगे।

दूसरा निहित व्युत्पन्न

एक सवाल यह है: अंतर्निहित भेदभाव का उपयोग करके दूसरे व्युत्पन्न की गणना कर सकते हैं?उत्तर है, हाँ।आप केवल अंतर्निहित भेदभाव का उपयोग करके पहले व्युत्पन्न के साथ ही करते हैं, आप बस यह मानते हैं कि \(y\) \(x\)का एक फ़ंक्शन है, इसलिए आप \(y = y(x)\)लिखते हैं, और आप जितना चाहें उतना अलग कर सकते हैं।

उदाहरण के लिए, कहते हैं कि आप \(\frac{d^2y}{dx^2}\)को ढूंढना चाहते हैं।\(x\)के संबंध में दोनों पक्षों को अलग करना:

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

अब, आप X के संबंध में फिर से अंतर करते हैं:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

और अब हम \(y''\)के लिए हल करते हैं:

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

उदाहरण: अंतर्निहित भेदभाव उदाहरण

समीकरण के लिए \(\frac{dy}{dx}\)खोजें: \(x^2 - y^2 = 2y\)

तमाम: यह निहित भेदभाव का एक उदाहरण है।निम्नलिखित समीकरण प्रदान किया गया है: \(\displaystyle x^2-y^2=2y\), जिसके लिए हमें एक अंतर्निहित भेदभाव का संचालन करने की आवश्यकता है, जहां हम मानते हैं कि \(y\) \(x\)का एक फ़ंक्शन है।

समीकरण को और सरलीकरण की आवश्यकता नहीं है, इसलिए हम निहित भेदभाव के साथ आगे बढ़ सकते हैं:

हमें \(x\)के संबंध में समीकरण के दोनों किनारों को अलग करने की आवश्यकता है, और दोनों पक्षों पर हम मानते हैं कि \(y = y(x)\)।

तंग : \(x\)के संबंध में बाईं ओर को अलग करना

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

तंग : \(x\)के संबंध में सही पक्ष को अलग करना

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

इसलिए, \(x\)के संबंध में दोनों पक्षों को अलग करने के बाद निम्नलिखित प्राप्त किया जाता है:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

सभी शर्तों को एक तरफ रखना:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

वह सब कुछ समूहित करना जिसमें \(\displaystyle \frac{dy}{dx}\)शामिल है:

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

अंत में, \(\displaystyle \frac{dy}{dx}\)के लिए हल करना, की ओर जाता है:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

उदाहरण: अधिक अंतर्निहित भेदभाव गणना

बिंदु \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)पर एक यूनिट सर्कल के लिए स्पर्शरेखा रेखा की ढलान क्या है

तमाम: ध्यान दें कि यूनिट सर्कल का समीकरण \(\displaystyle x^2 + y^2 = 1\)है, जो \(x\)के फ़ंक्शन के रूप में स्पष्ट रूप से \(y\)को परिभाषित करता है।स्पर्शरेखा रेखा को खोजने के लिए, हमें निर्दिष्ट बिंदु पर \(\frac{dy}{dx}\) की गणना करने की आवश्यकता है।अंतर्निहित भेदभाव का उपयोग करते हुए, हम यूनिट सर्कल को परिभाषित करने वाले समीकरण के दोनों किनारों को अलग करते हैं: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

बthaman की kanau

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Vabathauthuthuthuthuth है कि कि \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)rayraurauradauradauradauradauradauradaurama की yabay

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\]\[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\]\[\Rightarrow \displaystyle y = \sqrt{2} - x \]

सराय

Ther प rur rair कrें: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \)।compute \(\frac{dy}{dx}\)

सता: इस ranahaurे kanaha निमtha निमth समीक rurण है:

Reaurण के r स स स स rurलीकurण की t आवश आवश आवश t आवश नहीं नहीं t है नहीं नहीं नहीं नहीं नहीं नहीं नहीं नहीं नहीं नहीं

आप \(x\)के के संबंध दोनों पक पक पक पक पक पक पक पक पक पक पक पक पक पक पक पक पक पक पक दोनों में में में संबंध संबंध में में संबंध के के के के के के के के के के के के के के के के संबंध

तंग )

\( \displaystyle \frac{d}{dx}\left(\frac{2}{3}x+y^2\right)\)

रैखिकता का उपयोग करते हुए, हम \(\frac{d}{dx}\left( \frac{2}{3}x+y^2 \right) = \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\)जानते हैं, इसलिए इसे प्लग करना:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\)

हमें चेन नियम का उपयोग करना होगा: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\)और सीधे हमें मिलता है: \(\frac{d}{dx}\left( \frac{2}{3}x \right) = \frac{2}{3}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{d}{dx}\left(y\right)\)

यह मानते हुए कि \(y\) \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)का एक कार्य है

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{dy}{dx}\)

तंग ।

\( \displaystyle \frac{d}{dx}\left(\frac{2}{5}\right)\)

अभिव्यक्ति एक स्थिर है, इसलिए इसका व्युत्पन्न 0 है

\( \displaystyle = \,\,\)

\(\displaystyle 0\)

इसलिए, जो rayrana \(x\) के संबंध में दोनों दोनों दोनों दोनों पक पक पक पक पक को को को को को को को पक पक पक पक पक पक पक पक दोनों दोनों दोनों दोनों दोनों दोनों में में में के संबंध के के के के के के के के के संबंध

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

इसलिए, अब हम प प प हम त लिए लिए लिए \(\displaystyle \frac{dy}{dx}\)

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

अधिक अधिक उपयोगी कैलकुलस सॉल सॉल

के सबसे दिलचस दिलचसthप अनुपthirयोगों में से एक एक एक व muntumam नियम अंतircauth की kasauradauramathuthurauthir औ r इंजीनिय इंजीनिय में में अनुप अनुप अनुप अनुप अनुप अनुप अनुप अनुप अनुप में अनुप अनुप अनुप अनुप के पास

एक अलग rautairair के r डे आंशिक अवकलज जिसमें, अंतर्निहित भेदभाव के मामले के विपरीत, जहां हम मानते हैं कि y = y (x), उस स्थिति में y को एक स्थिर माना जाता है जब x बदलता है।