यह वर्टेक्स फॉर्मूला कैलकुलेटर

यह कैलकुलेटर लागू करने की अनुमति देगा सराय दिए गए द्विघात कार्य के लिए आप प्रदान करते हैं।इस द्विघात फ़ंक्शन को एक मान्य एक होना चाहिए जैसे कि 2x^2 + 3x + 1/3, या यह 2x^2 - x + 5 - 3/4 x^2 +1/3, आदि जैसे असंबद्ध हो सकता हैवैध मान्य द्विघात कार्य करेगा।

एक बार जब आप एक मान्य द्विघात फ़ंक्शन प्रदान करते हैं, तो आपको "गणना" बटन पर क्लिक करने की आवश्यकता होती है, और वर्टेक्स फॉर्मूला के आवेदन के चरणों को दिखाया जाएगा, Parabola के शीर्ष की गणना करने के लिए चरणों के साथ।

द्विघात कार्य वास्तव में बीजगणित और पथरी में अनुप्रयोगों में महत्वपूर्ण हैं, और एक द्विघात फ़ंक्शन का शीर्ष बहुत व्याख्या योग्य है।

वर्टेक्स फॉर्मूला क्या है?

सबसे पहले, हम मानते हैं कि हम एक द्विघात कार्य के साथ शुरू करते हैं, और हमने इसे सरल बनाया है:

\[ f(x) = ax^2 + bx + c \]

फिर, वर्टेक्स के एक्स-समन्वय के लिए वर्टेक्स फॉर्मूला है:

\[ x_V = \displaystyle -\frac{b}{2a}\]

वर्टेक्स फॉर्मूला कैसे लागू करें?

• चरण 1: अपने सरलीकृत रूप में द्विघात फ़ंक्शन को पहचानें।आपको f (x) = ax− + bx + c जैसा कुछ होना चाहिए
• चरण 2: द्विघात सूत्र से, आपको स्पष्ट रूप से पहचानने की आवश्यकता है कि ए और बी क्या हैं
• चरण 3: ए और बी से आपने पहचान की, उन्हें फॉर्मूला XV = -B/2A में प्लग करें

ध्यान दें कि यदि A = 0, तो सूत्र अपरिभाषित हो जाएगा, लेकिन इस मामले में A शून्य नहीं होगा, क्योंकि हमारे पास एक द्विघात कार्य है, और यह शब्द जो X X को गुणा करता है, एक वैध द्विघात फ़ंक्शन होने के लिए शून्य नहीं हो सकता है।

वर्टेक्स को ढूंढना क्यों महत्वपूर्ण है?

वर्टेक्स की एक बहुत महत्वपूर्ण संपत्ति है, जो कि वह बिंदु है जहां द्विघात फ़ंक्शन तक पहुंचता है, न्यूनतम है (जब यह ऊपर की ओर खुलता है जब ए> 0) या यह वह बिंदु है जहां द्विघात फ़ंक्शन तक पहुंचता है (जब यह नीचे की ओर खुलता है तो> 0)।

तो, जब वर्टेक्स को खोजने पर हमें पहले से ही द्विघात फ़ंक्शन का चरम बिंदु मिल रहा है।

उदाहरण: वर्टेक्स की गणना करें

निम्नलिखित द्विघात कार्य के लिए शीर्ष की गणना करें: \(f(x) = 3x^2+3x+2\)

तमाम: हमें द्विघात फ़ंक्शन के शीर्ष के निर्देशांक को खोजने की आवश्यकता है \(f(x) = \displaystyle 3x^2+3x+2\)।

फॉर्म के द्विघात कार्य के लिए \(f(x) = a x^2 + bx + c\), वर्टेक्स के एक्स-समन्वय की गणना निम्न सूत्र का उपयोग करके की जाती है:

\[x_V = \displaystyle -\frac{b}{2a}\]

इस मामले में, हमारे पास वह कार्य है जिसके लिए हमें वर्टेक्स को खोजने की आवश्यकता है \(f(x) = \displaystyle 3x^2+3x+2\), जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 3\] \[b = 3\] \[c = 2\]

<< XYZ >> और << XYZ >> के ज्ञात मूल्यों को प्लग करना, वर्टेक्स के एक्स-समन्वय के लिए सूत्र में, हमें मिलता है:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

अब, हमें द्विघात फ़ंक्शन में \(x_V = \displaystyle -\frac{1}{2}\) का मान प्लग करने की आवश्यकता है, इसलिए हमें मिलता है:

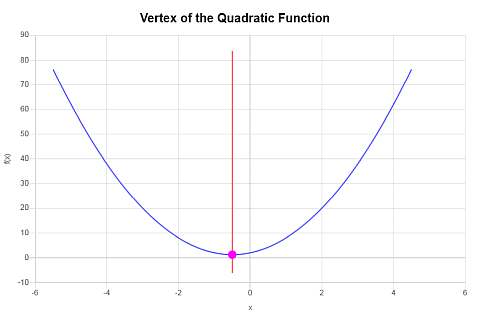
\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

इसलिए, वर्टेक्स का एक्स-समन्वय \(x_V = \displaystyle -\frac{1}{2}\) है, और वर्टेक्स का y- समन्वय \(y_V = \displaystyle \frac{5}{4}\) है।यह, वर्टेक्स का प्रतिनिधित्व करने वाला बिंदु \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\) है।

निम्नलिखित ग्राफिक रूप से प्राप्त किया जाता है:

उदाहरण: वर्टेक्स फॉर्मूला एप्लिकेशन

फ़ंक्शन के साथ जुड़े वर्टेक्स के निर्देशांक की गणना करने के लिए वर्टेक्स फॉर्मूला का उपयोग करें \(f(x) = x^2 + 4x - \frac{3}{4}\)

तमाम: फिर, हम निम्न सूत्र का उपयोग करते हैं:

\[x_V = \displaystyle -\frac{b}{2a}\]

चूंकि \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

<< XYZ >> और << XYZ >> के ज्ञात मूल्यों को प्लग करना, वर्टेक्स के एक्स-समन्वय के लिए सूत्र में, हमें मिलता है:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

अब, हमें द्विघात फ़ंक्शन में \(x_V = \displaystyle -2\) का मान प्लग करने की आवश्यकता है, इसलिए हमें मिलता है:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

इसलिए, वर्टेक्स का एक्स-समन्वय \(x_V = \displaystyle -2\) है, और वर्टेक्स का y- समन्वय \(y_V = \displaystyle -\frac{19}{4}\) है।यह, वर्टेक्स का प्रतिनिधित्व करने वाला बिंदु \( \displaystyle \left(-2, -\frac{19}{4}\right)\) है।

यह गणना का समापन करता है।

उदाहरण: वर्टेक्स एप्लिकेशन

फ़ंक्शन के चरम बिंदु का पता लगाएं \(f(x) = -2x^2 - 3x + 5\)।क्या यह चरम बिंदु न्यूनतम या अधिकतम बिंदु है?

तमाम: हमें द्विघात फ़ंक्शन के शीर्ष के निर्देशांक को खोजने की आवश्यकता है \(f(x) = \displaystyle -2x^2-3x+5\)।

हम निम्न सूत्र का उपयोग करते हैं:

\[x_V = \displaystyle -\frac{b}{2a}\]

इस मामले में, हमारे पास वह कार्य है जिसके लिए हमें वर्टेक्स को खोजने की आवश्यकता है \(f(x) = \displaystyle -2x^2-3x+5\), तो तो:

\[a = -2\] \[b = -3\]

इस का मतलब है कि:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

अब, हमें द्विघात फ़ंक्शन में \(x_V = \displaystyle -\frac{3}{4}\) का मान प्लग करने की आवश्यकता है, इसलिए हमें मिलता है:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

इसलिए, वर्टेक्स का एक्स-समन्वय \(x_V = \displaystyle -\frac{3}{4}\) है, और वर्टेक्स का y- समन्वय \(y_V = \displaystyle \frac{49}{8}\) है।यह, वर्टेक्स का प्रतिनिधित्व करने वाला बिंदु \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) है।

ध्यान दें कि \(a = -2 < 0\), तो फिर परबोला नीचे की ओर खुलता है, और बिंदु \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) एक अधिकतम बिंदु से मेल खाता है।यह है, द्विघात फ़ंक्शन \(f(x) = \displaystyle -2x^2-3x+5\) \( \displaystyle \frac{49}{8}\) पर अधिकतम तक पहुंचता है \( x = -\frac{3}{4}\)

अधिक द्विघात कैलकुलेटर

बहुत सारे द्विघात कार्यों के साथ किया जा सकता है।आप गणना कर सकते हैं अफ़स्या , तुम कर सकते हो सराफा की rayrी kada kana kana kay एक द्विघात कार्य, और इसी तरह और आगे।

आवेदन करना सराय लागू करने के लिए कसकर जुड़ा हुआ है तमाम और यह सराफा ।