तर्कसंगत कार्य

यह तर्कसंगत फ़ंक्शन कैलकुलेटर आपको दिखाए गए सभी चरणों के साथ, आपके द्वारा प्रदान किए गए तर्कसंगत फ़ंक्शन के सबसे प्रासंगिक बिंदुओं का विश्लेषण करने की अनुमति देगा। आमतौर पर, अधिकांश तर्कसंगत कार्यों के लिए आप अंतःखंड, लंबवत अनंतस्पर्शी और उसका ग्राफ़ पा सकते हैं। कुछ विशिष्ट तर्कसंगत कार्यों में क्षैतिज अनंतस्पर्शी भी होंगे।

आप जिस प्रकार का फ़ंक्शन प्रदान कर सकते हैं वह 'f(x)=1/x - x' जैसा है, या उच्च डिग्री के बहुपदों से युक्त कुछ है जैसे 'f(x) = (x^3-1)/(x^2+x )'

एक बार वैध तर्कसंगत फ़ंक्शन प्रदान किए जाने के बाद, आप गणना बटन पर क्लिक कर सकते हैं, और आपको आपके लिए दिखाए गए सभी चरण मिल जाएंगे।

एक तर्कसंगत फ़ंक्शन की मुख्य विशेषताओं में से एक यह है कि आप गणना को अधिकतर समस्या तक कम कर सकते हैं बहुपद समीकरणों को हल करना , जो कि "सरलतम" प्रकारों में से एक है समीकरण जिन्हें आप हल कर सकते हैं .

एक तर्कसंगत कार्य क्या है

एक तर्कसंगत कार्य एक ऐसा कार्य है जिसमें शामिल होता है दो बहुपदों का भागफल \(P(x)\) और \(Q(x)\), जहां भाजक \(Q(x)\) शून्य बहुपद के बराबर नहीं है। तो फिर, तर्कसंगत कार्य सूत्र है

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

उदाहरण के लिए, फ़ंक्शन

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

एक तर्कसंगत फलन है, क्योंकि यह बिल्कुल दो बहुपदों का भागफल है। लेकिन उदाहरण के लिए

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

तर्कसंगत नहीं है क्योंकि भाजक एक बहुपद नहीं है। ध्यान दें कि जब हम कहते हैं कि भाजक \(Q(x)\) शून्य बहुपद के बराबर नहीं है, तो हम यह नहीं कह रहे हैं कि \(Q(x)\) में शून्य नहीं हो सकते। उदाहरण के लिए, \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \) के इस मामले में, भाजक \(Q(x) = x + 1\) है, जिसमें \(x = -1\) पर एक शून्य है।

हम जो नहीं चाहते वह कुछ ऐसा है

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

क्योंकि यद्यपि इस मामले में \(Q(x) = 0\) तकनीकी रूप से एक बहुपद है, यह शून्य बहुपद है (जो हर जगह शून्य है)।

एक परिमेय फलन की गणना के लिए चरण

• स्टेप 1: सबसे पहले, सुनिश्चित करें कि आपके पास एक परिमेय फलन है, जिसके लिए आप अंश P(x) और हर Q(x) की पहचान कर सकते हैं
• चरण दो: यदि आपको ऊपर वर्णित संरचना पूरी तरह से नहीं मिलती है, तो आप रुक जाएं। आपको शब्दों को एक साथ समूहित करने की आवश्यकता हो सकती है बीजगणितीय कटौती .
• चरण 3: आपको P(x) और Q(x), यदि कोई हो, के वास्तविक शून्य खोजने की आवश्यकता है। पाए गए निष्कर्ष P(x) और Q(x) दोनों के शून्यों से कसकर संबंधित होंगे।
• चरण 4: Y-इंटरसेप्ट को खोजने के लिए, आप f(0) की गणना करके फ़ंक्शन का शून्य पर मूल्यांकन करते हैं। यदि x = 0, Q(x) का शून्य नहीं है तो y-अवरोधन अच्छी तरह से परिभाषित किया जाएगा
• चरण 5: एक्स-इंटरसेप्ट्स को खोजने के लिए, आपको P(x) के शून्य मिलते हैं जो Q(x) के शून्य नहीं हैं
• चरण 6: ऊर्ध्वाधर अनंतस्पर्शी खोजने के लिए, आपको Q(x) के शून्य खोजने होंगे जो P(x) के शून्य नहीं हैं
• चरण 7: क्षैतिज अनंतस्पर्शी खोजने के लिए, आपके पास यह होना चाहिए कि Q(x) की डिग्री घात P(x) से अधिक या उसके बराबर हो

ध्यान दें कि जैसा कि अपेक्षित था, एक तर्कसंगत कार्य का विश्लेषण किस पर निर्भर करता है एक बहुपद के शून्य खोजना , और फिर सभी निष्कर्षों को एक साथ रखना। .

ध्यान दें कि एक परिमेय फलन का प्रांत भाजक Q(x) के शून्य को छोड़कर संपूर्ण वास्तविक रेखा है। यदि Q(x) का शून्य है जो कि P(x) का भी शून्य है, तो असंततता की मरम्मत की जा सकती है। एक परिमेय फलन की सीमा P(x) और Q(x) की डिग्री पर निर्भर करेगी।

तर्कसंगत कार्यों का उपयोग क्यों करें?

तर्कसंगत कार्यों का उपयोग किया जाता है क्योंकि वे बहुपदों के प्राकृतिक विस्तार हैं। कोई इन्हें किसी फ़ंक्शन की जटिलता के अगले चरण के रूप में देख सकता है। जैसा कि हम जानते हैं, बहुपद अभिव्यक्तियाँ ये सबसे सरल फ़ंक्शन हैं जिन्हें हम पा सकते हैं, लेकिन फिर भी ये सबसे उपयोगी भी हैं।

तर्कसंगत समीकरण आमतौर पर अधिक उन्नत मिश्रण समस्याओं में दिखाई देंगे, और फिर भी, उन्हें संभालना आश्चर्यजनक रूप से सरल है, बशर्ते कि इसमें शामिल बहुपद पर्याप्त सरल हों। हम जानते हैं द्विघात समीकरणों को कैसे हल करें , लेकिन घात 3 और उससे अधिक के बहुपदों के लिए चीजें अधिक रोएंदार हो सकती हैं।

क्या बहुपद फलन भी तर्कसंगत फलन हैं?

हाँ, यदि P(x) एक बहुपद है, तो P(x) भी परिमेय है, क्योंकि हम लिख सकते हैं:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

और Q(x) = 1 एक वास्तविक बहुपद है। दूसरा तरीका सत्य नहीं है: एक परिमेय फलन आवश्यक रूप से एक बहुपद नहीं होता है। ऐसा क्यों? क्योंकि स्वाभाविक रूप से, जब तक Q(x) = 1 नहीं होता, जब भी आपके पास \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \) होता है, तो आपके पास यह नहीं होगा कि बहुपद की परिभाषा के अनुसार सभी पद मुक्त पद होंगे।

अधिक औपचारिक रूप से, उपयोग करना शेष प्रमेय , हमारे पास है

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

जहां \(d(x)\) एक बहुपद है, लेकिन \frac{r(x)}{Q(x)} नहीं है, क्योंकि r(x) की घात Q(x) की घात से कम है।

उदाहरण: तर्कसंगत कार्यों के साथ कार्य करना

: \(f(x) = \frac{x^2-1}{x+1}\) के अंतःखंड और अनंतस्पर्शी और ग्राफ़ खोजें

समाधान:

हमें निम्नलिखित फ़ंक्शन प्रदान किया गया है:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

हमें अंतःखंड और स्पर्शोन्मुख, यदि कोई हो, खोजने की आवश्यकता है। उसके बाद, फ़ंक्शन का ग्राफ़ प्रस्तुत किया जाएगा।

आइए दिए गए फ़ंक्शन के शून्य ज्ञात करें। हमें निम्नलिखित तर्कसंगत समीकरण को हल करने की आवश्यकता है:

\[\frac{x^2-1}{x+1}=0\]

ध्यान दें कि \(x \ne -1\) के लिए हम इसे इस प्रकार सरल बना सकते हैं:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

सहायक अंश समीकरण

अब हम अंश को शून्य के बराबर सेट करते हैं और समाधान ढूंढते हैं। फिर, वे मूल जो हर को शून्य के बराबर नहीं बनाते, तर्कसंगत समीकरण के समाधान होंगे।

अंश के मूल ज्ञात करने के लिए निम्नलिखित को हल करने की आवश्यकता है: \(x^2-1=0\)

फार्म \(a x^2 + bx + c = 0\)के एक द्विघात समीकरण के लिए, जड़ों को निम्न सूत्र का उपयोग करके गणना की जाती है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस मामले में, हमारे पास है कि हमें जिस समीकरण को हल करने की आवश्यकता है वह \(\displaystyle x^2-1 = 0\)है, जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 1\] \[b = 0\] \[c = -1\]

सबसे पहले, हम जड़ों की प्रकृति का आकलन करने के लिए भेदभाव की गणना करेंगे।भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

चूंकि इस मामले में हमें भेदभावपूर्ण \(\Delta = \displaystyle 4 > 0\)है, जो सकारात्मक है, हम जानते हैं कि समीकरण में दो अलग -अलग वास्तविक जड़ें हैं।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

सहायक हर समीकरण

हमें हर के मूल ज्ञात करने होंगे: \(x+1=0\)

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने पर \(x=-1\) प्राप्त होता है।

अंश और हर शून्य

ऊपर दिखाए गए विश्लेषण के आधार पर, दिए गए परिमेय फलन के अंश के वास्तविक शून्य \( x_{ 1} = -1\) और \( x_{ 2} = 1\) हैं।

यह भी पाया गया कि हर में एक वास्तविक शून्य है, जो \( x_{ 1} = -1\) है।

एक्स-इंटरसेप्ट्स ढूँढना

अंश के शून्यों के आधार पर जो हर के शून्य नहीं हैं, हम पाते हैं कि एक x-अवरोधन है, जो \(\left(1, 0\right)\) है।

वाई-इंटरसेप्ट ढूँढना

\(x = 0\) पर दिए गए फ़ंक्शन का मूल्यांकन करके, हम पाते हैं कि:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

तो फिर y-अवरोधन \( \left(0, -1\right)\) है।

लंबवत अनंतस्पर्शी

शून्यों का विश्लेषण करने के बाद, यह निष्कर्ष निकाला गया कि फ़ंक्शन में लंबवत अनंतस्पर्शी नहीं हैं।

क्षैतिज asymptotes

ध्यान दें कि अंश की डिग्री \(2\) है और हर की डिग्री \(1\) है, और फिर, चूंकि अंश में बहुपद की डिग्री हर में से एक से अधिक है, हम निष्कर्ष निकालते हैं कि कोई क्षैतिज नहीं है स्पर्शोन्मुख.

निम्नलिखित ग्राफ प्राप्त होता है:

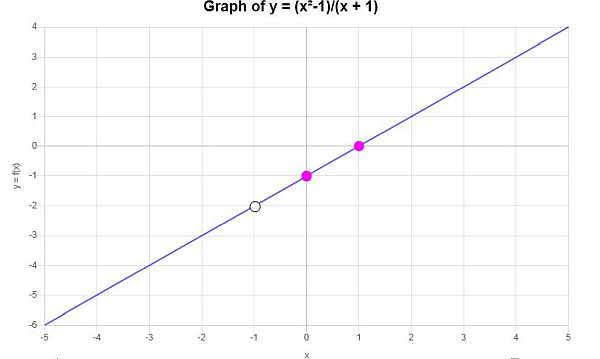
उदाहरण: क्षैतिज अनंतस्पर्शी

क्या इस तर्कसंगत फ़ंक्शन में क्षैतिज अनंतस्पर्शी है: \(f(x) = \frac{x^2-1}{x^2+1}\)?

समाधान: स्पष्ट रूप से इस मामले में, फ़ंक्शन में दो बहुपदों का भागफल होता है, और उन दोनों की डिग्री 2 के बराबर होती है। इसका मतलब है, उनकी डिग्री समान है और इसलिए, एक क्षैतिज अनंतस्पर्शी है।

हम इसे सीमाओं का उपयोग करके भी देख सकते हैं:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

जिसका अर्थ है कि क्षैतिज अनंतस्पर्शी \(y = 1\) है। इससे गणना समाप्त होती है.

उपयोगी फ़ंक्शन कैलकुलेटर

फ़ंक्शंस मौलिक गणितीय वस्तुएं हैं, जो विभिन्न चर के बीच संबंधों को समाहित करती हैं। इसका उपयोग करना समारोह कैलकुलेटर यह आपको उन कार्यों को व्यवस्थित रूप से निपटाने में मदद कर सकता है जिन्हें हाथ से संभालना बहुत जटिल हो सकता है।

तर्कसंगत कार्यों का रेखांकन सबसे आम खिलौना उदाहरणों में से एक है जो छात्र बीजगणित और कैलकुलस में सीखते हैं, और हालांकि शायद तर्कसंगत कार्य अनुप्रयोगों में अक्सर दिखाई नहीं देते हैं, इससे निपटने के लिए आवश्यक विश्लेषणात्मक कौशल अमूल्य साबित हो सकते हैं

उसके लिए भी यही तर्कसंगत समीकरणों को हल करना , जहां बीजगणितीय अभिव्यक्तियों में हेरफेर करने और उन्हें उनकी निचली शर्तों तक कम करने के सिद्धांत अधिक उन्नत कौशल की उपलब्धि के लिए बेहद शक्तिशाली होंगे।

अब, यदि हम फ़ंक्शन के बारे में बात कर रहे हैं, तो हम इसे नहीं भूल सकते किसी फ़ंक्शन के व्युत्पन्न की गणना , एकीकरण और अन्य अधिक उन्नत इनफिनिटसिमल तकनीकें।