समाधानकर्ताओं गणना

ट्रिग डेरिवेटिव

सराय: आपके द्वारा प्रदान किए गए किसी भी फ़ंक्शन के व्युत्पन्न की गणना करने के लिए TRIG व्युत्पन्न कैलकुलेटर का उपयोग करें जिसमें त्रिकोणमितीय कार्यों को शामिल किया गया है, जो सभी चरणों को दर्शाता है।कृपया उस फ़ंक्शन को टाइप करें जिसे आप नीचे दिए गए फॉर्म बॉक्स में अंतर करना चाहते हैं।

ट्रिग डेरिवेटिव के बारे में अधिक

त्रिकोणमितीय डेरिवेटिव खोजने के लिए इस कैलकुलेटर का उपयोग करें, जो इस मामले में हम किसी भी मान्य विभेदक फ़ंक्शन को मानते हैं जिसमें एक या अधिक प्राथमिक ट्रिग फ़ंक्शन शामिल है।

इस कैलकुलेटर के लिए एक मान्य फ़ंक्शन का एक उदाहरण f (x) = sin (x)/x, या f (x) = x*sin (x^3) है, बस एक उदाहरण दिया गया है।

फिर, जब आप पहले से ही संबंधित फ़ंक्शन टाइप कर चुके हैं, तो आप फिर "गणना" बटन पर क्लिक कर सकते हैं, इसलिए आपको दिखाए गए व्युत्पन्न की गणना के सभी चरणों को प्राप्त करने के लिए।

त्रिकोणमितीय कार्य पथरी में एक महत्वपूर्ण भूमिका निभाते हैं, साथ ही साथ Rairिवेटिव की kayna सामान्य रूप में।अंततः, अधिक जटिल कार्य सरल ट्रिग कार्यों के लिए व्युत्पन्न की गणना के लिए उनके डेरिवेटिव को कम कर सकते हैं।

बुनियादी ट्रिग व्युत्पन्न

व्युत्पन्न नियमों का उपयोग करने का विचार एक जटिल फ़ंक्शन को तोड़ना और ज्ञात कार्यों के डेरिवेटिव का उपयोग करके इसे अलग करना है।विशेष रूप से, साइन, कोसाइन, स्पर्शरेखा और कोटैंगेंट जैसे सरल ट्रिग फ़ंक्शंस उस में एक महत्वपूर्ण भूमिका निभाएंगे।

मूल ट्रिग डेरिवेटिव क्या हैं?

ट refir व \(\frac{d}{dx} \sin (x) = \cos(x)\)
टrifur व \(\frac{d}{dx} \cos (x) = -\sin(x)\)
टrifur व \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
ट reprifuntumautumautimaum \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
टrifur व \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
टrifur व \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

ये मूल डेरिवेटिव हैं जिन्हें आपको बहुत जानना होगा, और संभवतः उपयोग करने के लिए याद रखें वmuntumam नियम अधिक जटिल डेरिवेटिव की गणना करने के लिए

डिग्री में ट्रिग डेरिवेटिव हैं?

नहीं, ट्रिग फ़ंक्शंस के व्युत्पन्न में हैं रोटी , इसलिए ट्रिग डेरिवेटिव्स ने इस तथ्य को दर्शाया कि तर्क एक्स को रेडियन में मापा जाता है।

इसलिए, उदाहरण के लिए, मान लें कि हम पाप के व्युत्पन्न की गणना करना चाहते थे तमाम , इसलिए हम \(f(y) = \sin(y)\) को परिभाषित करते हैं, जहां \(y\) डिग्री में मापा जाता है।

अब, \(x = \frac{\pi y}{180}\) रेडियन में समतुल्य कोण बनें और \(y\) के लिए भी हल करें, हम पाते हैं कि \(y = \frac{180 x}{\pi}\), तो चेन नियम का उपयोग करें:

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

तो इसके आधार पर, डिग्री में साइन का व्युत्पन्न वास्तव में डिग्री में कोसाइन है, लेकिन बार एक कारक \(\frac{180}{\pi}\)।

आप त्रिकोणमिति में डेरिवेटिव कैसे पाते हैं?

बेसिक ट्रिग पहचान का उपयोग करके ट्रिग डेरिवेटिव को परिभाषा से पाया जाता है।उदाहरण के लिए, का उपयोग करना योग rayr की kayna हम सीमा की परिभाषा का उपयोग करके \(\sin(x)\) के व्युत्पन्न को प्राप्त कर सकते हैं:

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

युक्तियाँ और चालें

आपके लिए मुख्य takeaways हमेशा याद दिलाना है कि क्या ६ सराय , और उन्हें दिल से जानते हैं, जैसा कि आप उन्हें मूल के साथ लगातार इस्तेमाल करेंगे विभेदक नियम ।

इसी तरह, आप सबसे आम उलटा ट्रिग डेरिवेटिव खोजने के लिए ट्रिग पहचान और उलटा फ़ंक्शन की परिभाषा का उपयोग कर सकते हैं।

उदाहरण: ट्रिग व्युत्पन्न गणना

निम्नलिखित फ़ंक्शन पर विचार करें: \(f(x) = \sin^2(x)+ \frac{1}{x}\)।इसके व्युत्पन्न का पता लगाएं

तमाम: ट्रिग डेरिवेटिव में ट्रिग फ़ंक्शन शामिल होता है जिसे विभेदित करने की आवश्यकता होती है।फ़ंक्शन पर विचार करें \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\), जिसमें एक साइन फ़ंक्शन होता है, इसलिए यह ट्रिग व्युत्पन्न के रूप में योग्य होता है।

\( \displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2+\frac{1}{x}\right)\)

By using the linearity property, we know \(\frac{d}{dx}\left( \sin(x)^2+\frac{1}{x} \right) = \frac{d}{dx}\left(\sin(x)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)\)

Using the Power Rule for a polynomial term with negative exponent: \(\frac{d}{dx}\left( \frac{1}{x} \right) = -\frac{1}{x^2}\) and in this case we can use the Power Rule for a constant exponent: \(\frac{d}{dx}\left( \sin\left(x\right)^2 \right) = 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\frac{1}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cdot \cos\left(x\right)-\frac{1}{x^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cos\left(x\right)+\frac{-1}{x^2}\)

Directly expanding and simplifying

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\)

शराबी : इस उदाहरण के लिए, यह पाया जाता है कि व्युत्पन्न है:

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

यह एक ग्राफ पर फ़ंक्शन और इसके व्युत्पन्न को चित्रित करने के लिए बहुत उपयोगी है।नीचे देखें:

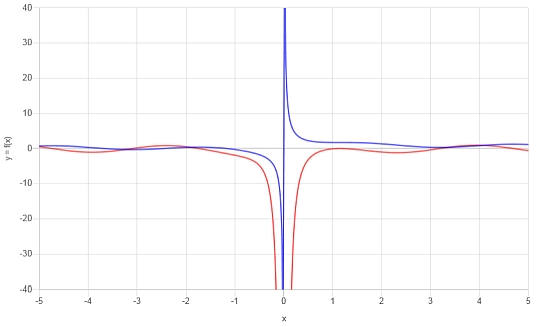
उदाहरण एक ट्रिग फ़ंक्शन के व्युत्पन्न

निम्नलिखित ट्रिग फ़ंक्शन पर विचार करें: \(f(x) = \sin(x) + x \cos(x)\), इसके व्युत्पन्न का पता लगाएं।

तमाम: अब, हमें निम्नलिखित ट्रिग फ़ंक्शन \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\) के व्युत्पन्न के साथ काम करने की आवश्यकता है।

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x\right)+\sin\left(x\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x\cos(x)+\sin(x) \right) = \frac{d}{dx}\left(x\cos(x)\right)+\frac{d}{dx}\left(\sin(x)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\cos\left(x\right)\right)+\frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\) and we can use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)+\cos\left(x\right)\)

By applying direct differentiation: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \left(-\sin\left(x\right)\right)+\cos\left(x\right)\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot \left(-\sin\left(x\right)\right)+\cos\left(x\right)+\cos\left(x\right)\)

We group together the terms that are multiplying \(\cos\left(x\right)\) and then simplifying \(1+1 = 2\)

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot \left(-\sin\left(x\right)\right)+2\cos\left(x\right)\)

By reorganizing the terms:

\( \displaystyle = \,\,\)

\(\displaystyle -x\sin\left(x\right)+2\cos\left(x\right)\)

तमाम : हम निष्कर्ष निकालते हैं कि व्युत्पन्न द्वारा दिया गया है:

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

निम्नलिखित भूखंड प्राप्त किया जाता है:

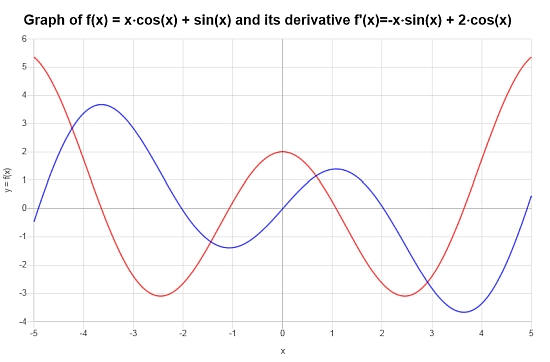
उदाहरण: ट्रिग डेरिवेटिव और अंतर्निहित भेदभाव

\(\frac{dy}{dx}\) के लिए \( \sin(x)+\cos(y) = 1 \) का पता लगाएं।

तमाम: हमें उपयोग करने की आवश्यकता है अँगुला , इसलिए हम दोनों पक्षों को अलग करते हैं और उपयोग करते हैं तिहाई :

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

जो गणना का समापन करता है।

अन्य उपयोगी व्युत्पन्न कैलकुलेटर

वthaumaum -kay सरल और प्राथमिक कार्यों में अच्छी तरह से ज्ञात के उपयोग के माध्यम से अधिक जटिल कार्यों के डेरिवेटिव खोजने की प्रक्रिया की आधारशिला है विभेदन नियम ।

इस संदर्भ में, बुनियादी अफ़्री प्राथमिक कार्य माना जा सकता है जिसके लिए व्युत्पन्न की गणना सीमाओं का उपयोग करके की जा सकती है, इसकी परिभाषा के माध्यम से।हमारे पास सबसे उपयोगी प्राथमिक कार्यों में से तंग और तर्कसंगत कार्य।