समाधानकर्ताओं बीजगणित

क्षैतिज रेखा परीक्षण

निर्देश: क्षैतिज रेखा परीक्षण चलाने के लिए इस कैलकुलेटर का उपयोग करें, जिसमें सभी चरण दिखाए गए हैं। कृपया नीचे दिए गए फॉर्म में वह फ़ंक्शन टाइप करें जिसका आप विश्लेषण करना चाहते हैं।

क्षैतिज रेखा परीक्षण

यह कैलकुलेटर आपको चरण दिखाते हुए आपके द्वारा प्रदान किए गए किसी भी फ़ंक्शन के लिए क्षैतिज रेखा परीक्षण चलाने की अनुमति देगा। आपके द्वारा प्रदान किया जाने वाला फ़ंक्शन कुछ इस तरह हो सकता है 'y = 2x - 1', जो कि सबसे सरल प्रकार है रैखिक प्रकार्य आप पा सकते हैं, या आप 'y = (2x-1)/(x+1)' जैसा अधिक जटिल फ़ंक्शन प्रदान कर सकते हैं जिसमें a शामिल है तर्कसंगत कार्य .

एक बार जब आप एक वैध फ़ंक्शन प्रदान करते हैं, तो आप "गणना करें" बटन पर क्लिक कर सकते हैं, और आपको प्रक्रिया के सभी चरण प्रदान किए जाएंगे, यह इंगित करते हुए कि फ़ंक्शन क्षैतिज रेखा परीक्षण (एचएलटी) पास करता है या नहीं।

जिस तरह से यह कैलकुलेटर काम करता है वह एक सामान्य क्षैतिज रेखा सेट करके होता है, और यह जांचता है कि रेखा कितनी बार (यदि कभी भी) इस दी गई मनमानी क्षैतिज रेखा को पार करती है। इसमें शामिल है एक्स के लिए हल करना समीकरण y = f(x).

क्षैतिज रेखा परीक्षण क्या है?

एचएलटी एक परीक्षण है जो आपको यह आकलन करने की अनुमति देता है कि कोई फ़ंक्शन एक-से-एक है या नहीं। इसमें अलग-अलग ऊंचाई पर क्षैतिज रेखाएं खींचना और यह देखना शामिल है कि वे दिए गए फ़ंक्शन f(x) के ग्राफ़ को कहां पार करते हैं, यदि वे ऐसा करते हैं।

यदि कोई क्षैतिज रेखा जिसकी आप कल्पना कर सकते हैं, फ़ंक्शन f(x) के ग्राफ़ को एक से अधिक बार पार नहीं करेगी, तो फ़ंक्शन एक-से-एक है . दूसरी ओर, यदि आप एक क्षैतिज रेखा ढूंढने में सक्षम हैं जो फ़ंक्शन f(x) के ग्राफ़ को एक से अधिक बार पार करेगी, तो आपने साबित कर दिया है कि फ़ंक्शन एक-से-एक नहीं है

तो फिर आप सोच रहे होंगे "एक मिनट रुकें", यह टूल वास्तव में क्षैतिज रेखा परीक्षण का उपयोग करके यह साबित करने के लिए काम नहीं करता है कि कोई फ़ंक्शन एक-से-एक है, बल्कि यह साबित करने के लिए काम करता है कि इसका उपयोग करके यह एक-से-एक नहीं है .

क्योंकि, व्यावहारिकता में, मैं यह जांचने के लिए सभी क्षैतिज रेखाओं का ग्राफ़ नहीं बना सकता कि वे कितनी बार f(x) के ग्राफ़ को पार करती हैं, लेकिन अगर मुझे एक क्षैतिज रेखा मिलती है जो f(x) के ग्राफ़ को कई बार पार करती है, तब मैं जानता हूं कि यह एक-से-एक नहीं है। तो, अच्छी सोच, आप वहां कुछ अच्छा कर रहे हैं।

व्यावहारिकता में क्षैतिज रेखा परीक्षण का उपयोग करना

उदाहरण के लिए, यदि आपके पास फ़ंक्शन \(f(x) = x^2\) है, तो ग्राफ़ कमोबेश ऐसा दिखेगा:

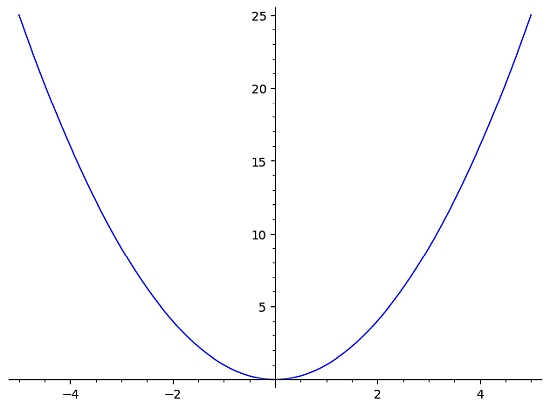
इस मामले में, हम तुरंत देखते हैं कि यह फ़ंक्शन क्षैतिज रेखा परीक्षण में विफल रहता है। क्यों, क्योंकि नीचे दिए गए ग्राफ़ में दिखाई गई क्षैतिज रेखा y = 10 f(x) के ग्राफ़ को दो बार (एक से अधिक बार) काटती है

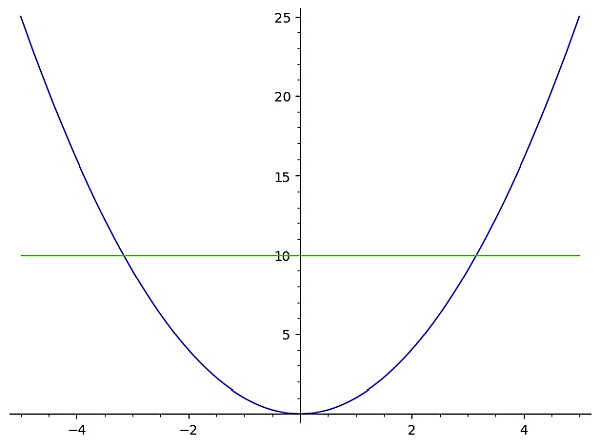
इस मामले में, फ़ंक्शन \(f(x) = x^2\) क्षैतिज रेखा परीक्षण में विफल रहता है और इसलिए, यह नहीं है एक-से-एक कार्य .

अब, चूंकि सभी संभावित क्षैतिज रेखाओं का परीक्षण करना असंभव है, इसलिए एचएलटी को बीजगणितीय साधनों का उपयोग करने का प्रयास करने की आवश्यकता है, जब तक कि आप क्षैतिज रेखा का स्पष्ट मामला नहीं देखते हैं जो फ़ंक्शन को परीक्षण में विफल कर देगा।

क्षैतिज रेखा परीक्षण का उपयोग करना (विश्लेषणात्मक रूप से)

स्टेप 1: किसी दिए गए मान्य फ़ंक्शन f(x) से प्रारंभ करें, आप y के मनमाने मान पर एक क्षैतिज रेखा का स्तर निर्धारित करेंगे
चरण दो: तो आप समीकरण सेट करते हैं: y = f(x), और उद्देश्य x के लिए हल करना है
चरण 3: करने के लिए कोई एक रणनीति नहीं है इस समीकरण को हल करें , क्योंकि यह फ़ंक्शन f(x) की प्रकृति पर निर्भर करता है। यदि f(x) एक सरल रैखिक या द्विघात फलन है, तो x के लिए इसे हल करना काफी आसान है। यदि नहीं, तो विभिन्न तरीकों का परीक्षण करने की आवश्यकता है
चरण 4: यदि x को हल करते समय आपको मनमाने y के लिए एक से अधिक समाधान मिलते हैं, तो फ़ंक्शन HLT को विफल कर देता है। अन्यथा, यदि एक समाधान है या कोई समाधान नहीं है, तो यह उसे पारित कर देता है।

घटाना अंश सिर्फ अंशों के योग से प्राप्त होता है: दो अंशों को घटाने के लिए, आप बस दूसरे को -1 से गुणा करते हैं, और इसे पहले में जोड़ें .

क्या क्षैतिज रेखा ऋणात्मक या धनात्मक मान ले सकती है?

एचएलटी के विश्लेषणात्मक कार्यान्वयन की मुख्य कुंजी यह है कि आप एक मनमानी क्षैतिज रेखा चुनते हैं। यह मनमाना मान हो सकता है, या तो सकारात्मक या नकारात्मक। फिर, उपयोग किए गए y का मनमाना मान यह निर्धारित कर सकता है कि प्रस्तावित समाधान अच्छी तरह से परिभाषित है या नहीं, लेकिन यह अधिक समाधान नहीं जोड़ता है, इसके बजाय संभावित रूप से समाधान घटा सकता है।

उदाहरण के लिए, जब आप \(f(x)= \frac{2x+1}{x-1}\) से शुरू करते हैं, और x के लिए इसे हल करते हैं: \(y = \frac{2x+1}{x-1}\), तो आप पहुंचेंगे

\(x = \frac{y+1}{y-2}\)

जिसका अर्थ है कि किसी दिए गए \(y\) के लिए आपके पास अधिकतम एक ही समाधान है। अधिक से अधिक एक ही समाधान क्यों? क्योंकि जब y = 2 होता है तो वास्तव में कोई समाधान नहीं होता है, और किसी अन्य y के लिए, एक ही समाधान होता है। यह यह दिखाने के लिए बहुत अच्छा काम करता है कि फ़ंक्शन क्षैतिज रेखा परीक्षण पास कर लेता है।

उदाहरण: एचएलटी उत्तीर्ण करना

क्या निम्नलिखित फ़ंक्शन HLT पास करता है: \(f(x) = \frac{1}{3} x + \frac{5}{4}\)?

समाधान:

जो फ़ंक्शन प्रदान किया गया है वह है:

\[f\left(x\right) = \frac13x+\frac54\]

फिर, यह आकलन करने के लिए कि दिया गया फ़ंक्शन क्षैतिज रेखा परीक्षण पास करता है या नहीं, हमें \(x\) को हल करने और यह निर्धारित करने की आवश्यकता है कि क्या कोई समाधान नहीं है, एक समाधान है, या एकाधिक समाधान हैं। प्रारंभिक समीकरण है

\[y=\frac{1}{3}x+\frac{5}{4}\]

रैखिक समीकरण को हल करना

बाएं हाथ की तरफ \(x\) और \(y\) और दाहिने हाथ की तरफ स्थिर

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(-\frac{1}{3}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=3y-\frac{15}{4}\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने पर \(x = 3y-\frac{15}{4}\) प्राप्त होता है।

हमने पाया कि चूंकि \(x\) को हल करते समय हमें एक समाधान मिलता है और यह केवल एक समाधान है, दिया गया फ़ंक्शन क्षैतिज रेखा परीक्षण पास करता है।

क्षैतिज रेखा परीक्षण परिणाम

ऊपर दिखाए गए कार्य के आधार पर, यह निष्कर्ष निकाला जा सकता है कि दिया गया फ़ंक्शन क्षैतिज रेखा परीक्षण पास करता है।

ग्राफिक रूप से, स्थिति को इस प्रकार दर्शाया गया है:

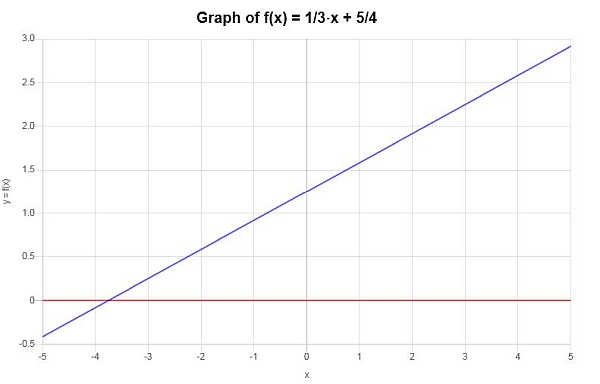
उदाहरण: क्या यह फ़ंक्शन वन-टू-वन है?

क्षैतिज रेखा परीक्षण का उपयोग करके, इंगित करें कि क्या निम्नलिखित फ़ंक्शन एक-से-एक है: \(f(x) = x^3 - 1\)

समाधान: यह आकलन करने के लिए कि दिया गया फ़ंक्शन क्षैतिज रेखा परीक्षण पास करता है या नहीं, हमें \(x\) के लिए समीकरण \(y = x^3 - 1\) को हल करने और यह निर्धारित करने की आवश्यकता है कि क्या कोई समाधान नहीं है, एक समाधान है, या एकाधिक समाधान हैं।

प्रारंभिक चरण: इस मामले में, हमें पहले दिए गए समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

\( \displaystyle y-\left(x^3-1\right) = 0\)

The multiplication by -1 gets distributed as follows: \(-\left(-1+x^3\right) = 1-x^3\)

\( \displaystyle \Rightarrow \,\, \,\,\)

\(\displaystyle y+1-x^3 = 0\)

\( \displaystyle -x^3+y+1 = 0\)

Keeping the term with \(x\) on one side and the rest on the other side

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,-x^3 = -y-1\)

Multiplying both sides of the equation by -1

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x^3 = y+1\)

Cancelling the cubed power on the variable x

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x=\left(y+1\right)^{\frac{1}{3}}, \,\,x=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right), \,\,x=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right)\)

फिर, हमें समाधान मिलते हैं:

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

इन समाधानों में से, हमारे पास केवल एक ही वास्तविक समाधान है, जो \(x_1=\left(y+1\right)^{\frac{1}{3}}\) है। इसलिए, और चूंकि \(x\) को हल करते समय हमें एक समाधान मिलता है और यह केवल एक वास्तविक समाधान है, दिया गया फ़ंक्शन क्षैतिज रेखा परीक्षण पास करता है।

                                    
                                        क्षैतिज रेखा परीक्षण परिणाम
                                    
                                    Based on what was found above, it can be concluded that the given function passes the Horizontal Line Test.