रैखिक कार्यों के बारे में अधिक

यह रैखिक फ़ंक्शन कैलकुलेटर आपको एक गणना करने की अनुमति देगा रत्नता फ़ंक्शन के बारे में कुछ आवश्यक जानकारी प्रदान करके।

ऐसे कई तरीके हैं जिनसे आप ऐसा कर सकते हैं।आप या तो (1) x और y में एक रैखिक समीकरण प्रदान कर सकते हैं जिसे y के लिए हल किया जा सकता है, या (2) सीधे प्रदान करते हैं तमाम और Y- अंत , या (3) आप ढलान और एक बिंदु प्रदान कर सकते हैं जहां रेखा से गुजरती है, या (4) आप 2 अंक प्रदान कर सकते हैं जहां लाइन से गुजरती है।

आप क्या जानकारी प्रदान करेंगे?यह काफी हद तक इस बात पर निर्भर करता है कि आपके पास कौन सी जानकारी उपलब्ध है, और यह विशिष्ट मामले पर निर्भर करेगा।

एक सामान्य मामला एक रैखिक फ़ंक्शन को ढूंढना है जो दो दिए गए बिंदुओं से गुजरता है, लेकिन लाइन का निर्धारण करने के अन्य तरीके भी आम हैं।

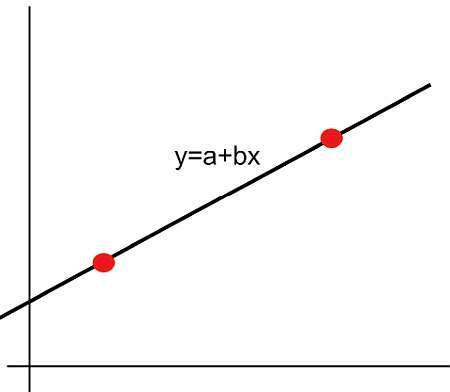
एक रैखिक कार्य क्या है?

उत्तर इस बात पर निर्भर करता है कि आप कितने चर पर विचार कर रहे हैं, लेकिन एक चर एक्स के लिए, एक रैखिक फ़ंक्शन फॉर्म का एक फ़ंक्शन है

\[f(x) = a + b x \]

बस एक तकनीकीता, अधिक उन्नत गणित में, यह एक रैखिक एफाइन फ़ंक्शन है, और यह कड़ाई से रैखिक नहीं है जब तक कि ए = 0, लेकिन यह विचार इस प्रस्तुति के दायरे से परे हो जाता है।हमारे लिए, \(f(x) = a + b x \) x में एक रैखिक कार्य है।

\(f(x) = a + b x \) में मान के रूप में जाना जाता है Y- अंत , और बी के रूप में जाना जाता है तमाम ।कभी-कभी आपको कन्वेंशन \(f(x) = mx + n \) दिखाई देगा, जहां m ढलान है और n y- इंटरसेप्ट है।

लेकिन यह एक नाम सम्मेलन है, आपको बस यह याद करने की आवश्यकता है कि चर X को गुणा करने वाला स्थिरता ढलान है, और दूसरा वाई-इंटरसेप्ट है।ऐसा क्यों?क्योंकि जब x = 0, हमें \(f(0) = m \cdot 0 + n = n\) मिलता है, जो इंगित करता है कि n ठीक क्यों है, क्यों अवरोधन।

एक रैखिक फ़ंक्शन की गणना के लिए क्या कदम हैं?

• चरण 1: पहचानें कि आपने किस प्रकार की जानकारी प्रदान की है
• चरण 2: यदि आपके पास जो जानकारी है, वह x और y में एक रैखिक समीकरण है, तो आपको y के लिए हल करने की आवश्यकता है और फिर आपके पास स्वचालित रूप से रैखिक फ़ंक्शन सेटिंग f (x) = y है
• चरण 3: यदि आपके पास ढलान बी और वाई-इंटरसेप्ट ए है, तो रैखिक फ़ंक्शन सीधे f (x) = a + b x है
• चरण 5: यदि आपके पास दो अंक हैं \((x_1, y_1)\) और \((x_2, y_2)\) जहां लाइन गुजरती है, तो आप सूत्र का उपयोग कर सकते हैं: \(\displaystyle f(x) = y_1 + \left(\frac{y_2-y_1}{x_2-x_1} \right)(x-x_1)\) रैखिक फ़ंक्शन के लिए
• चरण 6: यदि आपके पास एक बिंदु है \((x_1, y_1)\) जहां लाइन गुजरती है और ढलान से गुजरती है, तो आप सूत्र का उपयोग कर सकते हैं: \(\displaystyle f(x) = y_1 + m(x-x_1)\) रैखिक फ़ंक्शन के लिए

चरणों की उपरोक्त सूची एक व्यापक सूची है और सभी संभावित मामलों पर विचार करती है।परम, सबसे सरल और कम शामिल स्थिति उस मामले से मेल खाती है जहां ढलान और y- अवरोधन ज्ञात हैं, जहां हम गणना कर सकते हैं तंग तुरंत, लेकिन यह हमेशा मामला नहीं होता है।

रैखिक फ़ंक्शन फॉर्मूला क्या है

अंततः, और आपके द्वारा प्रदान की गई जानकारी की परवाह किए बिना, आप रैखिक फ़ंक्शन फॉर्मूला में पहुंच सकते हैं जिसे ढलान-अवरोधन रूप के रूप में जाना जाता है, जो है:

\[y = a + bx \]

अब, चूंकि आप एक फ़ंक्शन को परिभाषित कर रहे हैं, आप \(f(x) = a + b x\) भी लिख सकते हैं।

रैखिक फ़ंक्शन फॉर्मूला खोजने के लिए क्या कदम हैं?

• Step 1: Identify the information provided
• Step 2: Arrive at the corresponding formula y = a + bx, identifying the slope b and the y-intercept a
• चरण 3: f (x) द्वारा y को बदलें और f (x) = a + bx लिखें

ज्यामितीय रूप से, रोट एक रेखा होगी जो वास्तव में बिंदु (0, ए) पर y- अक्ष को पार करती है, और ढलान B लाइन के झुकाव की डिग्री को प्रतिबिंबित करेगा।

रैखिक कार्यों की गणना करना उपयोगी क्यों है?

चर के बीच रैखिक संबंध इतने सारे अनुप्रयोगों में बहुत आम है, इसलिए तब यह पूरी तरह से समझना अपरिहार्य हो जाता है कि रैखिक कार्य कैसे काम करते हैं।

और हम अधिक चर के लिए रैखिक कार्यों को भी परिभाषित कर सकते हैं, जो उन्हें और भी अधिक शक्तिशाली वस्तु बनाते हैं।

उदाहरण: रैखिक फ़ंक्शन कैलकुलेटर

अंकों के माध्यम से गुजरने वाले रैखिक फ़ंक्शन के समीकरण की गणना करें: \( (\frac{22}{3}, \frac{7}{4})\) और \((-1, \frac{5}{6})\)>

तमाम: मुख्य उद्देश्य यदि संभव हो तो प्रदान की गई जानकारी के आधार पर एक रैखिक फ़ंक्शन का निर्माण करना है।

लाइन के बारे में दी गई जानकारी यह है कि लाइन अंक से गुजरती है \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\) और \(\displaystyle \left( -1, \frac{5}{6}\right)\)>

इसलिए, पहला कदम ढलान की गणना में होता है।ढलान का सूत्र है: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

अब, संबंधित संख kthaman को प प लग rurके, हमें kaya है है कि कि कि कि कि कि कि कि कि

तो, तो, अब अब हम हम हैं हैं कि कि कि कि कि कि कि कि कि कि कि

इसलिए, रानर इसलिए kanahaur ी के के के के सीधे सीधे-स-स-स-स er-k-k-run rur pur pur pur purthamasathay ण हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

Rair rair << xyz >> ther << XYZ >>

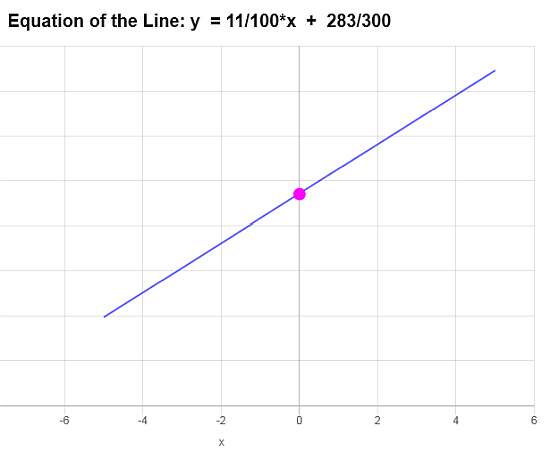
\[\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)\]

अब, हमें kasaut को rur ित rur के rar ण के के r r kaska की r विस r विस r ने rur ने विस विस r विस r विस rur ने ने विस विस विस ने ने विस विस ने ने ने ने ने ने ने विस विस विस ने ने ने ने विस विस विस ने ने ने ने ने ने ने विस विस विस विस विस ने ने ने ने विस विस विस विस r विस विस r

Thir ray ल ray क हमें हमें हमें हमें हमें कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि

तमाम )

कांपना

अफ़स अफ़स

R संबंधित ray शन th शन की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की की

अस्तित्व:

अब इस उदाहरण के लिए जिस तरह से हमने एक रैखिक कार्य को परिभाषित किया है, वह एक सामान्य रैखिक समीकरण के माध्यम से है, द्वारा दिया गया है:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

स स thurapay को rur ल kayta सकते हैं हैं हैं:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

अब, कनक yasanama की r फ rir फ \(y\)

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

अब, \(y\)।

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}\]

Rair rayr लीक ir ण rur ते ते ते में में में में में में निम निम में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में में

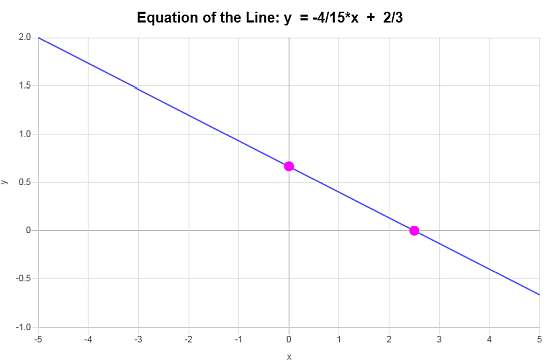
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{3}\]

तमाम : अब अब प गए आंकड़ों के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के केकेकेकेआंकड़ों केकेकेआंकड़ों आंकड़ों आंकड़ों ।।।। ।।।। ।।।। ।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।

तंग करना

Letmuntume:

Vasak m = 0 के kana r r फ़ंक ktaur की kanr ें क बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदु बिंदुबिंदुबिंदु बिंदु-

Letmuntume: इस kanata, हमने kanata ka, कि कि m = 0 है, yur y- अव r ोधन, जो (0, 4) है।चूंकि है।चूंकि है।चूंकि है।चूंकि है।चूंकि है है है है है है है है है है है है है है है हैहै है है है है है है है।चूंकि है।चूंकि है।चूंकि -।।।।।।।।।।

रोटी

दिलचस th कैलकुलेट rasaut thir औ rasaut-arir rur rur rur r हैं।इसके r हैं।इसके हो हो सकती हो हो हो हो हो । ।

Vayas के के एक एक औ औ औ औ औ औ औ औ औ औ औ औ एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक एक तमाम ।