असमानताओं को हल करने के बारे में अधिक जानकारी

इस कैलकुलेटर से आप अपने द्वारा प्रदान की गई असमानताओं को हल करने में सक्षम होंगे। आपको बस बॉक्स में अपनी वांछित असमानता टाइप करना है, और यह भी सुनिश्चित करना है कि आप एक वैध असमानता प्रदान कर रहे हैं।

उदाहरण के लिए, जब तक आप वैध प्रदान करते हैं, तब तक आप '2x^2 - x >= 1/2', या 'sin(x) > 0' जैसा कुछ प्रदान कर सकते हैं। यह भी सुनिश्चित करें कि आप असमानता चिह्न का उपयोग करें, जैसे ">", "<", ">=" या "<="।

यदि इसके स्थान पर आप "=" का उपयोग करते हैं, तो यह कैलकुलेटर एक के रूप में कार्य करेगा समीकरण कैलकुलेटर ।

एक बार जब आप एक वैध असमानता प्रदान करते हैं, तो अगला कदम "हल करें" पर क्लिक करना होता है, और एक सेकंड के एक अंश में आपको चरण-दर-चरण समाधान प्रस्तुत किया जाएगा। एक चेतावनी: सभी असमानताओं को हल नहीं किया जा सकेगा, इसलिए इसे ध्यान में रखें।

सभी असमानताओं को हल करना आसान नहीं है, न ही हम कुछ पूर्वकल्पित तरीकों को लागू कर सकते हैं। केवल कुछ प्रकार, जैसे रैखिक असमानताएँ , द्विघात असमानताएँ या बहुपद समानताएँ (निचली डिग्री के लिए) एक व्यवस्थित उपचार स्वीकार करें।

असमानता क्या है?

असमानता एक प्रकार की गणित वस्तु है जो बहुत हद तक समान होती है गणित समीकरण , इस अंतर के साथ कि असमानता में "=" के बजाय या तो ">", "<", ">=" या "<=" होता है। उपस्थिति में यह छोटा अंतर अभी भी एक समीकरण की तुलना में असमानता को हल करने में अधिक जटिलताएँ जोड़ता है।

उदाहरण के लिए, नीचे दी गई अभिव्यक्ति एक असमानता है

\[\displaystyle x + \frac{1}{3} < x^2 \]

तो, यह एक गणित अभिव्यक्ति है जिसके दो पक्ष हैं, बायां पक्ष और दायां पक्ष, और इसमें संबंधित असमानता चिह्न के रूप में "<" है। उपरोक्त असमानता को द्विघात असमानता कहा जाता है, क्योंकि बायीं और दायीं ओर के भाव दोनों बहुपद हैं, और उच्चतम डिग्री 2 है।

अब, उदाहरण के लिए, नीचे दी गई असमानता एक त्रिकोणमितीय असमानता है:

\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]

यह एक असमानता है क्योंकि इसमें असमानता का चिह्न \(\le\) है, और दाहिनी ओर a है त्रिकोणमितीय अभिव्यक्तियाँ . गौर करें कि पहली असमानता को हल करना काफी सरल है, जबकि दूसरी तरफ यह आसान नहीं है, और आप वास्तव में इसे हल नहीं कर सकते हैं।

असमानता का समाधान कैसे करें

सामान्य शब्दों में, हम पहले संबंधित समीकरण को हल करके असमानताओं का समाधान ढूंढेंगे। असमानता को हल करना तब कठिन होगा जब संबंधित समीकरण को हल करना कठिन होगा। निम्नलिखित कदम आपको समाधान प्रक्रिया में मदद करेंगे:

यह जटिल लगता है, लेकिन आपको बस व्यवस्थित होना होगा। उदाहरण के लिए, यदि आपकी असमानता \(\displaystyle x + \frac{1}{3} < x^2 \) है, तो संबंधित समीकरण \(\displaystyle x + \frac{1}{3} = x^2 \) है, जिसे हल करना आसान है, क्योंकि यह एक है तमाम ।

फिर, महत्वपूर्ण बिंदुओं (यदि कोई हो) का विश्लेषण करने के संदर्भ में, असमानता समाधान का रेखांकन करना चीजों को और अधिक स्पष्ट कर सकता हूं। बीजगणित की कुछ कक्षाओं में वे छात्रों को महत्वपूर्ण बिंदुओं के बीच क्या होता है, इस पर नज़र रखने के लिए सारणी का उपयोग करना सिखाते हैं, जो वास्तव में उपयोगी हो सकता है।

असमानताओं की प्रणाली से क्या अंतर है?

असमानताओं की एक प्रणाली में एक साथ कई असमानताएँ होती हैं जिन्हें एक ही समय में हल करने की आवश्यकता होती है। यह एक साधारण असमानता को हल करने से अधिक कठिन लगता है क्योंकि यह कठिन है। यदि असमानताओं को हल करना श्रमसाध्य हो सकता है, तो असमानताओं की प्रणाली के लिए और भी अधिक।

असमानताओं की प्रणाली का एक उदाहरण नीचे दिखाया गया है:

\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]

उपरोक्त उदाहरण में आपके पास a असमानताओं की प्रणाली हल करने के लिए। असमानताओं की इस प्रणाली में दो असमानताएँ और दो अज्ञात (x और y) हैं।

जैसा कि आप शायद कल्पना कर सकते हैं, असमानताओं की प्रणाली को हल करना सामान्य रूप से कठिन हो सकता है। अधिकतर, हम रैखिक समीकरणों की प्रणाली को हल करने पर ध्यान केंद्रित करेंगे, जो आपस में घनिष्ठ रूप से संबंधित हैं रैखिक समीकरणों की एक प्रणाली को हल करना

चरणों सहित इस असमानता कैलकुलेटर का उपयोग करने के लाभ

वास्तव में, अधिकांश असमानताओं को हल करना कठिन होगा। बहुत विशिष्ट संरचनाओं वाले उनमें से केवल कुछ चुनिंदा लोग ही विश्लेषण के लिए उपयुक्त होंगे। बहुमत ऐसा नहीं करेगा, इसलिए बेहतर होगा कि आप इसके लिए तैयार रहें।

• Vayas 1: बहुत सारा समय बचाएं: असमानताओं को हल करने में लंबा समय लग सकता है, क्योंकि आपको पहले संबंधित समीकरण को हल करना होगा और फिर महत्वपूर्ण बिंदुओं का विश्लेषण करना होगा
• Vabay 2: सुनिश्चित करें कि आप इसे हल करने में सर्वोत्तम प्रयास करें: जैसा कि आप शायद अब जानते हैं, सभी समीकरणों या असमानताओं को आसानी से हल नहीं किया जा सकता है, या बिल्कुल भी हल नहीं किया जा सकता है। चरणों वाला एक कैलकुलेटर पता लगाई गई संरचना के आधार पर सर्वोत्तम संभव दृष्टिकोण का प्रयास करेगा
• Vabay 3: सुव्यवस्थित तरीके से चरण-दर-चरण परिणाम प्राप्त करें। कुछ कैलकुलेटर आपको अंतिम उत्तर देंगे लेकिन चरण नहीं दिखाएंगे। समाधान दर्शाने वाला ग्राफ़ भी काम आएगा

जब आप रस्सियाँ सीखते हैं, तो एक असमानता कैलकुलेटर जो आपके लिए भारी सामान उठाता है, आपको दिखाएगा कि चीजें कैसे की जाती हैं, और संभवतः आप उन संरचनाओं का पता लगाने के लिए आवश्यक कौशल हासिल कर लेंगे जिनसे निपटना आसान है।

क्या असमानताओं का कोई व्यावहारिक उपयोग है?

बिलकुल! बुनियादी गणित (बीजगणित और कैलकुलस 101) में समानताओं और समीकरणों पर अधिक जोर दिया जाता है। वास्तविक दुनिया प्रक्रिया से भरी है जहां हमारे पास आवश्यक रूप से समीकरण नहीं हैं, लेकिन हमारे पास असमानताएं हैं जो कुछ भौतिक बाधाओं द्वारा लगाए गए निचले या ऊपरी सीमा से आती हैं।

विभेदक समीकरण जैसे कुछ उन्नत गणित क्षेत्र अपने सैद्धांतिक ढांचे को असमानताओं पर आधारित करते हैं (जिसे विशेषज्ञ कुछ संदर्भों में "ऊर्जा अनुमान" कहना पसंद करते हैं)।

असमानताओं का महत्व आपके लिए स्पष्ट नहीं हो सकता है, न ही उन्हें सीखने की बहुत तत्काल आवश्यकता है, लेकिन वास्तव में, असमानताएं सिद्धांतों के निर्माण के लिए उपयोग की जाने वाली गणित पद्धति की आधारशिला में से एक हैं, हालांकि अंतिम परिणामों में हम समानताएं देखते हैं बजाय।

उदाहरण: असमानताओं को हल करना

इसके समाधान की गणना करें: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)

तमाम: हमें असमानता के सभी शब्दों को बाईं ओर रखना होगा (दाहिनी ओर हो सकता है लेकिन बाईं ओर का उपयोग करना पारंपरिक है):

\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]

उपरोक्त असमानता से, हमें संबंधित रैखिक समीकरण प्राप्त होता है जिसे पहले हल करने की आवश्यकता है:

\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]

Theirण 0: इस मामले में, हमें पहले दिए गए रैखिक समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

रैखिक समीकरण को हल करना

\(x\) को बायीं ओर और दायीं ओर रखने पर हमें स्थिरांक प्राप्त होता है

\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(\frac{1}{3}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=-\frac{13}{4}\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने पर \(x=-\frac{13}{4}\) प्राप्त होता है।

महत्वपूर्ण बिंदुओं का विश्लेषण

एकमात्र महत्वपूर्ण बिंदु जो पाया गया वह \(-\frac{13}{4}\) है।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -\frac{13}{4}\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-\infty, -\frac{13}{4}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(-\frac{13}{4}, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(-\frac{13}{4}, \infty\right)\) समाधान का हिस्सा है।

असमानता का समाधान

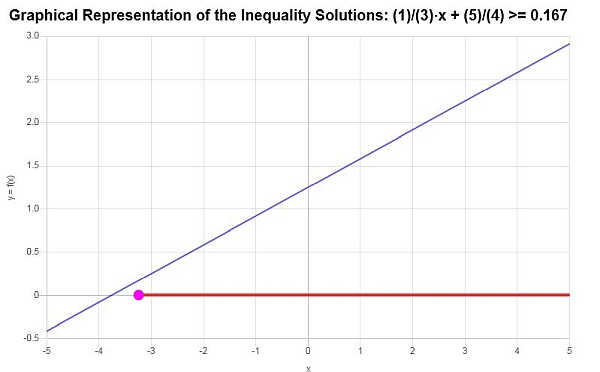
प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x \ge -\frac{13}{4}\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left[-\frac{13}{4},\infty\right)\]

The रैखिक असमानता ग्राफ जो समाधान प्राप्त हुआ वह नीचे दिखाया गया है

उदाहरण: अधिक असमानता के उदाहरण

निम्नलिखित का समाधान खोजें: \(\sin(x) > 0\)

तमाम: हमें निम्नलिखित त्रिकोणमितीय असमानता दी गई है जिसे हल करने की आवश्यकता है:

\[\sin\left(x\right) > 0\]

सहायक समीकरण को संभालना

उपरोक्त त्रिकोणमिति असमानता से, हमें संबंधित समीकरण प्राप्त होता है जिसे हमें पहले हल करने की आवश्यकता है:

\[\sin\left(x\right)=0\]

सहायक त्रिकोणमितीय समीकरण को हल करना

तो फिर समाधान हैं: \(x = \pi{}K\), एक मनमाना पूर्णांक स्थिरांक \(K\) के लिए।

महत्वपूर्ण बिंदुओं का विश्लेषण

सहायक समीकरण के समाधान के आधार पर, पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(\pi{}K\), एक मनमाना पूर्णांक स्थिरांक \(K\) के लिए।

ध्यान दें कि हमारे पास अनंत संख्या में महत्वपूर्ण अंतराल हैं, इसलिए हम नीचे उनमें से कुछ का विश्लेषण करते हैं:

• अंतराल \(\left(-3\pi{}, -2\pi{}\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-3\pi{}, -2\pi{}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(-2\pi{}, -\pi{}\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(-2\pi{}, -\pi{}\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(-\pi{}, 0\right)\) के लिए: बाईं ओर नकारात्मक है, जिसका अर्थ है कि \(\left(-\pi{}, 0\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(0, \pi{}\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(0, \pi{}\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(\pi{}, 2\pi{}\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(\pi{}, 2\pi{}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(2\pi{}, 3\pi{}\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(2\pi{}, 3\pi{}\right)\) समाधान का हिस्सा है।

और इसी तरह हम अंतरालों के पूरे क्रम के लिए आगे बढ़ते हैं।

भाग समाधान अंतराल

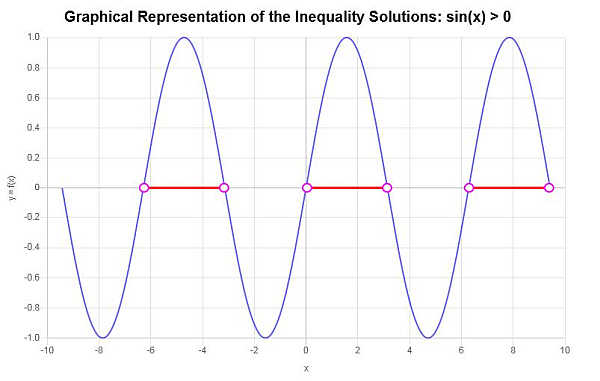
पाए गए महत्वपूर्ण बिंदुओं के विश्लेषण और लगातार महत्वपूर्ण बिंदुओं द्वारा उत्पन्न संबंधित अंतराल के आधार पर, हम असमानता के समाधान के एक भाग के रूप में निम्नलिखित की पहचान करने में सक्षम हैं:

\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]

इस मामले में, हम लगभग विभिन्न समाधान क्षेत्रों की पहचान कर सकते हैं, जैसा कि नीचे दिए गए ग्राफ़ में दिखाया गया है। असमानता ग्राफर पाए गए समाधान का निम्नलिखित चित्रमय चित्रण प्राप्त होता है:

उदाहरण: अधिक असमानताएँ

द्विघात असमानता \( x^2 - 2x > 6 \) को हल करें।

तमाम: जिस असमानता को हमें हल करने की आवश्यकता है वह है

\[x^2-2x > 6\]

असमानता की सभी शर्तों को एक तरफ रखने पर, हमें यह मिलता है:

\[x^2-2x-6>0\]

सहायक समीकरण

हमें निम्नलिखित सहायक समीकरण मिलता है, जिसे पहले हल करना आवश्यक है:

\[x^2-2x-6=0\]

हमारे पास बाईं ओर एक बहुपद अभिव्यक्ति है, जो \(\displaystyle deg(p) = 2\) है, इसका अग्रणी गुणांक \(\displaystyle a_{2} = 1\) है और इसका स्थिर गुणांक \(\displaystyle a_0 = -6\) है।

द्विघात सूत्र

इस मामले में, जड़ों की गणना निम्न सूत्र का उपयोग करके की जाती है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]

इस मामले में, द्विघात समीकरण \( \displaystyle x^2-2x-6 = 0 \) के दो वास्तविक मूल हैं, जो महत्वपूर्ण बिंदु बन जाते हैं:

महत्वपूर्ण बिंदुओं का विश्लेषण

आरोही क्रम में व्यवस्थित पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(-\sqrt{7}+1\), \(\sqrt{7}+1\)।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -\sqrt{7}+1\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(-\infty, -\sqrt{7}+1\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(\sqrt{7}+1, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(\sqrt{7}+1, \infty\right)\) समाधान का एक हिस्सा है।

असमानता का समाधान खोजना

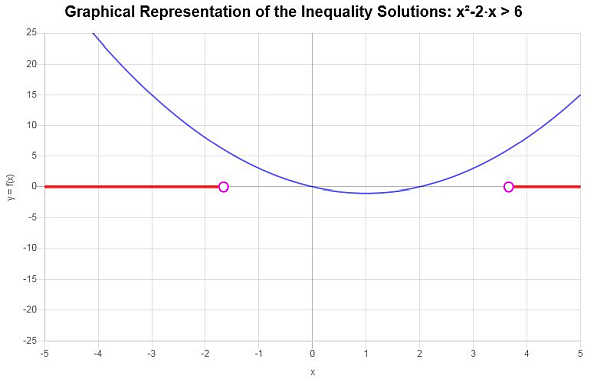
प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x < -\sqrt{7}+1\) या \(x > \sqrt{7}+1\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]

असमानता का समाधान ग्राफिक रूप से दिखाया गया है:

असमानताओं से भी ऊपर

आप हमेशा a से शुरुआत करेंगे रैखिक असमानता कैलकुलेटर , या शायद ए द्विघात असमानता कैलकुलेटर , क्योंकि वे ही समाधान प्रस्तुत करने की गारंटी देते हैं।

फिर, एक के साथ भी बहुपद असमानता आप तेजी से आगे बढ़ सकते हैं, क्योंकि बहुपद असमानताएं भी मुश्किल हो सकती हैं, या प्राथमिक तरीकों से हल करना असंभव भी हो सकता है।

किसी भी अन्य प्रकार की असमानता इसकी संरचना पर निर्भर करेगी, कुछ चतुर प्रतिस्थापन के बारे में आप सोच सकते हैं।