समाधानकर्ताओं बीजगणित

एक-से-एक कार्य

निर्देश: सभी चरणों को दिखाते हुए एक-से-एक फ़ंक्शन का परीक्षण करने के लिए इस कैलकुलेटर का उपयोग करें। कृपया नीचे दिए गए बॉक्स में वह फ़ंक्शन टाइप करें जिसे आप चेक करना चाहते हैं।

एक-से-एक कार्य

यह कैलकुलेटर आपको सभी चरणों को दिखाते हुए यह आकलन करने की अनुमति देगा कि कोई फ़ंक्शन एक-से-एक है या नहीं। पहली चीज़ जो आपको करने की ज़रूरत है वह है फ़ंक्शन प्रदान करना। यह कुछ सरल, रैखिक या द्विघात हो सकता है जैसे 'y = x^2 - 1', या आप इसके लिए जाने का निर्णय ले सकते हैं तर्कसंगत कार्य जैसे 'f(x) = (x-1)/(x+3)'.

फिर, हम आपने जो प्रदान किया है उससे संतुष्ट हैं और आपने यह सुनिश्चित कर लिया है कि फ़ंक्शन वैध है, आप "गणना करें" बटन पर क्लिक करें, ताकि प्रक्रिया के सभी चरण आपको दिखाए जा सकें।

बीजगणित और कैलकुलस में एक-से-एक फ़ंक्शन की अवधारणा बहुत महत्वपूर्ण है। एक-से-एक परीक्षण करने के कई सरल तरीके हैं, उनमें से एक है क्षैतिज रेखा परीक्षण , लेकिन इसकी प्रकृति के कारण, इसका उपयोग यह साबित करने के लिए करना आसान है कि कोई फ़ंक्शन एक-से-एक है। यह साबित करने के लिए कि कोई फ़ंक्शन एक-से-एक है, हमें एक की आवश्यकता है समीकरण हल करना , विश्लेषणात्मक प्रक्रिया।

वन-टू-वन प्रक्रिया क्या है

सीधे शब्दों में कहें तो, एक-से-एक या इंजेक्टिव फ़ंक्शन वह है जो दो अलग-अलग \(x_1\) और \(x_2\) के लिए, \(f(x)\) के माध्यम से उनकी छवियों का मान अलग-अलग होता है, जिसका गणितीय अर्थ होता है

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

कुछ प्रशिक्षक इसे थोड़ा अलग तरीके से लिखना पसंद करते हैं, लेकिन फिर भी समान तरीके से: फ़ंक्शन एक-से-एक है यदि

\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]

यह एक परिष्कृत तरीके से कह रहा है कि, यदि फ़ंक्शन का ग्राफ़ समान मान (एक क्षैतिज रेखा) को पार करता है, तो ऐसा तभी होता है जब बिंदु समान होता है। तो, आप सब यह कह रहे हैं कि ऐसे दो अलग-अलग बिंदु नहीं हैं जहां एक क्षैतिज रेखा इसे काटती है। तो, आप बस यही दोहरा रहे हैं क्षैतिज रेखा परीक्षण .

कैसे जांचें कि कोई फ़ंक्शन वन-टू-ने है या नहीं

स्टेप 1: मूल फ़ंक्शन f(x) से प्रारंभ करें, और समीकरण y = f(x) सेट करें
चरण दो: x के लिए हल करने का प्रयास करें
चरण 3: यदि आपको एक से अधिक समाधान मिलते हैं, तो फ़ंक्शन एक-से-एक नहीं है, और यदि इसका एक समाधान है या कोई समाधान नहीं है, तो फ़ंक्शन एक-से-एक है

आम तौर पर, आप यह सुनिश्चित करने के लिए कुछ बुनियादी निरीक्षण करेंगे कि वह फ़ंक्शन स्पष्ट रूप से एक-से-एक नहीं है, संभवतः इसलिए क्योंकि आप एचएलटी को विफल करने के लिए आसानी से एक क्षैतिज रेखा पा सकते हैं।

फिर, आप कुछ बुनियादी दृश्य गुणों की तलाश करेंगे: क्या फ़ंक्शन हमेशा बढ़ रहा है (तब यह एक-से-एक है), और यही बात उस स्थिति में भी लागू होती है जहां फ़ंक्शन हमेशा घट रहा है।

एक-से-एक का व्युत्क्रम ज्ञात करने से क्या संबंध है?

सरल शब्दों में कहें तो, किसी फ़ंक्शन का व्युत्क्रम ज्ञात करने के लिए, फ़ंक्शन को एक-से-एक होना चाहिए, कम से कम एक निश्चित उप-डोमेन पर। कई बार हम डोमेन को प्रतिबंधित करते हैं इसलिए हम प्रतिबंधित डोमेन में एक फ़ंक्शन को 1-टू-1 बनाते हैं, अन्यथा यह 1-टू-1 नहीं होता।

उदाहरण के लिए, \(f(x) = x^2\) कुल मिलाकर एक-से-एक नहीं है। क्यों, क्योंकि आप दो अलग-अलग बिंदु \(x_1 = -1\) और \(x_2 = 1\) ले सकते हैं और पा सकते हैं कि \(f(x_1) = (-1)^2 = 1\) और \(f(1) = 1^2 = 1\), जिसका अर्थ है कि संपत्ति (एक-से-एक लक्षण वर्णन)

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

संतुष्ट नहीं है. अब, यदि पूर्ण वास्तविक रेखा \(\R\) पर विचार करने के बजाय, हम केवल सकारात्मक मानों पर विचार करते हैं, तो हम यह निष्कर्ष निकाल सकते हैं कि फ़ंक्शन सकारात्मक वास्तविक मानों पर एक-से-एक है (संकेत: उस उपडोमेन पर, फ़ंक्शन बढ़ रहा है)

क्या यह आकलन करने का कोई सूत्र है कि कोई फ़ंक्शन एक-से-एक है या नहीं?

दुर्भाग्य से नहीं। मेरा मतलब है, कोई \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \) को एक-से-एक सूत्र के रूप में सोच सकता है, लेकिन यह एक सूत्र के बजाय एक तार्किक स्थिति है।

हालाँकि, एक बहुत व्यापक, सामान्य प्रक्रिया है जिसका उपयोग यह परीक्षण करने के लिए किया जाता है कि कोई फ़ंक्शन एक-से-एक है या नहीं, जिसे आप ऊपर वर्णित देख सकते हैं। कोई "एक-से-एक फॉर्मूला" नहीं है। यदि हमें किसी एक पर समझौता करना है, तो यह y = f(x) होना चाहिए।

और, हम सिर्फ x के लिए हल करते हैं। न कुछ ज्यादा, न कुछ कम। अंततः, यह इस बात पर निर्भर करेगा कि f(x) क्या है। एक बहुत ही जटिल, जटिल फ़ंक्शन को हल करने में बहुत सारी कठिनाइयाँ आ सकती हैं, और शायद आपको इसके लिए एक फ़ंक्शन कैलकुलेटर की आवश्यकता है, और एक फ़ंक्शन कैलकुलेटर के साथ भी आप असफल हो सकते हैं।

आप शायद सोच रहे होंगे, ऐसा क्यों?? ऐसा इसलिए है, क्योंकि इसके मूल में, हमारे पास सभी समीकरणों को हल करने की तकनीक नहीं है। हम कुछ विशिष्ट प्रकार के समीकरणों के साथ बस वही करते हैं जो हम कर सकते हैं, लेकिन हम सभी समीकरणों को हल करने का सटीक तरीका जानने से बहुत दूर हैं।

उदाहरण: वन-टू-वन फ़ंक्शन

निम्नलिखित फ़ंक्शन इंजेक्टिव है: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)

समाधान:

हमें निम्नलिखित फ़ंक्शन प्रदान किया गया है:

\[f(x) = \frac{1}{4} x + \frac{5}{4}\]

फिर, यह आकलन करने के लिए कि दिया गया फ़ंक्शन एक-से-एक है या नहीं, हमें \(x\) को हल करने और यह निर्धारित करने की आवश्यकता है कि क्या कोई समाधान नहीं है, एक समाधान है, या एकाधिक समाधान हैं। प्रारंभिक समीकरण है

\[y=\frac{1}{4}x+\frac{5}{4}\]

बाएं हाथ की तरफ \(x\) और \(y\) और दाहिने हाथ की तरफ स्थिर

\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(-\frac{1}{4}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=4y-5\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने से \(x=4y-5\) प्राप्त होता है और यह केवल एक वास्तविक समाधान है, इसलिए दिया गया फ़ंक्शन एक-से-एक है।

निष्कर्ष

पिछले अनुभाग में जो पाया गया है उसके आधार पर, यह निष्कर्ष निकाला जा सकता है कि दिया गया फ़ंक्शन एक-से-एक है।

रेखांकन:

उदाहरण: 1-टू-1 फ़ंक्शन

सिद्ध या असिद्ध करें कि निम्नलिखित फ़ंक्शन एक-से-एक है: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)

समाधान: यह आकलन करने के लिए कि दिया गया फ़ंक्शन एक-से-एक है या नहीं, हमें \(x\) को हल करने और यह निर्धारित करने की आवश्यकता है कि क्या कोई समाधान नहीं है, एक समाधान है, या एकाधिक समाधान हैं। हमें जिस प्रारंभिक समीकरण का उपयोग करने की आवश्यकता है वह है:

\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]

प्रारंभिक चरण: इस मामले में, हमें पहले दिए गए समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

\( \displaystyle y-\left(\frac{1}{3}x^2-5x-\frac{5}{6}\right) = 0\)

Multiplying by -1: \(-\left(\frac{-5}{6}+\frac{1}{3}x^2-5x\right) = \frac{5}{6}-\frac{1}{3}x^2+5x\)

\( \displaystyle \Rightarrow \,\, \,\,\)

\(\displaystyle y+\frac{5}{6}-\frac{1}{3}x^2+5x = 0\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle \Rightarrow \,\, \,\,\)

\(\displaystyle -\frac{1}{3}x^2+5x+y+\frac{5}{6} = 0\)

\( \displaystyle -\frac{1}{3}x^2+5x+y+\frac{5}{6} = 0\)

We have a quadratic equation in x

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,-\frac{1}{3}x^2+5x+y+\frac{5}{6}=0\)

By solving this quadratic equation on x, we obtain

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

and putting in the coefficients \(a = -\frac{1}{3}\), \(b = 5\) and \(c = y+\frac{5}{6}\)

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x = \frac{-\left( 5 \right) \pm \sqrt{\left( 5 \right)^2 - 4\left( -\frac{1}{3} \right)\left( y+\frac{5}{6} \right)}}{2\left( -\frac{1}{3} \right)}\)

from which we obtain

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2}, \,\,x=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2}\)

तो फिर, समाधान हैं:

\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]

एक-से-एक स्थिति

ऊपर दिखाए गए कार्य के आधार पर, यह निष्कर्ष निकाला जा सकता है कि दिया गया फ़ंक्शन वन-टू-वन नहीं है, क्योंकि यह क्षैतिज रेखा परीक्षण पास नहीं करता है, उदाहरण के लिए लाइन \(y = 0\) एक क्षैतिज रेखा है जो दिए गए फ़ंक्शन को पार करती है एक से ज्यादा बार।

ग्राफिक रूप से, स्थिति को इस प्रकार दर्शाया गया है:

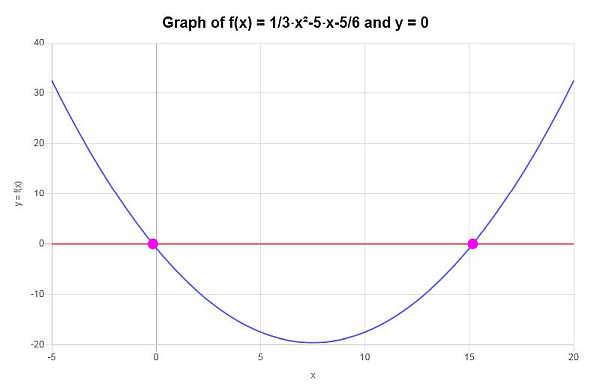
अधिक दिलचस्प बीजगणित कैलकुलेटर

1-टू-1 फ़ंक्शंस की अवधारणा को आम तौर पर हल्के में लिया जाता है, लेकिन मैं कहूंगा कि यह बहुत महत्वपूर्ण है। ऐसा इसलिए है क्योंकि वन-टू-वन की अवधारणा मोनोटोन फ़ंक्शन (बढ़ते या घटते फ़ंक्शन) के विचार से मजबूती से जुड़ी हुई है, ठीक उसी तरह जैसे कि यह बारीकी से संबंधित है व्युत्क्रम फलन की गणना और इसका ग्राफ.

फिर भी, कई बार पेड़ों के पार जंगल में जाना कठिन होता है, क्योंकि सबसे महत्वपूर्ण बीजगणित और कैलकुलस अवधारणाओं का एक-दूसरे के साथ गहरा संबंध होता है। कार्य विश्लेषण यह उन चीजों में से एक है जो आप हर समय करेंगे, इसलिए इसमें अच्छा बनने के लिए कौशल हासिल करना एक अच्छी बात है।