इस व्युत्क्रम फ़ंक्शन कैलकुलेटर पर अधिक जानकारी

यह कैलकुलेटर आपको सभी चरणों को दिखाते हुए किसी दिए गए फ़ंक्शन का व्युत्क्रम खोजने की अनुमति देगा, यह मानते हुए कि व्युत्क्रम मौजूद है। कैलकुलेटर फ़ंक्शन की जांच करेगा एक समीकरण हल करें फ़ंक्शन की परिभाषा से संबंधित है, और यह यह आकलन करने का प्रयास करेगा कि कोई व्युत्क्रम मौजूद है या नहीं।

उदाहरण के लिए, आप 'f(x) = 3x - 2' जैसा एक रैखिक फ़ंक्शन प्रदान कर सकते हैं, जो एक साधारण मामला होगा, या उदाहरण के लिए आप इसे कुछ कठिन चीज़ के साथ एक पायदान ऊपर ले जा सकते हैं, जैसे तर्कसंगत फ़ंक्शन के साथ 'y = (x-1)/(x-3)'।

एक बार जब आप एक वैध फ़ंक्शन प्रदान करते हैं, तो कृपया "गणना करें" बटन पर क्लिक करें ताकि प्रक्रिया के सभी चरण आपको दिखाए जा सकें, अंतिम उत्तर के रूप में व्युत्क्रम फ़ंक्शन के साथ, यदि कोई व्युत्क्रम मौजूद है, या स्पष्टीकरण के साथ कि कोई समाधान नहीं मिल सका और क्यों।

इसकी गारंटी नहीं है कि आपको सभी उलटे फ़ंक्शन मिलेंगे। एक के लिए, सभी कार्यों में व्युत्क्रम नहीं होता है, और दूसरे (जैसा कि हम अगले भाग में देखेंगे), व्युत्क्रम खोजने की प्रक्रिया में शामिल है एक्स के लिए हल करना एक समीकरण के लिए, और जैसा कि हम जानते हैं, कुछ समीकरणों को हल करना बहुत कठिन या असंभव हो सकता है।

तो फिर, यदि व्युत्क्रम मौजूद है, तो सरल कार्य उनके व्युत्क्रम को खोजने के लिए उत्तरदायी होने की अधिक संभावना रखते हैं।

आप किसी फ़ंक्शन के व्युत्क्रम को कैसे परिभाषित करते हैं?

आम आदमी के शब्दों में, किसी फ़ंक्शन का व्युत्क्रम वह फ़ंक्शन होता है जो मूल फ़ंक्शन के विपरीत कार्य करता है। तो, किसी फ़ंक्शन के बारे में y = f(x) के संदर्भ में सोचें, और फिर आप x से y तक जाते समय इसके बारे में सोच सकते हैं। आप फ़ंक्शन को x के साथ फ़ीड करते हैं, और फ़ंक्शन आपको एक विशिष्ट y देता है।

उलटा फ़ंक्शन y से शुरू होता है, और x पर वापस जाने का रास्ता ढूंढता है, इस तरह से कि x वही है जो मूल फ़ंक्शन के माध्यम से y तक ले जाता है। अब, औपचारिक परिभाषा के माध्यम से किया जाता है कार्य संरचना . फ़ंक्शन \(f\) के लिए, हम कहते हैं कि \(g\) \(f\) का व्युत्क्रम फ़ंक्शन है यदि

\[ f(g(x)) = x \]

और

\[ g(f(x)) = x \]

एक निश्चित सेट में सभी x के लिए। इसमें और भी बहुत कुछ है, लेकिन हम इसे सहज स्तर पर छोड़ देंगे (सख्ती से कहें तो, एक फ़ंक्शन को उलटा होने के लिए इंजेक्शन और विशेषण की आवश्यकता होती है, और कुछ अन्य तकनीकी चीजें जिन पर विचार किया जा रहा है, जैसे कि इसे प्रतिबंधित करना डोमेन और सीमा , वगैरह।)

आमतौर पर, हम \(f\) के व्युत्क्रम को \(f^{-1}\) कहते हैं, इसलिए व्युत्क्रम को परिभाषित करने वाला सूत्र आम तौर पर इस प्रकार लिखा जाता है:

\[ f(f^{-1}(x)) = x \]

व्युत्क्रम फलन ज्ञात करने के चरण क्या हैं?

यदि आपको कैलकुलस और डेरिवेटिव का उपयोग करना था (लेकिन ध्यान दें कि आपको इसकी आवश्यकता नहीं है संजात व्युत्क्रम की गणना करने के लिए), आप फ़ंक्शन का व्युत्पन्न पा सकते हैं, और यह सुनिश्चित कर सकते हैं कि व्युत्पन्न हमेशा सकारात्मक या नकारात्मक हो, यह सुनिश्चित करने के लिए कि फ़ंक्शन इंजेक्टिव है, और इसलिए, उलटा है।

लेकिन आमतौर पर, की पद्धति एक्स के लिए हल करना बुनियादी बीजगणित के विद्यार्थियों के लिए यह बहुत अधिक स्वादिष्ट है।

व्युत्क्रम फलन ज्ञात करने का नियम

वास्तव में y = f(x) से शुरू करने और फिर x के लिए हल करने के अलावा व्युत्क्रम फ़ंक्शन की गणना करने के लिए कोई अन्य नियम नहीं हैं। ऐसा नियम बहुत व्यापक लगता है, क्योंकि यह है। एक नियम से अधिक, यह प्रक्रिया शुरू करने की एक सामान्य पद्धति है।

अंततः व्युत्क्रम की गणना समीकरण को हल करने में आपकी सफलता और यह सुनिश्चित करने पर निर्भर करेगी कि समाधान अद्वितीय है। यह फ़ंक्शन के ग्राफ़ का पहले से आकलन करने में मदद करता है, ताकि जब स्पष्ट रूप से कोई न हो तो व्युत्क्रम की तलाश न की जाए।

ग्राफ़ में क्या देखना है? किसी फ़ंक्शन को उलटा होने के लिए एक निश्चित उपडोमेन पर मोनोटोन (बढ़ना या घटना) होना आवश्यक है। जैसा कि कहा जा रहा है, हम एक छोटे सेट में व्युत्क्रम खोजने के लिए किसी फ़ंक्शन के डोमेन को आसानी से एक छोटे उपडोमेन तक सीमित कर सकते हैं, यह हमेशा एक संभावना है।

हम निश्चित रूप से कैसे जान सकते हैं कि फलन का व्युत्क्रम है?

औपचारिक रूप से, यह सुनिश्चित करने का एकमात्र तरीका है कि किसी फ़ंक्शन का व्युत्क्रम है, आपको यह सुनिश्चित करना होगा कि फ़ंक्शन इंजेक्टिव (1-टू-1) है। इसका मूल्यांकन या तो इसके व्युत्पन्न (यदि यह मौजूद है) की गणना करके और यह सुनिश्चित करके किया जाता है कि यह हर जगह सकारात्मक और नकारात्मक है, या मैन्युअल रूप से यह सुनिश्चित करके कि जब हम y = f(x) से शुरू करते हैं और x के लिए हल करते हैं, तो हमें हमेशा एक अद्वितीय मिलता है समाधान।

इसे क्षैतिज रेखा परीक्षण का उपयोग करके ग्राफ़िक रूप से भी देखा जा सकता है: आप एक मनमाना क्षैतिज रेखा खींचते हैं, और फ़ंक्शन f(x) क्षैतिज रेखा परीक्षण पास करता है यदि खींची गई कोई क्षैतिज रेखा फ़ंक्शन के ग्राफ़ को अधिकतम एक बार पार करती है।

उदाहरण: व्युत्क्रम फलन ढूँढना

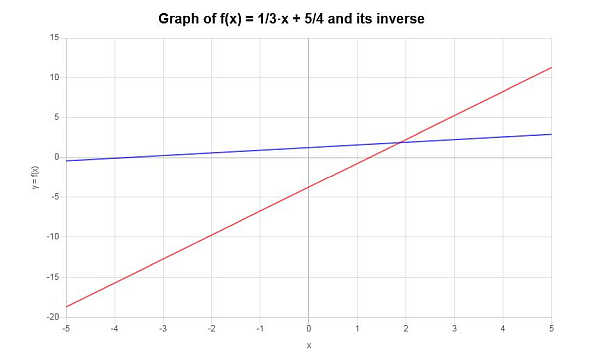
निम्नलिखित फ़ंक्शन का व्युत्क्रम ज्ञात कीजिए: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)

समाधान:

हमारे पास निम्नलिखित कार्य हैं:

\[f(x) = \frac{1}{3} x + \frac{5}{4}\]

फिर, दिए गए फ़ंक्शन का व्युत्क्रम खोजने के लिए, हमें \(x\) को हल करना होगा और यह निर्धारित करना होगा कि कोई समाधान है या नहीं। प्रारंभिक समीकरण है:

\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]

चरण 0: इस मामले में, हमें पहले दिए गए रैखिक समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

रैखिक समीकरण को हल करना

बाएं हाथ की तरफ \(x\) और \(y\) और दाहिने हाथ की तरफ स्थिर

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(-\frac{1}{3}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=3y-\frac{15}{4}\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(y\) को हल करने पर \(x=3y-\frac{15}{4}\) प्राप्त होता है।

इसलिए, और चूँकि \(x\) को हल करते समय हमें एक समाधान मिलता है और यह केवल एक ही समाधान है, हमने व्युत्क्रम पाया है।

व्युत्क्रम फलन

ऊपर दिखाए गए कार्य के आधार पर, यह निष्कर्ष निकाला जा सकता है कि उलटा कार्य है:

\[f^{-1}(x) = 3x-\frac{15}{4}\]

व्युत्क्रम फलन को ग्राफ़िक रूप से इस प्रकार दर्शाया जा सकता है:

उदाहरण: अधिक उलटे उदाहरण

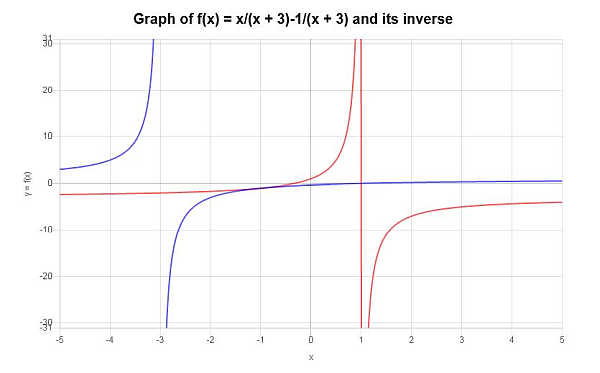
इसके व्युत्क्रम फलन की गणना करें: \(y = \frac{x-1}{x+3}\)

समाधान:

दिए गए फ़ंक्शन का व्युत्क्रम खोजने के लिए, हम \(x\) को हल करते हैं और निर्धारित करते हैं कि कोई समाधान है या नहीं। प्रारंभिक समीकरण है:

\[y=\frac{x-1}{x+3}\]

निम्नलिखित प्राप्त होता है:

सहायक अंश समीकरण

हमें अंश को शून्य के बराबर सेट करना होगा और समाधान ढूंढना होगा। फिर, वे मूल जो हर को शून्य के बराबर नहीं बनाते, तर्कसंगत समीकरण के समाधान होंगे

उपरोक्त बहुपद समीकरण में बीजगणितीय हेरफेर का उपयोग करके, निम्नलिखित प्राप्त किया जाता है:

\[x = -\frac{3y+1}{y-1} \]

सहायक हर समीकरण

हम हर के मूल ज्ञात करते हैं: \(x+3=0\)

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने पर \(x=-3\) प्राप्त होता है।

तर्कसंगत समीकरण के समाधानों को एक साथ रखना

फिर, यह जांच कर कि हमारे पास हर का शून्य नहीं है, हम समीकरण \(\displaystyle y=\frac{x-1}{x+3}\) के लिए निर्धारित निम्नलिखित समाधान पाते हैं

\[x = -\frac{3y+1}{y-1} \]

चूँकि जब हम \(x\) को हल करते हैं तो हमें एक और केवल एक ही समाधान मिलता है, हम यह निष्कर्ष निकालते हैं कि हमारे पास एक व्युत्क्रम फलन है।

व्युत्क्रम फलन ढूँढना

ऊपर दिखाए गए कार्य के आधार पर, यह निष्कर्ष निकाला जा सकता है कि उलटा कार्य है:

\[f^{-1}(x) = -\frac{3x+1}{x-1}\]

पाए गए व्युत्क्रम फ़ंक्शन को ग्राफ़िक रूप से निम्नानुसार दर्शाया जा सकता है:

उदाहरण: सभी फलनों का व्युत्क्रम नहीं होता

क्या निम्नलिखित फ़ंक्शन का व्युत्क्रम है: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \)?

समाधान: उसका अवलोकन करो

\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]

जो इंगित करता है कि दो समाधान हैं, और फिर, इस मामले में कोई व्युत्क्रम नहीं है।

अधिक फ़ंक्शन कैलकुलेटर

गणित में फ़ंक्शंस एक महत्वपूर्ण वस्तु हैं, विशेष रूप से कैलकुलस और बीजगणित में, जहां फ़ंक्शंस के माध्यम से चर के बीच बहुत सारे संबंध स्थापित किए जाते हैं।

ऐसी बहुत सी चीज़ें हैं जो आप फ़ंक्शन के साथ कर सकते हैं: आप कर सकते हैं उन्हें सरल बनाएं , तुम कर सकते हो किसी फ़ंक्शन को अलग करना , आप उन्हें संचालित कर सकते हैं, किसी अन्य फ़ंक्शन के साथ कंपोजिट ढूंढ सकते हैं, और सूची चालू हो जाती है।

कई बार, भले ही आप कार्यों का स्पष्ट रूप से उल्लेख कर रहे हों, आपके पास पूरी प्रक्रिया के अंतर्निहित कार्य होते हैं। तो वे वहाँ हैं, भले ही कभी-कभी आप इसे नहीं जानते हों। एक बड़ी बात यह है कि बहुत जटिल मामलों में भी, आप हमेशा ऐसा कर सकते हैं एक फ़ंक्शन ग्राफ इसके व्यवहार का अंदाजा लगाने के लिए, ताकि कम से कम यह जान सकें कि फ़ंक्शन क्या करता है (ऊपर जाता है, नीचे जाता है, आदि)।