More About this Dot Product Calculator

This calculator will allow you to calculate the dot product of two vectors, showing all the steps. All you need to do is to type the vectors and click on 'Calculate'.

Dot product have a LOT of applications in Linear Algebra, for computing projections and assessing perpendicularity of vectors.

Indeed, geometrically speaking a dot product that is equal to zero implies that the two vectors are perpendicular.

The Dot Product Formula

so, how do you calculate dot product? The dot product is an operation conducted for two vectors \(x\) and \(y\), and the result of the operation is a scalar. The formula for the dot product is shown below:

\[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i \]

The dot product \(\langle x,y \rangle\) is known by different names, and it is also called, inner product or scalar product . Essentially, the dot product is matrix product if we consider \(x \in \mathbb{R}^n\) and \(y \in \mathbb{R}^n\), then the dot product is defined as:

\[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i = x^t \cdot y \]

This formula is easy to remember unlike the case of the cross product. It is easy to calculate dot product by hand, as in the case of the dot product you multiply the corresponding component and then you add them up.

Dot Product Applications

Some uses of the dot product are super neat and practical: The dot product calculator and the angle. Indeed, the dot or inner product also has a strong geometric motivation. Certainly, an alternative expression for it is

\[ \langle x, y \rangle = \|x\| \|y\| \cos \theta \]

where \(\|x\|\) is the norm (length) of \(x\), \(\|y\|\) is the norm (length) of \(y\), and \(\theta\) is the angle between \(x\) and \(y\).

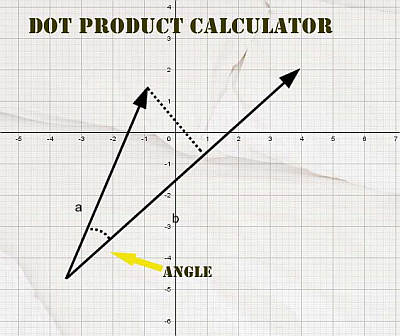
Dot Product with Angle Calculation

A direct consequence of the definition of dot product is that you can use it to compute the angle between two vectors, using the following formula:

\[\cos \theta = \displaystyle \frac{ \langle x, y \rangle}{\|x\| \|y\| } \]

and if we solved for \(\theta\):

\[ \theta = \arccos\left( \displaystyle \frac{ \langle x, y \rangle}{\|x\| \|y\| } \right) \]

The dot product and the cross product

A related operation for two vectors is the cross product , although it has a different now since its output is a vector and not a scalar.

More Algebra Calculators

You can browse around and see more algebra solvers in our algebra calculators and solvers section.

Calculators of dot product and cross product, among many others have a strong degree of applicability in the Linear Algebra and Geometry.

Although some computer systems can show you the answers, our calculators will show you the steps so you understand where things are coming from.