حل المعادلات الجذرية

يسمح لك حل المعادلات الجذرية هذا بالتعامل مع المعادلات الجذرية التي تقدمها, من خلال معالجتها جبريًا مع عرض جميع خطوات العملية لك.

سيقبل هذا الحل أي معادلة صالحة تتضمن جذورًا, مثل شيء بسيط جدًا مثل 'sqrt(x) = 1', أو شيء يمكن أن يكون حله أصعب كثيرًا مثل 'sqrt(x+3) = x^2 - 1'.

بمجرد تقديم معادلة جذرية صالحة, تكون قد انتهيت بشكل أساسي وكل ما تبقى عليك فعله هو النقر فوق "حل" للحصول على جميع خطوات العملية الموضحة.

حل المعادلة الجذرية القوية يعتمد على الفعال التلاعب الجبري بالتعبير , من أجل التخلص بشكل أساسي من الجزء الجذري.

ما هي المعادلة الجذرية

المعادلة الجذرية, بعبارات بسيطة للغاية, هي نوع من معادلة الرياضيات حيث يكون المجهول (عادةً x) داخل الجذر. على سبيل المثال

\[\displaystyle \sqrt x = x^2 \]

هي معادلة جذرية, بسبب المصطلح \( \sqrt x\), ولكن المعادلة

\[\displaystyle 2 x = x^2 \]

على سبيل المثال, ليست معادلة جذرية, لأننا لا نستطيع x من الداخل لجذر في أي مكان في المعادلة.

كيفية حل المعادلات الجذرية

حل المعادلات الجذرية ليس بالأمر الصعب إذا اتبعت الخطوات التالية:

في بعض الأحيان, بغض النظر عن التجميع والتبسيط المناسب, لن يكون من الممكن إزالة الجذور تمامًا, أو سيؤدي ذلك إلى معادلة أكثر تعقيدًا.

تبسيط المعادلات الجذرية

كما ذكرنا أعلاه, فإن الحساب الناجح للمعادلات التي تتضمن جذورًا يعتمد بشدة على القدرة على ذلك تيبسيط الهاور . لكن في بعض الأحيان لن يكون ذلك كافيًا, لأن تبسيط جميع الجذور الموجودة لن يجعلها تختفي. الطريقة الأكثر شيوعًا هي تقليل الجذور ثم تطبيق المربع (قوة 2) لإلغاء الجذر.

لكن التربيع للتخلص من الجذر هو حد سيف مزدوج, لأنه من خلال التربيع يمكن أن تختفي أي إشارة ذات صلة. هذا هو ما عند "إزالة" الحلول الجذرية وإيجاد حلول لمعادلة مساعدة, يجب علينا التحقق مرة أخرى من أن الحلول المساعدة هي أيضًا حلول للمعادلة الأصلية. في كثير من الأحيان لا يكونون كذلك.

هناك طريقة أخرى لرؤية عملية إزالة الجذر وهي استخدام الاستبدال المناسب. على سبيل المثال, بالنسبة للمعادلة الجذرية:

\[\displaystyle \sqrt x = x \]

قد ترغب في تعيين \(u = \sqrt x\), إذن \(u^2 = (\sqrt x)^2 = x\), وبالتالي تتحول المعادلة الأصلية إلى المعادلة المساعدة التالية:

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

وهي معادلة متعددة الحدود يمكننا حلها. إذن, استخدام الاستبدال يؤدي إلى معادلة لا نعرف كيفية حلها حل معادلة متعددة الحدود والتي نعرف من يجب حلها.

لماذا نهتم بالمعادلات الجذرية؟

المعادلات الجذرية هي مظاهر شائعة في الجبر وحساب التفاضل والتكامل, لأنها أساس نمذجة العديد من الظواهر المختلفة.

تعتبر الوظائف الجذرية مثيرة للاهتمام من حيث خصائصها ونوع النمو البطيء مع اقتراب x من اللانهاية.

مثال: حل المعادلات التي تتضمن جذرية

حل ما يلي: \(\sqrt{x} = 2x\)

حل:

يتم تزويدنا بالمعادلة التالية. نحتاج إلى حل هذه المعادلة التي تحتوي على متغير واحد فقط, وهو \(x\), لذا فإن الهدف هو حل \(x\):

\[\sqrt{x}=x^2\]

لاحظ أن درجة متعدد الحدود المعطاة هي \(\displaystyle deg(p) = 4\), معامله الرائد هو \(\displaystyle a_{4} = -1\)ومعامله الثابت هو \(\displaystyle a_0 = 0\).

محاولة الجذور العقلانية

الممرى الهاون : بما أن الحد الأول بمعامل غير الصفر في \(p(x)\) هو \(x\), يمكننا تحليل هذا الحد للحصول على

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

لكن المصطلح بين قوسين له درجة أعلى من 2 , لذلك لا توجد صيغة أولية لتوضيح ذلك.نحن بحاجة إلى اختبار جذور عقلانية محتملة.

المهمة التالية هي العثور على الأعداد الصحيحة التي تقسم المعامل الرئيسي \(a_{3}\) والمعامل الثابت \(a_0\), والتي سيتم استخدامها لبناء مرشحينا ليكونوا أصفارًا في المعادلة كثيرة الحدود.

لذلك, بقسمة كل مقسم للمعامل الثابت \(a_0 = 1\) على كل مقسم للمعامل الرئيسي \(a_{3} = -1\), نجد القائمة التالية من المرشحين لتكون جذور:

\[\pm \frac{ 1}{ 1}\]

الآن , يجب اختبار جميع المرشحين لمعرفة ما إذا كانوا حلًا.يتم الحصول على ما يلي من اختبار كل مرشح:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

آمتوم مقتد دداود : بما أنه ليس لدينا جذور كافية بين المرشحين العقلانيين, فسنقسم \(\displaystyle -x^3+1\) على حاصل ضرب العوامل المشتقة من الجذور المنطقية, وهو \(\displaystyle \left(x-1\right) \).

الظهر 1: الحد الرئيسي لتوزيع الأرباح \(\displaystyle p(x) = -x^3+1\) هو \(\displaystyle -x^3\), في حين أن الحد الرئيسي للمقسوم عليه \(\displaystyle s(x) = x-1\) يساوي \(\displaystyle x\).

إذن, الحد الذي نحتاج إلى ضرب \(x\) للوصول إلى الحد الرئيسي للمقسّم هو \(\displaystyle \frac{ -x^3}{ x} = -x^2\), لذلك نضيف هذا الحد إلى خارج القسمة. أيضًا, نضرب هذا في المقسوم عليه لنحصل على \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), والذي نحتاج إلى طرحه إلى المقسوم:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

ال alخطoة 2: الآن, الحد الرئيسي للباقي الحالي \(\displaystyle -x^2+1\) هو \(\displaystyle -x^2\), ونحن نعلم أن الحد الرئيسي للمقسوم عليه هو \(\displaystyle x\).

إذن, الحد الذي نحتاج إلى ضرب \(x\) للوصول إلى الحد الرئيسي للباقي الحالي هو \(\displaystyle \frac{ -x^2}{ x} = -x\), لذلك نضيف هذا الحد إلى خارج القسمة. أيضًا, نضرب هذا في المقسوم عليه لنحصل على \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), والذي نحتاج إلى طرحه للتذكير الحالي:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

الله 3: الآن, الحد الرئيسي للباقي الحالي \(\displaystyle -x+1\) هو \(\displaystyle -x\), ونحن نعلم أن الحد الرئيسي للمقسوم عليه هو \(\displaystyle x\).

إذن, الحد الذي نحتاج إلى ضرب \(x\) للوصول إلى الحد الرئيسي للباقي الحالي هو \(\displaystyle \frac{ -x}{ x} = -1\), لذلك نضيف هذا الحد إلى خارج القسمة. أيضًا, نضرب هذا في المقسوم عليه لنحصل على \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), والذي نحتاج إلى طرحه للتذكير الحالي:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

ولذلك, فإن الحاصل هو \(\displaystyle q(x) = -x^2-x-1\), والباقي هو \(\displaystyle r(x) = 0\).

لذلك بعد الانقسام , تقدمنا في العوامل مع

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

لكن الآن, بما أن حاصل القسمة \(\displaystyle -x^2-x-1\) هو تربيعي, فيمكننا العثور على جذوره لمعرفة ما إذا كان بإمكاننا تحليله في المجال الحقيقي.

نحتاج إلى حل المعادلة التربيعية التالية \(\displaystyle -x^2-x-1=0\).

باستخدام الصيغة التربيعية

للمعادلة التربيعية للنموذج \(a x^2 + bx + c = 0\), يتم حساب الجذور باستخدام الصيغة التالية:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

في هذه الحالة , لدينا أن المعادلة التي نحتاج إلى حلها هي \(\displaystyle -x^2-x-1 = 0\), مما يعني أن المعاملات المقابلة هي:

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

بما أننا في هذه الحالة حصلنا على المميز \(\Delta = \displaystyle -3 < 0\), وهو سلبي, فإننا نعلم أن المعادلة المعطاة لها جذرين معقدين مترافقين مختلفين.

الآن , توصيل هذه القيم في صيغة الجذور التي نحصل عليها:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

إذن , نجد ذلك:

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

لذلك بعد إيجاد جذور الجزء التربيعي الأخير, نجد جذرين معقدين, لذلك لا يمكننا تحليل المصطلح \(-x^2-x-1\) في المجال الحقيقي, لذلك ننهي العملية بـ \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).

ولذلك, فإن حل \(x\) للمعادلة كثيرة الحدود المعطاة يؤدي إلى الحلول \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), باستخدام طرق التحليل.

التحقق من الحلول المساعدة

يُظهر اختبار هذه الحلول من معادلة متعددة الحدود المساعدة أنه ليست كل الحلول المرشحة هي في الواقع حل للمعادلة الأصلية. الحلول الفعلية الوحيدة للمعادلة الأصلية هي:

\[x_1=0 \]
\[x_2=1 \]

ولذلك, فإن حل \(x\) للمعادلة المعطاة يؤدي إلى الحلول \(x=0,\,\,x=1\).

بيانياً

فيما يلي تمثيل رسومي للحلول التي تم الحصول عليها:

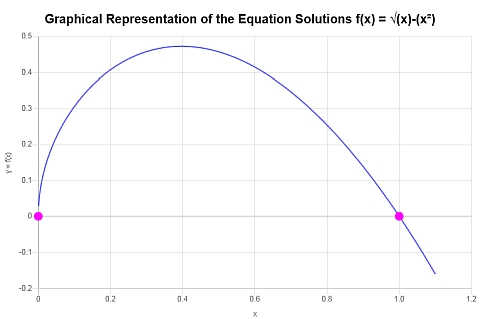
الذي يختتم الحساب.

أدوات حل المعادلات المفيدة الأخرى

عند حل المعادلات الجذرية, على عكس الحالة عندما تحتاج إلى ذلك حل المعادلات الخطية أو عندما تحتاج إلى ذلك حل معادلة تربيعية , تندرج ضمن فئة تلك المعادلات التي تتطلب معالجة جبرية ذكية جدًا لحل قيمة x.

بمعنى آخر, لن يكون لديك عبارة "افعلها بهذه الطريقة وسوف تنجح دائمًا". يعتمد نوع التلاعب الذي تقوم به على بنية المعادلة, ويمكن أن يختلف بشكل كبير من حالة إلى أخرى.

تيبسيه يعد الأول دائمًا ممارسة جيدة, لأنك ستقلل من الحدود التي قد تشوش البنية العامة للمعادلة.