المحللين الجبر

حاسبة الدالة العكسية

تعليمات: استخدم هذه الآلة الحاسبة للعثور على الدالة العكسية للدالة التي تقدمها, مع عرض جميع الخطوات. يرجى كتابة تعبير الدالة الذي تريد العثور على معكوس له في المربع أدناه.

كيف يمكنك تحديد معكوس الوظيفة؟

في مصطلحات الشخص العادي, معكوس الوظيفة هو الوظيفة التي تفعل عكس ما تفعله الوظيفة الأصلية. لذا, فكر في دالة بدلالة y = f(x), ومن ثم يمكنك التفكير فيها أثناء الانتقال من x إلى y. تقوم بتغذية الدالة بـ x, وتمنحك الدالة y محددًا.

تبدأ الدالة العكسية بـ y, وتجد طريق العودة إلى x, بحيث تكون x هي نفسها التي أدت إلى y من خلال الدالة الأصلية. الآن, يتم التعريف الرسمي عبر تكوين الوظيفة . بالنسبة للدالة \(f\), نقول أن \(g\) هي الدالة العكسية للدالة \(f\) إذا

\[ f(g(x)) = x \]

\[ g(f(x)) = x \]

لجميع x في مجموعة معينة. هناك ما هو أكثر من ذلك, ولكننا سنترك الأمر على المستوى البديهي (بالمعنى الدقيق للكلمة, يجب أن تكون الوظيفة حقنية وقاطعة حتى تكون قابلة للعكس, وبعض الجوانب الفنية الأخرى التي يجب أخذها في الاعتبار, مثل تقييد المجال والمدى , إلخ.)

عادة, نطلق \(f^{-1}\) على معكوس \(f\), لذلك تتم كتابة الصيغة التي تحدد العكس عادةً على النحو التالي:

\[ f(f^{-1}(x)) = x \]

ما هي خطوات إيجاد الدالة العكسية؟

                                    
                                                الخطوة 1:
                                            
                                            ابدأ بالمعادلة التي تحدد الدالة, أي أنك تبدأ بـ y = f(x)
                                        
                                                الخطوة 2:
                                            
                                            ثم تستخدم المعالجة الجبرية لحل مشكلة x. اعتمادًا على مدى تعقيد f(x), قد تجد أن حل x أسهل أو أصعب.
                                        
                                                الخطوه 3:
                                            
                                            في بعض الظروف, لن تتمكن ببساطة من إيجاد قيمة x للدوال غير الخطية المعقدة f(x)
                                        
                                                الخطوة 4:
                                            
                                            إذا كنت قادرًا على حل قيمة x, فيجب أن تكون قادرًا على كتابة x = g(y)
                                        
                                                الخطوة 5:
                                            
                                            أنت بحاجة إلى تقييم ما إذا كان الحل الذي تم العثور عليه فريدًا أم لا. هذا يمكن حله لـ x بشكل فريد. بمعنى آخر, هل وجدت حلًا واحدًا فقط عند حل قيمة x؟ إذا كانت الإجابة بنعم, فهذا يعني أن لديك دالة عكسية, وإلا فلا يوجد معكوس
                                        
                                                الخطوة 6:
                                            
                                            إذا وجدت المعكوس عن طريق حل x = g(y), فما عليك سوى تغيير اسم المتغير وكتابة f
                                            
                                                -1
                                            
                                            (x) = g(x), مما يجعل التركيز في g(x) هو المعكوس الفعلي

إذا كنت ستستخدم حساب التفاضل والتكامل والمشتقات (ولكن لاحظ أنك لا تحتاج إلى ذلك المشتقات لحساب المعكوس), يمكنك العثور على مشتقة الدالة, والتأكد من أن المشتقة دائمًا موجبة أو سالبة, للتأكد من أن الدالة قابلة للحقن, وبالتالي قابلة للعكس.

لكن عادة ما تكون منهجية حل ل x هو أكثر قبولا لطلاب الجبر الأساسي.

قاعدة إيجاد الدوال العكسية

في الواقع لا توجد قواعد أخرى لحساب الدالة العكسية بخلاف البدء بـ y = f(x) ثم حل x. تبدو قاعدة كهذه واسعة جدًا, لأنها كذلك بالفعل. إنها أكثر من مجرد قاعدة, إنها منهجية عامة للبدء في هذه العملية.

في النهاية, حساب المعكوس سيعتمد على نجاحك في حل المعادلة, والتأكد من أن الحل فريد. من المفيد تقييم الرسم البياني للدالة مسبقًا, حتى لا تبحث عن معكوس عندما لا يكون هناك أي معكوس.

ما الذي يجب أن ننظر إليه في الرسم البياني؟ يجب أن تكون الوظيفة رتيبة (زيادة أو نقصان) في مجال فرعي معين حتى تكون قابلة للعكس. مع ما قيل, يمكننا بسهولة تقييد مجال الدالة إلى مجال فرعي أصغر للعثور على المعكوس في مجموعة أصغر, وهذا هو الاحتمال دائمًا.

كيف نعرف على وجه اليقين أن الدالة لها معكوس؟

رسميًا, الطريقة الوحيدة للتأكد من أن الدالة لها معكوس, تحتاج إلى التأكد من أن الدالة حقنية (1 إلى 1). يتم تقييم ذلك إما عن طريق حساب مشتقته (إذا كانت موجودة) والتأكد من أنها موجبة وسالبة في كل مكان, أو عن طريق التأكد يدويًا من أنه عندما نبدأ بـ y = f(x) ونحلها من أجل x, فإننا نحصل دائمًا على قيمة فريدة حل.

يمكن رؤية ذلك أيضًا بيانيًا, باستخدام اختبار الخط الأفقي: ترسم خطًا أفقيًا عشوائيًا, وتجتاز الدالة f(x) اختبار الخط الأفقي إذا كان أي خط أفقي مرسوم يتقاطع مع الرسم البياني للدالة مرة واحدة على الأكثر.

مثال: إيجاد الدالة العكسية

أوجد معكوس الدالة التالية: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)

حل:

لدينا الوظيفة التالية:

\[f(x) = \frac{1}{3} x + \frac{5}{4}\]

ثم, من أجل العثور على معكوس الدالة المعطاة, نحتاج إلى حل \(x\) وتحديد ما إذا كان هناك حل أم لا. معادلة البداية هي:

\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]

الخطوة 0: في هذه الحالة, نحتاج أولاً إلى تبسيط المعادلة الخطية المعطاة, وللقيام بذلك, نقوم بخطوات التبسيط التالية:

\( \displaystyle y-\left(\frac{1}{3}x+\frac{5}{4}\right) = 0\)

The multiplication by -1 gets distributed as follows: \(-\left(\frac{5}{4}+\frac{1}{3}x\right) = -\frac{5}{4}-\frac{1}{3}x\)

\( \displaystyle \Rightarrow \,\, \,\,\)

\(\displaystyle y-\frac{5}{4}-\frac{1}{3}x = 0\)

حل المعادلة الخطية

وضع \(x\) على الجانب الأيسر و \(y\) والثابت على الجانب الأيمن الذي نحصل عليه

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

الآن , حل \(x\), من خلال تقسيم جانبي المعادلة بواسطة \(-\frac{1}{3}\), يتم الحصول على ما يلي

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

وتبسيط نحصل أخيرًا على ما يلي

\[\displaystyle x=3y-\frac{15}{4}\]

ولذلك, فإن حل \(y\) لمعادلة خطية معينة يؤدي إلى \(x=3y-\frac{15}{4}\).

ولذلك, وبما أنه عند حل \(x\) نجد حلاً وهو حل واحد فقط, فقد وجدنا العكس.

الدالة العكسية

بناءً على العمل الموضح أعلاه, يمكن استنتاج أن الدالة العكسية هي:

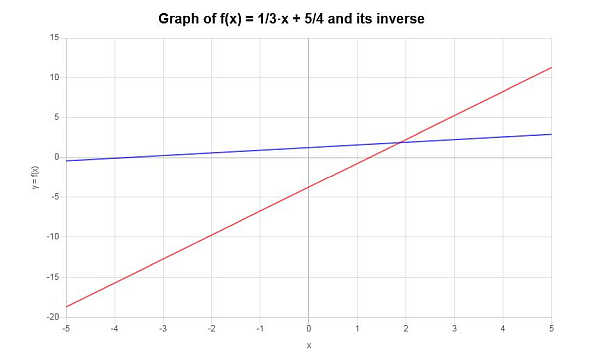
\[f^{-1}(x) = 3x-\frac{15}{4}\]

يمكن تمثيل الدالة العكسية بيانيا على النحو التالي:

مثال: المزيد من الأمثلة العكسية

حساب الدالة العكسية لـ: \(y = \frac{x-1}{x+3}\)

حل:

من أجل إيجاد معكوس الدالة المعطاة, نحل لـ \(x\) ونحدد ما إذا كان هناك حل أم لا. معادلة البداية هي:

\[y=\frac{x-1}{x+3}\]

ويتم الحصول على ما يلي:

\( \displaystyle y=\frac{x-1}{x+3}\)

Putting all the terms of the equation on one side

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,y-\frac{x}{x+3}+\frac{1}{x+3}=0\)

We reorganize the terms so to get a rational equation structure

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,\frac{\left(x+3\right)y-x+1}{x+3}=0\)

By simpliflying we find

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,\frac{xy-x+3y+1}{x+3}=0\)

معادلة البسط المساعدة

علينا أن نجعل البسط يساوي صفرًا ونوجد الحلول. إذن, تلك الجذور التي لا تجعل المقام يساوي صفرًا ستكون حلولاً للمعادلة النسبية

\( \displaystyle xy-x+3y+1=0\)

Keeping the term with \(x\) on one side and the rest of terms on the other side

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,\left(y-1\right)x = -3y-1\)

Dividing the equation by \(y-1\)

\( \displaystyle \,\,\)

\(\displaystyle \Rightarrow \,\,\,\,x = -\frac{3y}{y-1}-\frac{1}{y-1}\)

باستخدام المعالجة الجبرية للمعادلة متعددة الحدود المذكورة أعلاه, يتم الحصول على ما يلي:

\[x = -\frac{3y+1}{y-1} \]

معادلة المقام المساعد

نجد جذور المقام: \(x+3=0\)

ولذلك, فإن حل \(x\) لمعادلة خطية معينة يؤدي إلى \(x=-3\).

تجميع حلول المعادلة العقلانية

بعد ذلك, وبالتحقق من عدم وجود صفر للمقام, نجد أن مجموعة الحل التالية للمعادلة \(\displaystyle y=\frac{x-1}{x+3}\) هي

\[x = -\frac{3y+1}{y-1} \]

وبما أننا عندما نحل لـ \(x\) نجد حلًا واحدًا فقط, فإننا نستنتج أن لدينا دالة عكسية.

إيجاد الدالة العكسية

بناءً على العمل الموضح أعلاه, يمكن استنتاج أن الدالة العكسية هي:

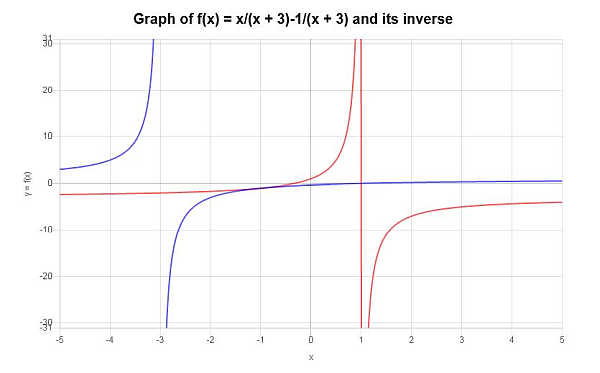
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]

يمكن تصوير الدالة العكسية التي تم العثور عليها بيانياً على النحو التالي:

مثال: ليست كل الدوال لها معكوس

هل للدالة التالية معكوس: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ؟

حل: لاحظ ان

\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]

مما يدل على أن هناك حلين, ومن ثم لا يوجد معكوس في هذه الحالة.