المجال والمدى
مجال الوظيفة هو مجموعة يتم فيها تعريف الوظيفة بشكل جيد. بشكل أكثر تحديدًا , دع \(f: D \rightarrow R\) تكون دالة , مما يعني أن \(f(a)\) محددة جيدًا لـ \(a \in D\). مجال الوظيفة \(f\) هو المجموعة \(D\).
رياضيا سوف تكتب \(dom(f) = D\).
نطاق الوظيفة , من ناحية أخرى , هو مجموعة من القيم التي يمكن الوصول إليها عبر الوظيفة.
بشكل أكثر تحديدًا , دع \(f: D \rightarrow R\) تكون دالة , النطاق هو مجموعة جميع القيم الممكنة \(b \in R\) التي يوجد لها \(a \in D\) مثل \(f(a) = b\).
غالبًا ما تتم كتابة نطاق الدالة كـ \(R(f)\) أو أيضًا باسم \(f(D)\) (والتي تُعرف أيضًا باسم مجموعة الصور \(D\) من خلال الوظيفة \(f\)).
من الأهمية بمكان معرفة مجال الوظيفة لأن ذلك يعطينا مجموعة آمنة من القيم التي يتم تحديد الوظيفة بشكل جيد على أساسها.
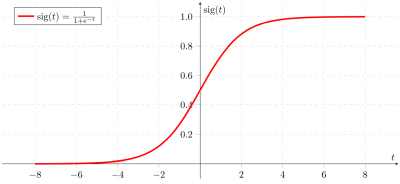
بعد ذلك , يعد النطاق مهمًا لأنه يخبرنا بالقيم التي تصل إليها الوظيفة. تفسير أكثر بيانية هو هذا: النقطة \(b\) تقع في نطاق \(f\) إذا كان الخط الأفقي \(y = b\) يتقاطع مع الرسم البياني للدالة \(f(x)\).
كيف تحسب المجال من الناحية العملية؟
إليك كيفية العثور على المجال والمدى :
بالنسبة للمجال , تحتاج أولاً إلى إيجاد النقاط التي لم يتم فيها تحديد الوظيفة. مصادر العمليات غير المعرفة هي القسمة على صفر أو الجذر التربيعي لأرقام سالبة.
لذلك , تحتاج إلى العثور على تلك النقاط (إن وجدت) حيث تحدث هذه العمليات غير المحددة. وسيكون المجال هو باقي النقاط , أي جميع النقاط باستثناء تلك التي تجدها والتي تسبب عمليات غير محددة.
كيف تحسب المدى من الناحية العملية؟
لنفترض أن \(y\) رقم وسنحل من أجل \(x\) المعادلة التالية \(f(x) = y\). تقع القيمة \(y\) في النطاق إذا كان من الممكن حل \(f(x) = y\) من أجل \(x\).
لذلك هذا أصعب قليلاً: تحتاج إلى معرفة ما إذا كنت بحاجة إلى تقييد \(y\) بأي طريقة بحيث يكون \(f(x) = y\) لديه حل لـ \(x\).
مثال 1
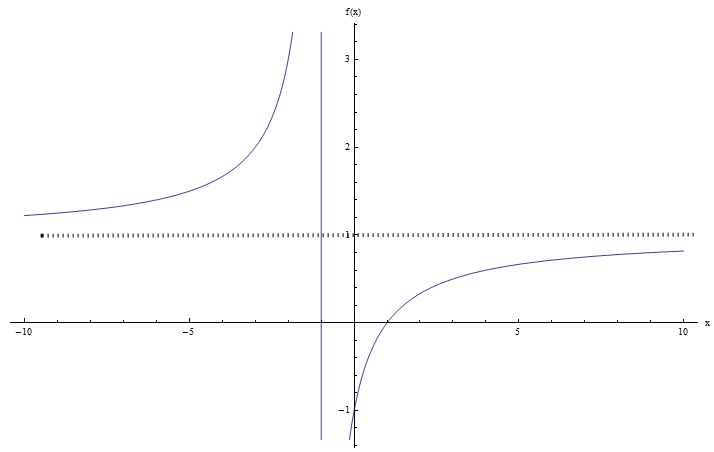
احسب مجال ومدى الدالة \(\displaystyle f(x) = \frac{x+1}{x-1}\).
إجابه:
أولاً , نحتاج إلى حساب المجال. نحن بحاجة إلى معرفة مكان تحديد الوظيفة بشكل جيد. عادة ما يكون من الأسهل البدء من حيث لم يتم تحديده بشكل جيد.
لذا في هذه الحالة , تبدو جميعها عمليات صحيحة , باستثناء أمر واحد: لا يمكن أن يكون المقام صفراً.
ملحوظة: تتمثل المفاتيح الرئيسية للعثور على المجال في تحديد النقاط التي توجد بها أقسام محتملة على الصفر , أو جذور تربيعية محتملة للقيم السالبة , وهي عمليات غير صالحة.
لذلك , يتم تحديد الوظيفة جيدًا باستثناء حالة \(x-1 = 0\) , والتي تحدث عند \(x = 1\). ومن ثم , نقول أن المجال هو السطر الحقيقي بالكامل باستثناء القيمة \(1\).
باستخدام تدوين الفاصل الزمني , نكتب \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).
الآن نحن بحاجة لحساب النطاق. عادةً , قد يكون الحصول على النطاق أكثر صعوبة من الحصول على النطاق , ولكن ها نحن ذا.
هناك العديد من الطرق للعثور على النطاق: قد يعتمد البعض على التمثيل الرسومي للدالة لتقديم مطالبة حول نطاق الدالة. يمكن أن ينجح هذا , لكنه ليس إجابة حقيقية , فقط حدس مثقف.
الطريقة الأخرى هي الطريقة الرياضية الرسمية: لنفترض أن \(y\) يكون رقمًا وسنحل من أجل \(x\) المعادلة التالية \(f(x) = y\). تقع القيمة \(y\) في النطاق إذا كان من الممكن حل \(f(x) = y\) من أجل \(x\).
في هذه الحالة لدينا:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-1} = y\] \[\Rightarrow \,\,\,x+1=y\left( x-1 \right)\] \[\Rightarrow \,\,\,x+1=yx-y\] \[\Rightarrow \,\,\,x-yx=-1-y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-y\] \[\Rightarrow \,\,\,x=\frac{y+1}{y-1}\]إذن , متى يتم تعريف \(x\) جيدًا؟ تقريبًا لجميع \(y\) , باستثناء الوقت \(y = 1\) , لأنه في هذه الحالة لدينا قسمة على \(0\). ومن ثم , فإن نطاق \(f\) في هذه الحالة هو الخط الحقيقي بالكامل , باستثناء 1.
باستخدام تدوين الفاصل الزمني , نكتب \(R(f) = (-\infty, 1) \cup (1, +\infty)\).
مثال 2
احسب مجال ومدى الدالة \(\displaystyle f(x) = \sqrt{x+1}\).
إجابه:
تذكر , للعثور على المجال , نحتاج إلى البحث عن النقاط التي قد تحدث فيها عمليات غير صالحة (القسمة على الصفر أو الجذور التربيعية للقيم السالبة. لا توجد أقسام في هذه الحالة , لكننا نحتاج إلى التأكد من أن \(x+1\ge 0\) بحيث لا توجد جذور تربيعية من القيم السالبة. إذن نحن بحاجة إلى \(x \ge -1\). باستخدام تدوين الفترة , نكتب \(dom(f) = [-1, +\infty)\).
.الآن بالنسبة إلى النطاق , نحتاج إلى إيجاد قيمة \(x\): \(\sqrt{x+1} = y\). الجذر التربيعي لشيء ما ليس سالبًا أبدًا , لذلك على الأقل نحتاج إلى \(y \ge 0\).
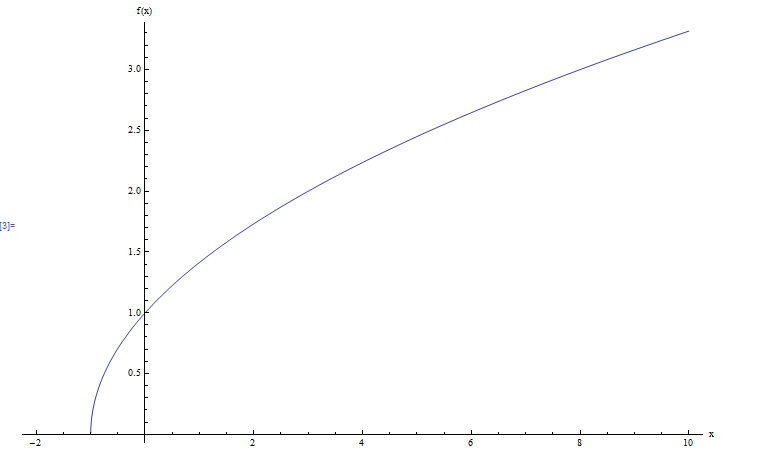
أيضًا , من خلال تطبيق المربع على كلا الجانبين , نحصل على \(x+1 = y^2\) , لذا فإن الحل هو \(x = y^2-1\). لذا , فإن القيد الوحيد الذي نحتاج إلى فرضه على \(y\) هو \(y \ge 0\). ومن ثم , باستخدام تدوين الفاصل الزمني , نكتب \(R(f) = [0, +\infty)\). بيانيا:
المزيد حول المجال والمدى
كطريقة للتلخيص , دعونا نلخص بعض الأشياء. أولاً , المجال هو المكان الذي يتم فيه تعريف الوظيفة بشكل جيد , والنطاق هو مجموعة النقاط التي يتم الوصول إليها من خلال الوظيفة.
من حيث الحسابات المطلوبة , عادةً ما يكون العثور على المجال أسهل من العثور على النطاق. عادةً ما يحاول بعض الأشخاص العثور على النطاق بيانياً , ولكن ربما تكون هذه طريقة أقل دقة. يجب تفسير الإجابات الرسومية بحذر.
يمكنك التحقق من البرامج التعليمية على وجه التحديد حول كيف تجد المجال و النطاق , والتي تركز بشكل خاص على كل حالة بمزيد من التفصيل.
