使用笛卡尔的符号规则

这个计算器将帮助你应用笛卡尔符号规则,对你提供的任何给定的多项式进行计算。它的唯一要求是该多项式必须是有效的。

例如,你可以提供简单的立方体多项式,如x^3 - 2x + 1,但你也可以提供更复杂的,如x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1,等等。

一旦你提供一个有效的 多项式函数 你点击 "计算 "按钮,以获得所有步骤的过程显示。

寻找多项式的零点 是代数中最重要的任务之一, 但在一般情况下这不是一项容易的任务.所有度数的多项式都没有通用的公式,所以我们通常要按照系统的程序,尽可能多地找到根。

在这种情况下,掌握尽可能多的关于根的类型的信息总是有用的,这也是笛卡尔符号规则的目标之一。

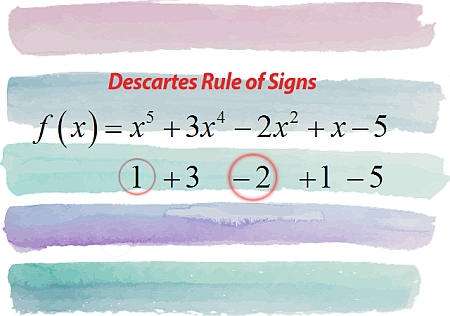
笛卡尔的符号规则说明了什么？

简单地说,笛卡尔符号法则告诉你关于多项式的正根和负根的数量,只需看一下给定的多项式系数的符号。

更确切地说,你从领先的系数开始,忽略零系数,然后去计算符号的变化。连续系数符号变化的总数是\(p(x)\)的正根数的上限,而 正根的数量 与符号变化的总数具有相同的奇偶性。

然后,你做同样的练习,但对于\(p(-x)\)的系数,你在这种情况下得到的是,连续系数的符号变化总数是\(p(x)\)的负根数的上限,并且 负根的数量 与符号变化的总数具有相同的奇偶性。

应用笛卡尔符号规则的步骤

• 步骤1： 确定你需要分析的多项式p(x)。确保它是一个多项式（否则该方法不起作用）,并尽可能地简化它
• 第2步： 将p(x)的系数放在一行中,从领先的系数开始,按降序排列,省略零系数
• 第 3 步： 从领先系数开始,计算连续系数之间的符号变化,并记下符号变化的总数,称之为T
• 第4步： p(x)的正零数最多为T,并且与T具有相同的奇偶性（如果T是偶数,那么p(x)的正零数是偶数,如果T是奇数,那么p(x)的正零数是奇数）。
• 第4步： 现在对p(-x)的系数重复同样的过程,以获得关于p(x)的负零数的信息。

这种方法可以给你正（和负）零数的可能范围,但它也可能告诉你一个给定的多项式有多少个正（或负）零,这只取决于你计算了多少个符号变化。

我可以用这种方法计算出实际的零点吗？

不,笛卡尔的符号法则并不是为了给你提供关于实际根是什么的信息,它只是告诉你一些关于正根（和负根）的数量。

现在,结合这些信息,以及 有理根定理 和其他初级工具,包括 合成部 和 因素定理 ,你将更有能力看清根部的实际价值。

技巧和窍门

始终如一 简化 首先是多项式。例如,如果你有\(p(x) = x^5 - x^3\),你会想先到\(p(x) = x^5 - x^3 = x^3(x^2 - 1)\),这样你就知道0是根（倍数为3）,然后你把笛卡尔规则应用到\(x^2 - 1\)。

例子。笛卡尔的符号规则

指出\(x^4 - x^3 + x^2 + 1\)的正根和负根的可能数量

解决方案： 我们得到了以下多项式函数。\(\displaystyle x^4 - x^3 + x^2 + 1\),对此我们需要应用笛卡尔符号规则。

积极的根基 :多项式系数（从高到低的功率）为：。

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

我们发现,连续的系数中符号变化的数量是。\(2\),变化是：\(\,\,+1\,\,\)和\(\,\,-1\,\,\),\(\,\,-1\,\,\)和\(\,\,+1\,\,\)。\(\,\,+1\,\,\)和\(\,\,-1\,\,\),\(\,\,-1\,\,\)和\(\,\,+1\,\,\)。

负数根 :\(p(-x) = x^4+x^3+x^2+1\)的多项式系数是。

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

没有发现\(p(-x)\)的系数有符号变化。

结论。 根据发现的符号变化数,即\(2\),我们得出结论：\(p(x)\)的\(p(x) = x^4-x^3+x^2+1\)可以有0或2个正根。

现在,由于\(p(-x)\)的系数没有发现符号变化,我们得出结论：\(p(x) = x^4-x^3+x^2+1\)没有负零。

例子。笛卡尔符号规则的更多内容

指出\(x^4 + x^3 + x^2 - 1\)的正根和负根的可能数量

解决方案： 现在我们需要分析\(\displaystyle x^4 + x^3 + x^2 - 1\),用笛卡尔的符号规则来分析。

所提供的表达式已经被简化,所以没有什么可以进一步简化的。

积极的根基 :系数为：。

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

观察一下,在这种情况下,连续系数的符号变化数等于\(1\),变化的内容是：\(\,\,+1\,\,\)和\(\,\,-1\,\,\)。\(\,\,+1\,\,\)和\(\,\,-1\,\,\)。

负数根 :与\(p(-x) = x^4-x^3+x^2-1\)相关的多项式系数是：。

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

然后,连续系数的符号变化数等于\(3\),变化情况为：\(\,\,+1\,\,\)和\(\,\,-1\,\,\)。\(\,\,+1\,\,\)和\(\,\,-1\,\,\),\(\,\,-1\,\,\)和\(\,\,+1\,\,\),\(\,\,+1\,\,\)和\(\,\,-1\,\,\)。

结论。 由于\(p(x)\)的系数中有一个符号变化,我们得出结论：\(p(x) = x^4+x^3+x^2-1\)正好有一个正零。

根据发现的符号变化的数量,即\(3\),我们得出结论：\(p(x) = x^4+x^3+x^2-1\)可能有1或3个负根。

例子。阳性和阴性符号

指出\(x^4 + 1\)的正根和负根的可能数量。你能说说正根和负根的确切数目吗？

解决方案： 在这种情况下,没有符号变化,所以也就没有正根。现在,\(p(-x) = (-x)^4 + 1 = x^4 + 1\),它没有符号变化,所以也没有负根。结论是多项式没有实根（因为0也不是根）。

更多多项式计算器

寻找多项式的根 是微积分和代数中大多数应用问题的中心点之一,是一项值得掌握的技能。

在计算多项式的零点时,有许多技巧,而 笛卡尔标志规则 给你提供了很多信息,这些信息可以通过观察多项式的系数来推断出来,非常简单。