有理函数
指示: 使用此有理函数计算器计算有理函数的截距和图形,并显示步骤。请输入您要计算的有理函数。
有理函数
通过这个有理函数计算器,您可以分析所提供有理函数的最相关点,并显示所有步骤。通常,对于大多数有理函数,您都可以找到截距,垂直渐近线及其图形。某些特定的有理函数还有水平渐近线。
您可以提供的函数类型有 "f(x)=1/x - x",或者涉及高次多项式的函数,如 "f(x) = (x^3-1)/(x^2+x)
提供有效的有理函数后,点击计算按钮,所有步骤都会显示出来。
有理函数的主要特性之一是,你可以将计算简化为以下问题 解多项式方程 这是一种 "最简单 "的 可以求解的方程 .

什么是有理函数
有理函数是一个涉及到 两多项式之商 \(P(x)\) 和 \(Q(x)\),其中除数 \(Q(x)\) 不等于零多项式。因此,有理函数公式为
\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]例如,函数
\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]是有理函数,因为它正是两个多项式的商。但例如
\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]不是有理数,因为除数不是多项式。请注意,当我们说除数 \(Q(x)\) 不等于零多项式时,并不是说 \(Q(x)\) 不能有零。例如,在 \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \) 这个例子中,除数是 \(Q(x) = x + 1\),它在 \(x = -1\) 处有一个零。
我们不希望出现以下情况
\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]因为虽然在这种情况下 \(Q(x) = 0\) 严格来说是一个多项式,但它是零多项式(在任何地方都为零)。
计算有理函数的步骤
- 步骤1: 首先,确保您确实有一个有理函数,您可以确定其分子 P(x) 和分母 Q(x)
- 第2步: 如果找不到严格意义上的上述结构,就停止。您可能需要通过 代数还原 .
- 第3步: 您需要找到 P(x) 和 Q(x) 的实数零点(如果有的话)。找到的结论将与 P(x) 和 Q(x) 的零点紧密相关
- 第4步: 要找到 y-截距,需要通过计算 f(0),在零点对函数进行求值。如果 x = 0 不是 Q(x) 的零点,y-截距的定义将非常明确
- 第5步: 要找到 x 截点,需要得到 P(x) 的零点,而这些零点不是 Q(x) 的零点
- 第6步。 要找到垂直渐近线,需要找到 Q(x) 的零点,这些零点不是 P(x) 的零点
- 第7步。 要找到水平渐近线,需要 Q(x) 的阶数大于或等于 P(x) 的阶数。
观察发现,正如所料,分析有理函数取决于 寻找多项式的零点 ......,然后把所有结论放在一起。.
请注意,有理函数的域是整条实线,除数 Q(x) 的零点除外。如果 Q(x) 的零点也是 P(x) 的零点,那么不连续点就可以修复。有理函数的范围取决于 P(x) 和 Q(x) 的度数。
为什么使用有理函数
使用有理函数是因为它们是多项式的自然延伸。我们可以把它们看作是函数复杂性的下一步。我们知道 多项式表达式 是我们能找到的最简单的函数之一,但也是最有用的函数之一。
有理方程通常会出现在更高级的混合问题中,但只要涉及的多项式足够简单,处理起来却出奇地简单。我们知道 如何解一元二次方程 但对于 3 度及以上的多项式,情况可能会更加棘手。

多项式函数也是有理函数吗?
是的,如果 P(x) 是多项式,那么 P(x) 也是有理数,因为我们可以这样写:
\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]而 Q(x) = 1 是一个实际的多项式。反之则不然:有理函数不一定是多项式。为什么会这样呢?因为自然地,除非 Q(x) = 1,否则只要有 \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \),就不会有多项式定义所要求的所有项都是自由项。
更正式地说,使用 剩余定理 我们有
\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]其中 \(d(x)\) 是多项式,但 \frac{r(x)}{Q(x)} 不是,因为 r(x) 的阶数小于 Q(x) 的阶数。

范例:使用有理函数
求...的截距,渐近线和图形:\(f(x) = \frac{x^2-1}{x+1}\)
解决方案:
我们获得了以下功能:
\[f\left(x\right)=\frac{x^2-1}{x+1}\]我们需要找到截距和渐近线(如果有的话)。之后,将呈现函数的图形。
让我们找出给定函数的零点。我们需要求解下面的有理方程:
\[\frac{x^2-1}{x+1}=0\]注意,对于 \(x \ne -1\),我们可以简化为
\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]辅助分母公式
现在,我们将分子设为零并找出解。那么,那些没有使分母等于零的根就是有理方程的解。
要找到分子的根,需要解决以下问题:\(x^2-1=0\)
对于形式为 \(a x^2 + bx + c = 0\) 的一元二次方程,根的计算公式如下:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]在这种情况下,我们需要求解的方程是 \(\displaystyle x^2-1 = 0\),这意味着相应的系数是:
\[a = 1\] \[b = 0\] \[c = -1\]首先,我们将计算判别式以评估根的性质。判别式的计算方法是:。
\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]因为在这种情况下,我们得到的判别式是 \(\Delta = \displaystyle 4 > 0\),是正值,所以我们知道方程有两个不同的实数根。
现在,将这些数值插入到根的公式中,我们可以得到。
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]因此,我们发现。
\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]辅助分母公式
我们需要找到分母的根:\(x+1=0\)
因此,对给定的线性方程求解 \(x\) 就会得到 \(x=-1\)。
分母和分子的零数
根据上述分析,给定有理函数分子的实零点为 \( x_{ 1} = -1\) 和 \( x_{ 2} = 1\)。
同时还发现分母有一个实数零,即 \( x_{ 1} = -1\)。
寻找 x 概念
根据分子的零点不是分母的零点,我们发现有一个 x 截距,即 \(\left(1, 0\right)\)。
寻找 y截距
通过评估 \(x = 0\) 提供的函数,我们发现
\[ f(0) = \frac{0^2-1}{0+1} = -1\]那么 y 的截距就是 \( \left(0, -1\right)\)。
垂直渐近线
分析零点后得出结论,函数没有垂直渐近线。
水平渐近线
注意到分子的阶数是 \(2\),分母的阶数是 \(1\),然后,由于分子中多项式的阶数超过了分母中多项式的阶数,我们得出结论:不存在水平渐近线。
得到下图
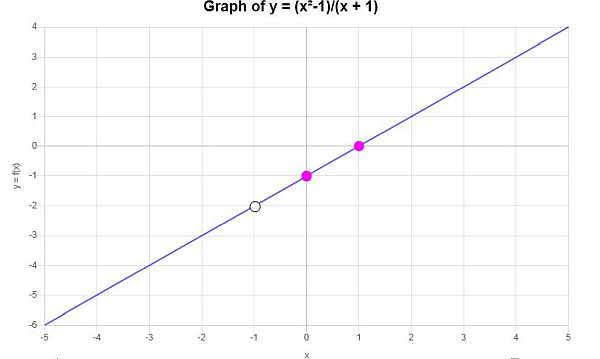
示例:水平渐近线水平渐近线
这个有理函数有水平渐近线吗?\(f(x) = \frac{x^2-1}{x^2+1}\)?
解决方案: 显然,在这种情况下,函数由两个多项式的商组成,它们的阶数都等于 2,即它们的阶数相同,因此存在水平渐近线。
我们也可以通过限制来看到这一点:
\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]这意味着水平渐近线是 \(y = 1\)。计算到此结束。
实用功能计算器
函数是基本的数学对象,它概括了不同变量之间的关系。使用 功能计算器 可以帮助你系统地处理那些过于复杂而无法手工处理的函数。
绘制有理函数图 是学生在代数和微积分中学习的最常见的玩具示例之一,虽然有理函数本身在应用中可能并不经常出现,但处理有理函数所需的分析技能却非常宝贵
同样 求解有理数方程 在这里,处理代数表达式并将其还原为低次项的原理将对掌握更高级的技能大有裨益。
现在,如果我们谈论功能,就不能忘记 函数导数的计算 ,积分和其他更高级的无穷小技术。




