微分计算器
指示: 使用此微分计算器,在您提供的给定点上找到您提供的函数的微分,显示所有步骤。请在下面的表格框中输入功能和点。
微分计算器
该计算器将允许您在您提供的点上计算您提供的函数的微分,显示过程的所有步骤。
您提供的函数可以是任何有效的可微分函数,例如 f(x) = x^2 + 2x 或 f(x) = x^2*sin(x),仅举两个示例。
然后,当您提供了微分计算的函数和点后,只需单击"计算"即可显示所有过程步骤。
的想法 微分 与切线紧密相连,并且 线性近似 ,因为微分精确地测量 y 的变化,沿着 切线 在给定点。
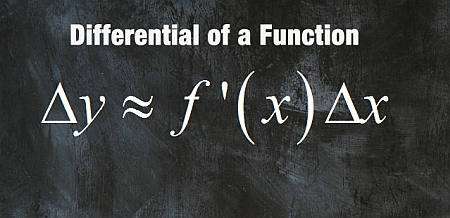
什么是微分?
在微分学中,导数为您提供有关函数在给定点的瞬时变化率的信息。
微分的概念使用 变化率 由给定点 \(x_0\) 处的导数确定,以通过其近似函数的行为 切线 .
微分的公式是基于这样的想法
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]其中 \(\Delta y = y - f(x_0)\) 和 \(\Delta x = x - x_0\)。对于微分\(dy\),我们定义
\[\displaystyle dy = f'(x_0) dx \]这个(松散的)定义基于以下想法:当 \(x\) 足够接近 \(x_0\) 时,线性近似和函数趋近于相同的行为。
计算微分的步骤
- 步骤1: 确定函数 f(x) 和要计算微分的点 x0
- 第2步: 计算导数 f'(x) 并在 x0 处计算它,因此您得到 f'(x0)。简化它,如果需要的话
- 第 3 步: 使用公式 \(\displaystyle dy = f'(x_0) dx \)
有时您会发现微分写为 \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \),表示您将使用微分来估计 y 的变化,由 \(\Delta y\) 测量。
微分计算器 dy
用一个 微分计算器 可以节省您计算导数的时间。差异的概念一直是一个奇怪的概念,因为它似乎被松散地定义了。
尽管有一种形式化定义微分及其运算的方法(称为微分形式的主题),但大多数数学家看不到微分存在的理由,因为它们没有提供任何新的信息,即导数或一阶近似不提供。
完全差异解释
微分最常见的应用和解释是在其"有限"表达式中使用时:
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]您希望根据 x 的变化(由 \(\Delta x\) 测量)和该点的导数来估计 y 的变化(由 \(\Delta y\) 测量)。
有时这个 \(\Delta y\) 被称为 总变差 或者 全差分 .
技巧和窍门
不要忘记微分可以作为理论定义,\(\displaystyle dy = f'(x_0) dx \),它表示由 x 的无穷小变化引起的 y 的无穷小变化。
它也可以以全微分形式使用,其中你有
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]当 x 发生变化(从 \(x_0\) 到 \(x\))时,它会告诉您 y 的近似变化。
所有代数计算器的中心是以分数的基本数字的力量为起点。
示例:微分计算器
考虑函数:\(f(x) = x^2\)。求其在\(x_0 = 1\)点的微分。
解决方案: 在第一个示例中,我们使用函数 \(\displaystyle f(x)=x^2\),为此我们需要计算它在点 \(x_0 = 1\) 处的微分。
该函数已经简化,所以我们可以直接计算其导数。
微分 :函数 \(\displaystyle f(x)=x^2\) 在点 \(x_0 = 1\) 的微分公式为:
\[dy = f'(x_0)(x - x_0) \]我们定义了 \(\displaystyle y_0 = f(x_0)\),因此在函数中插入点 \(x_0 = 1\) 的值会导致:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]另外,将\(x_0 = 1\)点的数值插入计算出的导数中,可以得出。
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]那么,我们现在将这个值代入微分公式得到:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]结论 :因此,我们发现函数 \(\displaystyle f(x)=x^2\) 在点 \(x_0 = 1\) 处的微分是:
\[dy = 2x-2 \]示例:微分计算
对于给定的函数:\(f(x) = x^3 + 3x^2 - 2\),在点\(x_0 = 2\)求微分。
解决方案: 现在,我们需要求微分的函数是 \(\displaystyle f(x)=x^3+3x^2-2\),
微分计算 :我们使用下面的公式来计算我们需要为给定函数 \(\displaystyle f(x)=x^3+3x^2-2\) 构造的微分,在给定点 \(x_0 = \frac{1}{2}\) 是:
\[dy = f'(x_0)(x - x_0) \]观察 \(\displaystyle y_0 = f(x_0)\),这意味着评估 \(x_0 = \frac{1}{2}\) 处的函数,我们发现:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]然后,我们得到在点\(x_0 = \frac{1}{2}\)处的导数:
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]因此,我们得到以下
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]结论 :最后的结论是,我们正在寻找的差异由以下公式给出:
\[dy = \frac{15}{4}x-\frac{15}{8} \]差分示例
我们得到函数:\(f(x) = \frac{\sin(x)}{x}\)。求其在\(x_0 = \frac{\pi}{2}\)点的微分。
解决方案:
提供了以下函数:\(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\),我们需要计算它在点\(x_0 = \frac{\pi}{2}\) 处的微分。
该函数已经简化,所以我们可以直接计算其导数。
计算 :现在是时候为给定点 \(x_0 = \frac{\pi}{2}\) 找到与 \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) 关联的微分了。使用的公式是:
\[dy = f'(x_0)(x - x_0) \]我们将点 \(x_0 = \frac{\pi}{2}\) 的值插入计算的导数中,这导致:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]因此,使用微分公式:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]结论 :对应的微分是:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]其他微分计算器
寻找衍生品 毫无疑问是微积分的关键要素。衍生工具提供了理解 变化率 的功能。因为它们有着密切的联系。
幸运的是,如果您遵循特定的规则,寻找衍生品是一个系统的过程(不一定容易) 差异化规则 .最常用的规则是 产品规则 , 商数规则 和 链条规则 .
线性或 一阶近似 从概念上尝试通过一条线来逼近一个函数,至少在局部,并且可以告诉你很多关于函数在某个点附近的行为。






