解答者代数

多项式不等式

指示： 使用多项式不等式计算器求解任何多项式不等式,显示过程的所有步骤。请在下面的框中输入多项式不等式。

多项式不等式的更多信息

这款计算器可以帮助您求解多项式不等式,向您展示求解计算过程的所有步骤,并为您提供不等式图,描述求解过程。

您提供的不等式可以是简单的 "x^2 > 1",也可以是更复杂的 "x^3 + 3x^2 + 3x + 1 > 0"。

一旦提供了有效的多项式不等式,请点击 "计算 "按钮,以获得解法和显示的所有步骤。

请注意,并非您提供的所有多项式都能找到精确解。多项式的度数越小,找到不等式精确解的可能性就越大。

什么是多项式不等式

多项式不等式是一种简单的不等式,其中涉及的表达式都是多项式,并且没有一个项是非多项式表达式。例如

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

是多项式不等式,而

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

不是多项式,因为其中有 \(\sin x\) 项。解不等式在一般情况下这是一个困难的过程,但对于多项式,我们有一个明确的行动计划。

如何求解多项式不等式

步骤1： 确保所有项都是多项式。否则,用于多项式的特定方法可能不适用
第2步： 把所有东西都放在一边,另一边为零
第3步： 用"="代替不等号,求解相关方程（这需要找到多项式的零点）
第4步： 收集不等式的所有临界点,在本例中,这些临界点就是辅助线的实零点。多项式方程 (在这种情况下不考虑复数根）。
第5步： 如果不存在临界点,则意味着表达式的符号不会改变,因此整条实线都是解,否则就是无解。检查时,选择任意一点,看它是否满足不等式,如果满足,则整条实线都是解,如果不满足,则没有解
第6步。 如果存在临界点,则构建具有连续临界点的区间（以 -∞ 作为起始临界点,以 ∞ 作为终止临界点）
第7步。 检查每一个区间,看看里面的点是否符合不等式。如果符合,则该区间是解的一部分；如果不符合,则该区间不是解的一部分。

这里的关键在于,临界点和我们从临界点推导出的区间都是表达式符号不变的区间,因此要么整个区间都是解,要么区间中的任何一点都不是解的一部分。

多项式零点和临界点

之所以可以求解多项式不等式,除了多项式是连续表达式之外,还因为分析多项式表达式的临界点相对简单。

会出现以下不平等现象

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

在这种情况下,要找到临界点将难上加难。线性不等式的临界点更简单,但也仅此而已。任何一般不等式都有其复杂性。

多项式在现实生活中的应用

多项式有很多应用。例如,在物理学中学习运动学时,就会从牛顿定律中得到一些有趣的多项式表达式。这些表达式可以定义物体位置的条件,从而得出一个多项式不等式,以确定物体在哪个时间段高于某个高度,这在弹道学等方面至关重要。

此外,在学习微分方程时,您可以发现方程中的倾覆项取决于一个幂,并且具有多项式结构,对此您可以使用一些高级不等式,如格伦沃尔不等式。

例题：解多项式不等式

解决：\(x^2 - x > \frac{1}{2}\)

解决方案：我们需要先求解下面给出的一元二次方程 \(\displaystyle x^2-x-\frac{1}{2}=0\)：

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

因此,我们发现。

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

关键点分析

发现的临界点列表按升序排列为\(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

在此基础上,我们需要对以下区间进行分析：

- 对于区间 \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\)：左侧为正,因此 \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) 是解的一部分。

- 对于区间 \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\)：左侧为负数,这意味着 \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) 不属于解的一部分。

- 对于区间 \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\)：左侧为正,这意味着 \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) 是解的一部分。

不等式的解决方案

根据所提供的不等式并分析临界点,我们发现不等式的解是\(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) 或 \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\)。

使用区间符号,可将解法写成

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]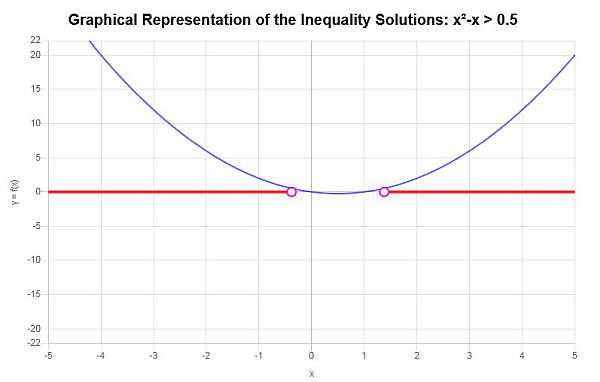

这就结束了计算。

例子高次多项式

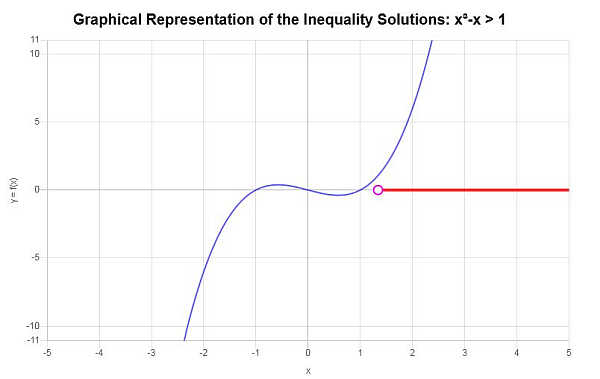
求解下面的不等式：\(x^3 - x > 1\)

解决方案：

为了解决 \(x^3-x > 1\),我们首先把所有东西都放在一边：

\[x^3-x-1> 0\]

由此,我们可以得到需要首先求解的相关方程,即 \(x^3-x-1=0\)。注意,度数是 \(\displaystyle deg(p) = 3\),前导系数是 \(\displaystyle a_{3} = 1\),常数系数是 \(\displaystyle a_0 = -1\)。

尝试合理的根源

我们先尝试用有理数零点定理找出简单的有理数根。

接下来的任务是找出前导系数 \(a_{3}\) 和常数系数 \(a_0\) 相除的整数,用来构建多项式方程的候选零点。

▹ \(a_{3} = 1\) 的分隔线是：\(\pm 1\)。

▹ \(a_0 = -1\) 的分隔线是：\(\pm 1\)。

因此,用常数系数 \(a_0 = -1\) 的每个除数除以前导系数 \(a_{3} = 1\) 的每个除数,我们会发现以下候选根的列表：

\[\pm \frac{ 1}{ 1}\]

现在,需要对所有的候选人进行测试,看他们是否是一个解决方案。以下是测试每个候选人得到的结果。

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:& & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:& & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

但由于我们没有通过检查找到任何有理根,我们不能用基本方法继续进行因式分解,所以这个过程在此停止。

可选 :这是一个度数为 \(3\) 的多项式,一共有 \(3\) 个根,即使有些根可能是复根,但在这种情况下,用基本方法找到的解少于 \(3\)。

利用先进的三次方程方法,可以发现完整的解集是

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

关键点分析

发现的唯一临界点是 \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\)。

在此基础上,我们需要对以下区间进行分析：

- 对于区间 \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\)：左侧为负数,因此 \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) 不是解的一部分。

- 对于区间 \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\)：左侧为正,这意味着 \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) 是解的一部分。