Калькулятор радикальных уравнений
Инструкции: Используйте этот калькулятор радикальных уравнений, чтобы решить любое предоставленное вами уравнение с радикалами, показывая все этапы процесса. Пожалуйста, введите радикальное уравнение, которое вы хотите решить, в поле ниже.
Решение радикальных уравнений
Этот решатель радикальных уравнений позволяет вам обрабатывать предоставленные вами радикальные уравнения, манипулируя ими алгебраически и показывая вам все этапы процесса.
Этот решатель примет любое допустимое уравнение, включающее корни, например, что-то действительно простое, например "sqrt(x) = 1", или что-то, что может быть намного сложнее решить, например, "sqrt(x+3) = x^2 - 1".
Как только будет предоставлено действительное радикальное уравнение, все, по сути, готово, и все, что останется сделать, это нажать "Решить", чтобы отобразить все этапы процесса.
Решение радикального уравнения сильно опирается на эффективный алгебраическая манипуляция с выражением , чтобы принципиально избавиться от радикальной части.

Что такое радикальное уравнение
Радикальное уравнение, если выражаться чрезвычайно просто, представляет собой разновидность математическое уравнение в котором неизвестное (обычно x) находится внутри радикала. Например
\[\displaystyle \sqrt x = x^2 \]является радикальным уравнением из-за члена \( \sqrt x\), но уравнение
\[\displaystyle 2 x = x^2 \]например, НЕ является радикальным уравнением, потому что мы не можем указать x внутри радикала где-либо в уравнении.
Как решить радикальные уравнения
Решить радикальные уравнения несложно, если выполнить следующие действия:
- Шаг 1: Во-первых, убедитесь, что вы имеете дело с радикальными уравнениями. Уравнения другого типа, скорее всего, будут решены по-другому
- Шаг 2: Упростите и сгруппируйте радикалы как можно больше, в идеале сосредоточив все в одном радикале
- Шаг 3: Примените мощность (обычно степень 2), чтобы устранить радикалы. Если вы все сделали правильно и уравнение поддается решению, вы сведете исходное уравнение к Полиномиальное уравнение .
- Шаг 4: Решите вспомогательную функцию и проверьте, какое из вспомогательных решений (если они есть) является решением исходного уравнения
Иногда, несмотря на соответствующую группировку и упрощение, полностью исключить радикалы не удастся или это приведет к еще более сложному уравнению.
Упрощение радикальных уравнений
Как мы упоминали выше, успешный расчет уравнений с корнями во многом зависит от умения Упростить радикалы . Но иногда этого бывает недостаточно, поскольку упрощение всех встречающихся радикалов не заставит их исчезнуть. Самый распространенный способ — уменьшить радикалы, а затем применить квадрат (степень 2) для отмены радикала.
Но возведение в квадрат ради избавления от радикала — это обоюдоострый меч, поскольку в результате возведения в квадрат любой значимый знак может исчезнуть. Именно поэтому при "устранении" радикала и нахождении решений вспомогательного уравнения мы ДОЛЖНЫ дважды проверить, что вспомогательные решения также являются решениями исходного уравнения. Часто это не так.

Другой способ увидеть процесс устранения радикала — использовать подходящую замену. Например, для радикального уравнения:
\[\displaystyle \sqrt x = x \]вы можете установить \(u = \sqrt x\), тогда \(u^2 = (\sqrt x)^2 = x\), тогда исходное уравнение превратится в следующее вспомогательное уравнение:
\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]это полиномиальное уравнение, которое мы можем решить. Итак, использование замены приводит к уравнению, которое мы не знаем, как решить, к решение полиномиального уравнения и мы знаем, кого решать.
Почему нас интересуют радикальные уравнения?
Радикальные уравнения часто встречаются в алгебре и исчислении, поскольку они лежат в основе моделирования множества различных явлений.
Радикальные функции интересны своими свойствами и типом медленного роста при стремлении x к бесконечности.

Пример. решение уравнений, включающих радикал
Решите следующее: \(\sqrt{x} = 2x\)
Решение:
Нам дано следующее уравнение. Нам нужно решить это уравнение, которое имеет только одну переменную, \(x\), поэтому цель состоит в том, чтобы найти \(x\):
\[\sqrt{x}=x^2\]Обратите внимание, что степень данного многочлена равна \(\displaystyle deg(p) = 4\), его старший коэффициент — \(\displaystyle a_{4} = -1\), а его постоянный коэффициент — \(\displaystyle a_0 = 0\).
Попытка найти рациональные корни
Кандидаты На Получение Рациональных Корней : Поскольку первый член с ненулевым коэффициентом в \(p(x)\) — это \(x\), мы можем вынести этот член, чтобы получить
\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]но член в скобках имеет степень больше 2, поэтому нет элементарной формулы для его умножения. Нам нужно проверить возможные рациональные корни.
Следующая задача — найти целые числа, которые делят старший коэффициент \(a_{3}\) и постоянный коэффициент \(a_0\), которые будут использоваться для построения наших кандидатов как нулей полиномиального уравнения.
▹ Разделители \(a_{3} = -1\): \(\pm 1\).
▹ Разделители \(a_0 = 1\): \(\pm 1\).
Следовательно, разделив каждый делитель постоянного коэффициента \(a_0 = 1\) на каждый делитель старшего коэффициента \(a_{3} = -1\), мы находим следующий список кандидатов в корни:
\[\pm \frac{ 1}{ 1}\]Теперь необходимо протестировать всех кандидатов, чтобы понять, являются ли они решением. В результате тестирования каждого кандидата получено следующее:
\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:& & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:& & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]Полиномиальное Деление : Поскольку у нас недостаточно корней среди рациональных кандидатов, мы разделим \(\displaystyle -x^3+1\) на произведение множителей, полученных из рациональных корней, то есть \(\displaystyle \left(x-1\right) \).
Шаг 1: Старший член делимого \(\displaystyle p(x) = -x^3+1\) — это \(\displaystyle -x^3\), тогда как старший член делителя \(\displaystyle s(x) = x-1\) равен \(\displaystyle x\).
Итак, член, который нам нужно умножить \(x\), чтобы получить главный член дивиденда, равен \(\displaystyle \frac{ -x^3}{ x} = -x^2\), поэтому мы добавляем этот член к частному. Кроме того, мы умножаем это на делитель, чтобы получить \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), который нам нужно вычесть из делимого:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]Шаг 2: Теперь главный член текущего остатка \(\displaystyle -x^2+1\) — это \(\displaystyle -x^2\), и мы знаем, что главный член делителя — \(\displaystyle x\).
Итак, член, который нам нужно умножить \(x\), чтобы получить главный член текущего остатка, равен \(\displaystyle \frac{ -x^2}{ x} = -x\), поэтому мы добавляем этот член к частному. Кроме того, мы умножаем это на делитель, чтобы получить \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), который нам нужно вычесть из текущего напоминания:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]Шаг 3: Теперь главный член текущего остатка \(\displaystyle -x+1\) — это \(\displaystyle -x\), и мы знаем, что главный член делителя — \(\displaystyle x\).
Итак, член, который нам нужно умножить \(x\), чтобы получить главный член текущего остатка, равен \(\displaystyle \frac{ -x}{ x} = -1\), поэтому мы добавляем этот член к частному. Кроме того, мы умножаем это на делитель, чтобы получить \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), который нам нужно вычесть из текущего напоминания:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]Следовательно, частное равно \(\displaystyle q(x) = -x^2-x-1\), а остаток — \(\displaystyle r(x) = 0\).
Таким образом, после деления мы продвинулись в факторизации с
\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]Но теперь, поскольку найденное частное \(\displaystyle -x^2-x-1\) является квадратичным, мы можем найти его корни и посмотреть, сможем ли мы факторизовать его в реальном поле.
Нам нужно решить следующее заданное квадратное уравнение \(\displaystyle -x^2-x-1=0\).
Использование квадратичной формулы
Для квадратного уравнения вида \(a x^2 + bx + c = 0\) корни вычисляются по следующей формуле:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]В этом случае нам нужно решить уравнение \(\displaystyle -x^2-x-1 = 0\), что означает, что соответствующие коэффициенты:
\[a = -1\] \[b = -1\] \[c = -1\]Сначала мы вычислим дискриминант, чтобы оценить природу корней. Дискриминант вычисляется как:
Поскольку в этом случае мы получаем дискриминант \(\Delta = \displaystyle -3 < 0\), который является отрицательным, мы знаем, что данное уравнение имеет два разных сопряженных комплексных корня.
Теперь, подставляя эти значения в формулу для корней, получаем:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]итак, мы выяснили, что:
\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]Таким образом, после нахождения корней последней квадратичной части мы находим два комплексных корня, поэтому мы не можем факторизовать член \(-x^2-x-1\) в действительном поле, поэтому мы заканчиваем процесс с помощью \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).
Заключение : Таким образом, окончательная факторизация, которую мы получаем, такова:
\[\displaystyle p(x) = -x^4+x = - x\left(x-1\right)\left(-x^2-x-1\right)\]Корнями, найденными с помощью процесса факторизации, являются \(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\) и \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\) .
Следовательно, решение \(x\) для данного полиномиального уравнения приводит к решениям \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\) с использованием методов факторизации.
Проверка вспомогательных решений
Проверка этих решений с помощью вспомогательного полиномиального уравнения показывает, что не все возможные решения на самом деле являются решением исходного уравнения. Единственными реальными решениями исходного уравнения являются:
\[x_1=0 \]\[x_2=1 \]
Следовательно, решение \(x\) для данного уравнения приводит к решениям \(x=0,\,\,x=1\).
Графически
Ниже приводится графическое представление полученных решений:
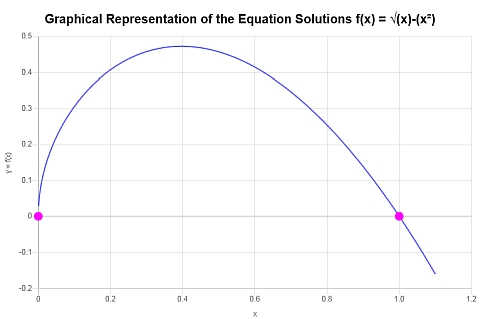
чем завершается расчет.
Другие полезные средства решения уравнений
При решении радикальных уравнений, в отличие от случая, когда нужно Решите линейные уравнения или когда тебе нужно решить квадратное уравнение , попадает в категорию тех уравнений, которые требуют столь умных алгебраических манипуляций, чтобы найти x.
Другими словами, у вас не будет вещи типа "делай так, и это всегда будет работать". Тип проводимых вами манипуляций будет зависеть от структуры уравнения и может сильно различаться от случая к случаю.
упрощение выражений использование первого варианта всегда является хорошей практикой, так как вы сократите члены, которые могут загромождать общую структуру уравнения.



