Калькулятор обратной функции
Инструкции: Используйте этот калькулятор, чтобы найти обратную функцию для предоставленной вами функции, показывая все шаги. Пожалуйста, введите выражение функции, для которой вы хотите найти обратную величину, в поле ниже.
Подробнее об этом калькуляторе обратной функции
Этот калькулятор позволит вам найти обратную функцию, показывая все шаги, предполагая, что обратная функция существует. Калькулятор проверит функцию решить уравнение связанный с определением функции, и он попытается оценить, существует ли обратная функция.
Например, вы можете предоставить линейную функцию типа "f(x) = 3x - 2", что будет простым случаем, или, например, вы можете поднять ее на ступеньку выше, применив что-то немного сложнее, например, с рациональной функцией, такой как 'y = (x-1)/(x-3)'.
После того, как вы предоставите действительную функцию, нажмите кнопку "Рассчитать", чтобы просмотреть все этапы процесса, показанные вам, с обратной функцией в качестве окончательного ответа, если обратная функция существует, или с объяснением, что решение не может быть найдено. и почему.
Не гарантируется, что вы найдете все обратные функции. Во-первых, не все функции имеют обратную, а во-вторых (как мы увидим в следующем разделе), процесс нахождения обратной функции включает в себя Решение для х для уравнения, а, как мы знаем, некоторые уравнения бывает очень сложно или невозможно решить.
Таким образом, более простые функции с большей вероятностью смогут найти свою инверсию, если инверсия существует.

Как определить обратную функцию?
С точки зрения непрофессионала, обратная функция — это функция, которая делает противоположное тому, что делает исходная функция. Итак, подумайте о функции в терминах y = f(x), а затем вы можете думать о ней при переходе от x к y. Вы передаете функции x, и функция дает вам конкретный y.
Обратная функция начинается с y и находит путь обратно к x таким образом, чтобы x был тем же самым, который привел к y через исходную функцию. Теперь формальное определение осуществляется через композиция функций . Для функции \(f\) мы говорим, что \(g\) является обратной функцией \(f\), если
\[ f(g(x)) = x \]и
\[ g(f(x)) = x \]для всех x в определенном наборе. Это еще не все, но мы оставим это на интуитивном уровне (Строго говоря, функция должна быть инъективной и сюръективной, чтобы быть обратимой, а также некоторые другие технические детали, которые необходимо учитывать, например, ограничение домен и диапазон , и т. д.)
Обычно мы вызываем \(f^{-1}\) для обратного \(f\), поэтому формула, определяющая обратную, обычно записывается как:
\[ f(f^{-1}(x)) = x \]Каковы действия по нахождению обратной функции?
- Шаг 1: Начните с уравнения, которое определяет функцию, то есть вы начинаете с y = f(x)
- Шаг 2: Затем вы используете алгебраические манипуляции, чтобы найти x. В зависимости от того, насколько сложна функция f(x), решение для x может оказаться проще или сложнее.
- Шаг 3: В некоторых случаях вы просто не сможете найти x для сложных нелинейных функций f(x)
- Шаг 4: Если вы можете найти x, то вы сможете написать x = g(y)
- Шаг 5: Вам необходимо оценить, является ли найденное решение уникальным. Это значит, что можно однозначно решить проблему x. Другими словами, нашли ли вы только одно решение при решении задачи x? Если да, то у вас есть обратная функция, в противном случае обратной функции нет
- Шаг 6: Если вы нашли обратное, решив x = g(y), вы просто измените имя переменной и напишите f -1 (x) = g(x), что делает акцент на том, что g(x) ЯВЛЯЕТСЯ фактически обратным
Если бы вы использовали исчисление и производные (но заметьте, что вам НЕ нужно Деривативы для вычисления обратной), вы можете найти производную функции и убедиться, что производная всегда положительна или отрицательна, чтобы гарантировать, что функция инъективна и, следовательно, обратима.
Но обычно методология Решение для х гораздо более приемлем для студентов, изучающих базовую алгебру.
Правило нахождения обратных функций
На самом деле не существует других правил для вычисления обратной функции, кроме как начать с y = f(x) и затем найти x. Подобное правило звучит довольно широко, потому что это так. Это больше, чем правило, это общая методология для начала процесса.
В конечном итоге вычисление обратного будет зависеть от вашего успеха в решении уравнения и уверенности в том, что решение уникально. Это помогает заранее оценить график функции, чтобы не искать обратную функцию, когда ее явно нет.
Что смотреть на графике? Чтобы функция была обратимой, она должна быть монотонной (возрастающей или убывающей) в определенной подобласти. С учетом вышесказанного мы могли бы удобно ограничить область определения функции меньшей подобластью, чтобы найти обратную функцию в меньшем наборе, что всегда возможно.

Как узнать наверняка, что функция имеет обратную?
Формально единственный способ убедиться, что функция имеет обратную функцию, — это убедиться, что функция инъективна (1 к 1). Это оценивается либо путем вычисления ее производной (если она существует) и проверки того, что она везде либо положительна, либо отрицательна, либо путем ручного обеспечения того, что, когда мы начинаем с y = f(x) и решаем для x, мы всегда получаем уникальное значение. решение.
Это также можно увидеть графически, используя тест горизонтальной линии: вы рисуете произвольную горизонтальную линию, и функция f(x) проходит тест горизонтальной линии, если какая-либо нарисованная горизонтальная линия пересекает график функции не более одного раза.

Пример: нахождение обратной функции
Найдите обратную функцию: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Решение:
У нас есть следующая функция:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Затем, чтобы найти обратную заданную функцию, нам нужно найти \(x\) и определить, существует решение или нет. Исходное уравнение:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Шаг 0: В этом случае нам сначала необходимо упростить данное линейное уравнение, и для этого мы проводим следующие шаги упрощения:
Решение линейного уравнения
Поместив \(x\) слева и \(y\) и константу справа, мы получим
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Теперь, решая \(x\), разделив обе части уравнения на \(-\frac{1}{3}\), получаем следующее:
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]и упрощая окончательно получаем следующее
\[\displaystyle x=3y-\frac{15}{4}\]Следовательно, решение \(y\) для данного линейного уравнения приводит к \(x=3y-\frac{15}{4}\).
Следовательно, и поскольку при решении \(x\) мы находим решение, и это только одно решение, мы нашли обратное.
Обратная функция
На основании показанной выше работы можно сделать вывод, что обратная функция имеет вид:
\[f^{-1}(x) = 3x-\frac{15}{4}\]Графически обратную функцию можно изобразить следующим образом:
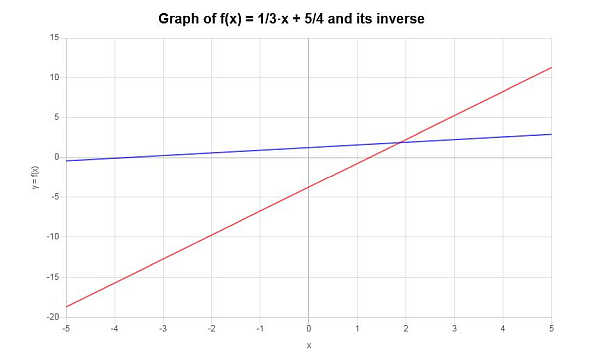
Пример: еще обратные примеры
Вычислите обратную функцию: \(y = \frac{x-1}{x+3}\)
Решение:
Чтобы найти обратную заданную функцию, мы находим \(x\) и определяем, существует решение или нет. Исходное уравнение:
\[y=\frac{x-1}{x+3}\]Получается следующее:
Вспомогательное уравнение числителя
Нам нужно приравнять числитель нулю и найти решения. Тогда те корни, которые не приводят знаменатель к нулю, будут решениями рационального уравнения
Используя алгебраические манипуляции с приведенным выше полиномиальным уравнением, получается следующее:
\[x = -\frac{3y+1}{y-1} \]Вспомогательное уравнение знаменателя
Находим корни знаменателя: \(x+3=0\)
Следовательно, решение \(x\) для данного линейного уравнения приводит к \(x=-3\).
Собираем решения рационального уравнения
Затем, проверив, что у нас нет нуля в знаменателе, мы находим следующее решение уравнения \(\displaystyle y=\frac{x-1}{x+3}\):
\[x = -\frac{3y+1}{y-1} \]Поскольку, решая \(x\), мы находим одно и только одно решение, мы заключаем, что у нас есть обратная функция.
Нахождение обратной функции
На основании показанной выше работы можно сделать вывод, что обратная функция имеет вид:
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]Найденную обратную функцию можно изобразить графически следующим образом:
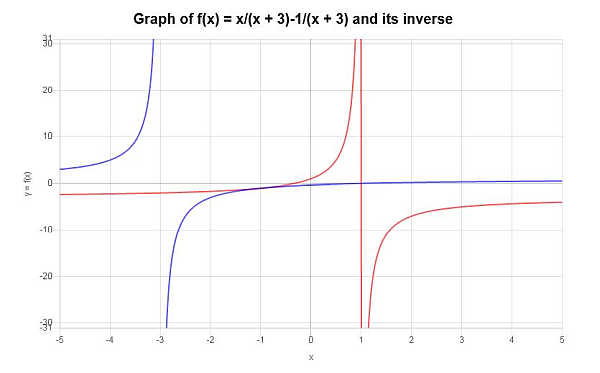
Пример. не все функции имеют обратные значения
Имеет ли следующая функция обратную: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Решение: Обратите внимание, что
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]что указывает на то, что существует два решения, и тогда обратного в этом случае нет.
Другие калькуляторы функций
Функции — важнейший объект в математике, особенно в исчислении и алгебре, где множество ассоциаций между переменными устанавливаются с помощью функций.
С функцией можно делать множество вещей: вы можете упростить их вы можете дифференцировать функцию , вы можете ими управлять, найти композицию с другой функцией, и список можно продолжать.
Во многих случаях, даже если вы явно упоминаете функции, у вас есть функции, лежащие в основе всего процесса. Итак, они есть, даже если иногда вы этого не знаете. Замечательно то, что даже в очень сложных случаях вы всегда можете построить график функции чтобы получить представление о ее поведении, чтобы хотя бы получить представление о том, что делает функция (повышается, понижается и т. д.).




