More About the Cross Product Calculator

This calculator will allow you to compute the cross product of two vectors . All you need to do is to provide the two vectors for which you wish to calculate the cross product.

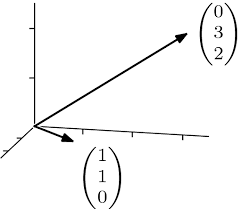
The cross product is an operation conducted for two three dimensional vectors \(x = (x_1,x_2,x_3)\) and \(y = (y_1, y_2, y_3)\), and the result of the operation is a three dimensional vector.

Cross Product Formula

The cross product method of calculation is not too complicated and it is actually very mnemonic. The formula for the cross product is shown below:

\[ x \times y = \left| \begin{matrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\ {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\ \end{matrix} \right| \]

This formula, expressed as a 3x3 determinant, is perhaps the easiest one to memorize. The formula that specifically refers to the components \(x_{ij}\) and \(y_{ij}\) are a lot harder to remember.

This could be generalized for a cross product in 4d, but that goes beyond the scope of this calculator, where we only deal with 3d calculations.

Cross Product Interpretation

The cross product has a strong geometric motivation. First of all, the cross product is a vector product, which means that you provide two vectors, and the result is another vector.

Indeed, the cross product corresponds to a vector with magnitude equal to the area of the parallelogram formed by the vectors \(x\) and \(y\).

Also, the resulting vector has a direction that is perpendicular to the plane formed by the vectors \(x\) and \(y\).

So indeed, the cross product has a 3d representation, first by the parallelogram expressed by the two vectors, and the vector that is perpendicular to it.

The cross product and the dot product

A related operation for two vectors is the dot product , although the output of a dot product is a scalar and not a vector. The cross product and the dot product are related in many aspects, but are used in different contexts.

So, aside from this vector cross product calculator, you have a scalar product represented by the dot product.