حلول حساب التفاضل والتكامل

مشتقات الثلاثية العكسية

عاليما: Use this calculator to find derivatives of inverse trig functions, showing all the steps. Please type the function that contains an inverse trig function in the form box below.

مشتقات الثلاثية العكسية

With this calculator you will be able to compute derivatives of inverse trig functions, showing all the steps of the process.

The idea is that the function you provide contains an inverse trig function, for example f(x) = x^2/arctan(x+1), just to give an example.

عندما تكون جاهزًا وتنتهي في كتابة الوظيفة التي تحتاجها للتمييز , انقر فوق الزر "حساب" من أجل رؤية جميع خطوات العملية والحسابات.

فكرة حstab tlmشtقaT من وظائف المثلثات العكسية هي طبيعية , وسنرى في الفقرات التالية أنه يمكن اشتقاقها مباشرة من mشtقat ثlaثyة الذي تعرفه.

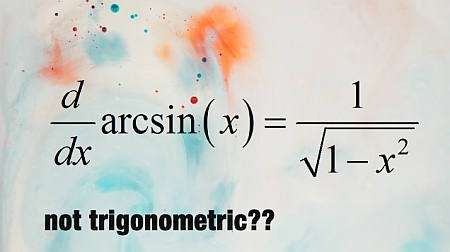
وظائف المثلثات العكسية

بعبارات بسيطة , فإن وظيفة المثلثات العكسية هي تلك الوظيفة التي عند تقييمها في وظيفة TRIG المقابلة , فإنها تؤدي إلى الهوية.على سبيل المثال , إذا نظرنا إلى الوظيفة \(\sin(x)\) , فإن وظيفتها العكسية هي \(\arcsin(x)\) , وهذا العكسي له خاصية

\[\sin(\arcsin(x)) = x \]

إلى جانب

\[\arcsin(\sin(x)) = x \]

for all \(x\) on a certain interval. So strictly, \(\arcsin(x)\) is the inverse function of \(\sin(x)\) from an algebraic point of view. And the same goes for the other inverse trig functions and their corresponding trig functions.

حساب مشتقات المثلثات العكسية

So then, if \(f\) is a function, and it has an inverse \(f^{-1}\), then we have that

\[f^{-1}(f(x)) = x\]

للجميع \(x\).ثم , إذا قمنا بتمييز جانبي المساواة , وقمنا باستخدام قاعدة السلسلة على الجانب الأيسر , نحصل عليها

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

الآن , إذا قمنا بتعيين \(y = f(x)\) , ثم \(x = f^{-1}(y)\) , مما يؤدي إلى

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

كيف نستخدم هذا لوظائف المثلثات العكسية؟افترض \(f(x) = \sin(x)\) و \(f^{-1}(x) = \arcsin(x)\).ثم , وفقًا للعلاقة العامة بين مشتق الوظيفة ومشتق عكسها , نحصل على

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

لكن الخدعة الهندسية الأنيقة تخبرنا بذلك

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

which implies that

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

يتم الحصول على بقية مشتقات المثلثات العكسية بحجة مماثلة.

ما هي وظائف الثلاثية العكسية الأساسية 6؟

#1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
#2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
#3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
#4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
#5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
#6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

ومن المثير للاهتمام , عند حساب مشتق وظائف المثلثات العكسية , لا تتضمن أي من مشتقات TRIG العكسية إما وظائف TRIG أو وظائف TRIG العكسية.

تطبيقات مشتق من الوظائف المثلثية العكسية

تشكل وظائف TRIG ومشتقاتها , وكذلك وظائف TRIG العكسية ومشتقاتها جزءًا من جرد الوظائف والعمليات الأساسية , المستخدمة كبنات بناء , لإنشاء وظائف أكثر تعقيدًا.

على الرغم من أن وظائف TRIG ستظهر في كثير من الأحيان في التطبيقات أكثر من وظائف TRIG العكسية , فإن الأخير أيضًا مكان واضح في حساب التفاضل والتكامل , خاصة عند التمييز بين طريقة تحلل الكسور الجزئية واستخدامها.

النصائح والحيل

لا تنس أن مشتقات وظائف المثلثات العكسية يمكن أن تكون مفيدة للغاية , خاصة عند دمج المصطلحات التي لها قاسم تربيعي.

وأيضًا , من السهل ارتكاب أخطاء عند حساب مشتقات المثلثات العكسية بحكم التعريف , يمكنك بالتأكيد الاستفادة من استخدام أ حaSbة mشtقة سيظهر ذلك الخطوات , أو يمكنك استخدامه للتحقق من عملك.

مثال: مشتقات الثلاثية العكسية

احسب مشتق: \(f(x) = x + \arcsin(x^2)\)

الملم: لهذا المثال الأول , سنقوم بتحليل \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\).تتضمن هذه الوظيفة وظيفة ثلاثية عكسية , تتفاقم مع وظيفة أخرى.دعونا نحسب مشتقها:

\( \displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

But we know already that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

By using the Chain Rule: \(\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}\)

إجabة : يمكننا أن نستنتج أن مشتق الوظيفة هو:

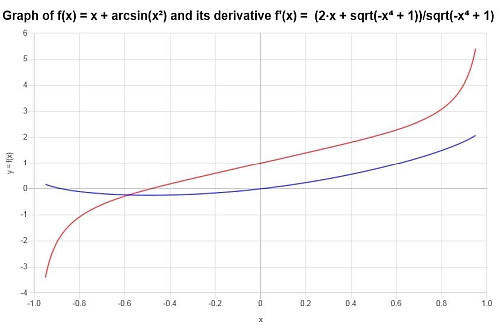
\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

يمكننا أن نرى كل من الوظيفة ومشتقها في الرسم البياني التالي:

مثال: المزيد من مشتقات المثلثات العكسية

النظر في الوظيفة التالية: \(f(x) = \frac{\arcsin(x)}{x}\) , احسب مشتقها.

الملم: الآن للمثال الثاني , لدينا وظيفة \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

\( \displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)\)

The Quotient Rule applies in this case: \(\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\)

الإرهاق : The derivative we are looking for is:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

بيانياً , لدينا ما يلي:

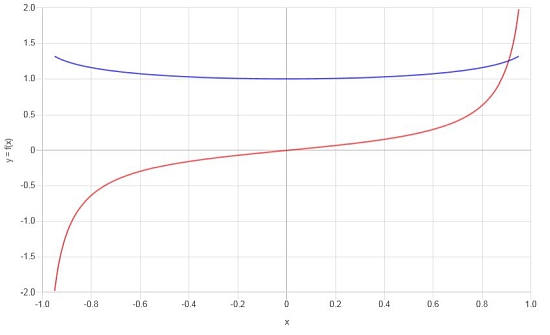
مثال على مشتقات المثلثات العكسية

احسب مشتق: \(f(x) = x \arctan(x+1)\)

الملم: الآن لهذا المثال الأخير , سنعمل مع الوظيفة \(\displaystyle f(x)=x\arctan\left(x+1\right)\) , والتي تحتوي على وظيفة عكسية.

\( \displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)\)

The Product Rule applies in this case: \(\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)\)

We expand the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Reducing the one in \(x\cdot 1 = x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\)

تاسنتا : بعد التبسيط , المشتق هو:

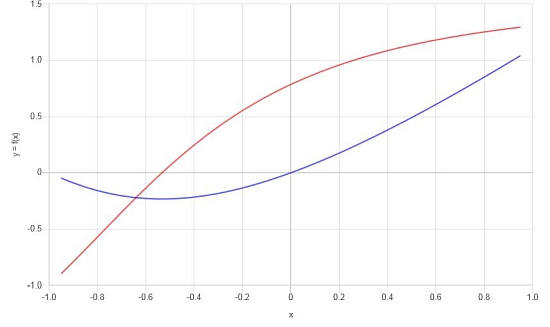
\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

بناءً على النتائج الموجودة , يمكننا إنشاء الرسم البياني التالي لـ F و F ':

Other calculus calculators

عند استخدام mشtقat ثlaثyة , ذكرنا أنها كانت لبنات بناء حاسمة لتطبيق الأساسي قoaudd amشtقة وبعد

Derivatives for inverse trig functions can be derived simply from the المجموع of basic trig derivatives, and that is why we also consider them within the group of basic derivatives to learn or even memorize.