الرسم البياني لعدم المساواة
عاليمت: يمكنك استخدام هذه الآلة الحاسبة لتمثيل أي متباينة تقدمها, موضحًا جميع خطوات الحل. من فضلك اكتب المتباينة التي تريد رسمها بيانيا وحلها في المربع أدناه.
حول هذا الرسم البياني عدم المساواة
ستساعدك هذه الآلة الحاسبة في إيجاد الحل والرسم البياني لأي متباينة عامة, مع توضيح جميع الخطوات. يتعين عليك توفير متباينة صالحة لمتغير واحد (x), عن طريق كتابتها في المربع الموجود.
على سبيل المثال, يمكنك توفير متباينة خطية بسيطة مثل '3x - 1 < 1/3', أو شيء مثل '2x-x^2 <= 3/4', والذي يتوافق مع متباينة تربيعية.
بمجرد تقديم المتباينة التي تريد رسمها بيانيًا, تابع وانقر على زر "حل", حتى يتم تقديم الحلول لك, مع جميع الخطوات, في حال كان من الممكن العثور على حلول.
حل المعادلات العامة والتفاوتات العامة مهمة صعبة بشكل عام, باستثناء مجموعة محددة من الهياكل القابلة للمعالجة المنهجية.
بعض الأنواع القليلة التي تسمح بالحل الدقيق هي المتباينات الخطية و المتباينات متعددة الحدود .
أحد الأنواع المهمة من المتباينات التي ترغب في حلها هو حالة المتباينات العقلانية, حيث يمكنك تحديد خارج قسمة كثيرات الحدود. تعتبر أوجه عدم المساواة هذه مثيرة للاهتمام نظرًا لوجود تقسيمات محتملة على الصفر والتي تحتاج إلى معالجة. يمكن بسهولة توسيع فكرة المتباينة العقلانية لتشمل حاصل الدوال بشكل عام, وليس بالضرورة كثيرات الحدود
كيفية رسم بياني لعدم المساواة
أبسط إجابة لذلك هي: لتمثيل المتباينة بيانيًا, عليك أن تعرف كيفية حلها. عادةً ما يتم تمثيل الحل الرسومي للمتباينة على شكل فاصل زمني أو عدة فترات متصلة على المحور x.
إذن, بعد أن ذكرنا ذلك, فإن رسم المتباينة بيانيًا سيبدأ بحلها أولًا, وهو ما يتضمن إيجاد مجموعة من القيم في الخط الحقيقي التي تحقق المتباينة المقدمة.
يمكنك تقديم الرسم البياني كفترة مستقلة, أو يمكنك رسم حلول المتباينة مع الرسم البياني للتعبير الذي يكمن وراء المتباينة: دعونا نتذكر ذلك من أجل حل عدم المساواة , تقوم بتمرير جميع الحدود إلى جانب واحد (مما يمنحك التعبير الأساسي) وحل معادلة مساعدة
خطوات حل المتباينات ورسمها بيانيًا
- الظهر 1: مرر كل الحدود إلى جانب واحد, بحيث يكون لديك تعبير واحد في أحد الجانبين, ويكون لديك صفر في الجانب الآخر
- ال alخطoة 2: من المتباينة (عندما يكون كل شيء في أحد الطرفين وصفرًا في الجانب الآخر), أنشئ معادلة مساعدة
- الله 3: حل هذه المعادلة بطريقة مناسبة لبنيتها (تتطلب الأنواع المختلفة من المعادلات تقنيات وأساليب محددة)
- الظهر 4: بناءً على الحلول الحقيقية للمعادلات المساعدة (الحلول الحقيقية بدلاً من الحلول المعقدة), يمكنك إنشاء نقاطك الحرجة وترتيبها بترتيب تصاعدي
- الظهر 5: تحتاج أيضًا إلى البحث عن النقاط التي يكون فيها التعبير غير محدد. إحدى الحالات البارزة لهذا تحدث مع المتباينات الكسرية, حيث يكون لديك مقام متعدد الحدود, وبالتالي فإن التعبير سيكون غير محدد على أصفار المقام. لذلك تقوم بإضافة أصفار المقام إلى قائمة النقاط الحرجة
- ال 6: باستخدام نقاطك الحرجة, يمكنك إنشاء فترات زمنية باستخدام نقاط حرجة متتالية (باستخدام -∞ و∞ كنقطتي البداية والنهاية الحرجة)
- الظهر 7: في كل فترة, حلل إشارة التعبير ولاحظ ما إذا كانت متوافقة مع إشارة المتراجحة. إذا كان الأمر كذلك, فستكون الفترة جزءًا من الحل الشامل للمتباينة
يعد استخدام النقاط الحرجة للتحليل أمرًا في غاية الأهمية, لأنك بهذه الطريقة تكون متأكدًا من أن التعبير لا يغير الإشارات خلال كل فترة زمنية, بحيث تقتصر المشكلة على تقييم ما إذا كانت المتراجحة قد تم حلها لكل فترة من تلك الفترات الحرجة.
لجعل الأمر ملموسًا أكثر قليلًا, لديك بعض المتباينات المعطاة, ثم قمت بتمرير كل شيء إلى جانب واحد, بحيث يكون لديك شيء على شكل \(f(x) \le 0\). على سبيل المثال, يمكن أن يكون هذا شيئًا مثل \(x^2 - x + 1 \le 0\).
ومن ثم تأخذ \(f(x) \le 0\) وتجد المعادلة المساعدة \(f(x) = 0\). تأخذ التعبير \(f(x)\) وتجد أن أصفاره هي النقاط الحرجة. ولكنك لا تفعل ذلك فحسب, بل ترى أيضًا ما إذا كان \(f(x)\) غير محدد في أي مكان (القسمة على صفر, وما إلى ذلك). ربما يتم تعريفه في كل مكان, كما في الحالة \(x^2 - x + 1\), ولكن إذا وجدت نقاطًا حيث يكون التعبير غير محدد, فيمكنك إضافته إلى قائمة النقاط الحرجة.
ثم تقوم بإنشاء فترات زمنية بناءً على نقاط حرجة متتالية. بالنسبة لـ \(f(x) \le 0\), سوف تأخذ كجزء من الحلول تلك الفواصل الزمنية التي تكون فيها قيمة التعبير سالبة. إذا كانت المتراجحة الأصلية \(f(x) \ge 0\) فستأخذ كجزء من الحلول تلك الفترات التي تكون فيها قيمة التعبير موجبة
كيف يعمل هذا الرسم البياني لعدم المساواة
سيهتم مصممنا البياني للمتباينات عبر الإنترنت بواحدة من أكثر العمليات تعقيدًا في الجبر الأساسي, والتي تتعامل مع إيجاد حلول المتباينات ورسمها بيانيًا. إحدى المزايا الكبيرة للآلة الحاسبة لدينا هي أنها ستعرض جميع الخطوات, عندما يكون ذلك ممكنًا.
أولاً, سوف يحل الرسم البياني المتراجحة عن طريق حل معادلة مساعدة مناسبة أولاً. تتطلب هذه العملية الكشف عن هياكل معروفة محددة, حيث من المحتمل أن تتطلب جميع الهياكل أساليب مختلفة. على سبيل المثال, لحل متباينة عقلانية (والتي تتضمن حاصل قسمة كثيرتي الحدود) مثل على سبيل المثال
\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]سوف تحتاج إلى طريقة مختلفة عن تلك المستخدمة لحل المتباينة التربيعية مثل \(x^2 + 3x < 1\), على سبيل المثال, وستأخذ هذه الآلة الحاسبة كل هذه التفاصيل

إذا لم يتم الكشف عن بنية تقليدية أو معروفة بشكل شائع, فسيتم استخدام بدائل مختلفة شائعة الاستخدام, على سبيل المثال \(u = \sqrt x\) أو \(u = \sin x\). إذا لم ينجح أي شيء, فستحاول الآلة الحاسبة إيجاد الحلول عن طريق الفحص والرقم, حتى تحصل على فكرة عن الحلول على الأقل.
كيف يمكنك تقديم رسم بياني لعدم المساواة؟
كما ذكرنا أعلاه, فهي ليست مكتوبة حقًا على الحجر, ولكن الطريقة الأكثر شيوعًا هي رسم بياني للتعبير الأساسي عن المتراجحة, وتسليط الضوء على قيم x التي تحقق المتراجحة. ربما يكون هذا هو أفضل تنسيق رسومي لهذا الغرض, وهو ما يستخدمه هذا الرسم البياني.
يمكنك أيضًا رسم كائن فاصل مستقل, لكن ربما يكون هذا أقل دلالة, لأنه يفقد منظور ما يحدث بالفعل مع المتراجحة نفسها.

مثال: رسم بياني لعدم المساواة
ارسم بيانيًا عدم المساواة التالية: \(\frac{1}{x}+x > 1\)
إل: لدينا عدم المساواة التالية التي تحتاج إلى حل:
\[\frac{1}{x}+x > 1\]نحن بحاجة إلى وضع جميع شروط عدم المساواة في جانب واحد:
\[x+\frac{1}{x}-1>0\]حل المعادلة المساعدة
من عدم المساواة أعلاه, نحصل على المعادلة المرتبطة التي يجب حلها أولا:
\[x+\frac{1}{x}-1=0\]تحليل النقاط الحرجة
نحن بحاجة إلى تنظيم النقاط الحرجة الموجودة (من الجذور الحقيقية للبسط والمقام) بترتيب تصاعدي, وتحديد الفترات مع جميع النقاط الحرجة المتتالية, وتقييم إشارة الحجم الأيسر للمتباينة في كل من تلك الفترات .
النقطة الحرجة الوحيدة التي تم العثور عليها هي \(0\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للمجال \(\left(-\infty, 0\right)\): البسط موجب والمقام سالب, وبالتالي يكون الطرف الأيسر سالباً, مما يعني أن \(\left(-\infty, 0\right)\) ليس جزءاً من الحل.
• بالنسبة للفاصل \(\left(0, \infty\right)\): البسط موجب والمقام موجب, فالطرف الأيسر موجب, إذن \(\left(0, \infty\right)\) جزء من الحل.
حل عدم المساواة
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x > 0\).
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left(0,\infty\right)\]يتم الحصول على ما يلي مع الرسم البياني عدم المساواة:
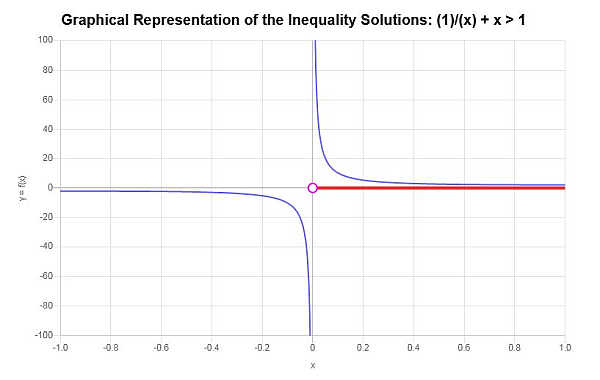
الذي يختتم الحساب.
مثال: رسم بياني لمتباينات كثيرات الحدود
أوجد الرسم البياني لعدم المساواة: \(x^2 - 2x \ge 4\)
حل:
نحن بحاجة إلى وضع جميع شروط عدم المساواة في جانب واحد:
\[x^2-2x-4\ge0\]حل المعادلة المساعدة
من عدم المساواة أعلاه, نحصل على المعادلة المرتبطة التي يجب حلها أولا:
\[x^2-2x-4=0\]باستخدام الصيغة التربيعية
للمعادلة التربيعية للنموذج \(a x^2 + bx + c = 0\), يتم حساب الجذور باستخدام الصيغة التالية:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]في هذه الحالة , لدينا أن المعادلة التي نحتاج إلى حلها هي \(\displaystyle x^2-2x-4 = 0\), مما يعني أن المعاملات المقابلة هي:
\[a = 1\] \[b = -2\] \[c = -4\]أولاً , سنحسب التمييز لتقييم طبيعة الجذور.يتم حساب التمييز على النحو التالي:
\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]لأنه في هذه الحالة , نحصل على التمييز هو \(\Delta = \displaystyle 20 > 0\), وهو أمر إيجابي , نعلم أن المعادلة لها جذور حقيقية مختلفة.
الآن , توصيل هذه القيم في صيغة الجذور التي نحصل عليها:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]إذن , نجد ذلك:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]في هذه الحالة , فإن المعادلة التربيعية \( \displaystyle x^2-2x-4 = 0 \), لها جذور حقيقية , إذن:
\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]إذن , يتم أخذ متعدد الحدود الأصلي في الحسبان كـ \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), والذي يكمل العوامل.
تحليل النقاط الحرجة
قائمة النقاط الحرجة التي تم العثور عليها منظمة بترتيب تصاعدي هي: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للفاصل \(\left(-\infty, -\sqrt{5}+1\right)\): الطرف الأيسر موجب, إذن \(\left(-\infty, -\sqrt{5}+1\right)\) جزء من الحل.
• بالنسبة للمجال \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): الطرف الأيسر سالب, إذن \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(\sqrt{5}+1, \infty\right)\): الجانب الأيسر موجب, مما يعني أن \(\left(\sqrt{5}+1, \infty\right)\) جزء من الحل.
حل عدم المساواة
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x \le -\sqrt{5}+1\) أو \(x \ge \sqrt{5}+1\).
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]بيانياً:
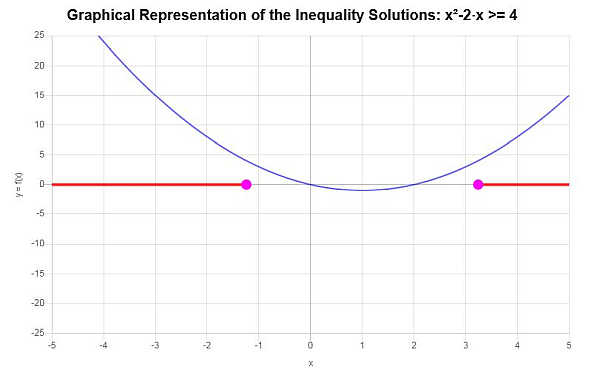
الذي يختتم الحساب.
المزيد من الحاسبة الجبر
مع تقدمك في تعلم الجبر وحساب التفاضل والتكامل, ربما تكون قد أدركت ذلك ببطء حlmadahadlat تلعب دورا حاسما. وكلما تعلمت المزيد, أدركت أنه في بعض الأحيان تكون لدينا معلومات أقل وينتهي بنا الأمر بمواجهة مشكلة حل عدم المساواة .
في جوهر الأمر, حل المتباينات ليس أصعب من حل المعادلات, بل يتطلب بضع خطوات أكثر تنظيمًا. المشكلة الرئيسية هي أننا لا نستطيع حقًا حل معظم المعادلات, على الأقل بشكل دقيق.
وحتى إذا حللنا المعادلات عدديًا, فليس لدينا طرق جيدة حتى الآن للتأكد من أننا وجدنا جميع الحلول لجميع المعادلات الممكنة. بعض المعادلات الرائعة التي يمكن حلها وتظهر في التطبيقات طوال الوقت هي الماعد , والتي يمكنك حلها باستخدام الطرق القياسية في الغالب (ولكن فقط لمتعددات الحدود ذات الدرجة الأدنى)
أحد أكثر أنواع المتباينات شيوعًا والتي تحتاج إلى حلها في اختبارات الرياضيات هي المتباينات العقلانية, لأنها أصعب المتباينات البسيطة التي يمكنك ضمان إيجاد حل لها (شريطة أن تكون الدرجات المعنية منخفضة بدرجة كافية, أو كثيرات الحدود بسيطة بما فيه الكفاية).






