关于三角导数的更多信息

使用此计算器求三角导数,在本例中,我们假设三角导数是任何有效的可微函数,包含一个或多个初等三角函数。

此计算器的一个有效函数示例是 f(x) = sin(x)/x,或 f(x) = x*sin(x^3),仅举一例。

然后,当您已经输入了相应的函数后,您就可以点击"计算"按钮,以便获得显示给您的导数计算的所有步骤。

三角函数在微积分中起着至关重要的作用,在 计算导数 一般来说。最终,更复杂的函数可以将它们的导数简化为计算更简单的三角函数的导数。

基本三角导数

使用导数规则的思想是分解一个复杂的函数,并通过使用已知函数的导数来区分它。具体来说,正弦,余弦,正切和余切等简单的三角函数将在其中发挥重要作用。

什么是基本三角导数？

• 三角导数 1： \(\frac{d}{dx} \sin (x) = \cos(x)\)
• 三角导数 2： \(\frac{d}{dx} \cos (x) = -\sin(x)\)
• 三角导数 3： \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
• 三角导数 4： \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
• 三角导数 5： \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
• 三角导数 6： \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

这些是您需要非常了解并可能记住才能使用的基本导数 衍生品规则 计算更复杂的导数

三角导数是度数吗？

不,三角函数的导数在 曲率程度 ,因此找到的三角导数反映了参数 x 以弧度测量的事实。

因此,例如,假设我们想计算 sin 的导数 学位 ,因此我们定义了 \(f(y) = \sin(y)\),其中 \(y\) 以度为单位。

现在,令 \(x = \frac{\pi y}{180}\) 为以弧度表示的等效角度,同时求解 \(y\) 我们发现 \(y = \frac{180 x}{\pi}\),然后使用链式法则：

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

因此基于此,以度为单位的正弦导数实际上是以度为单位的余弦,但乘以一个因数 \(\frac{180}{\pi}\)。

你如何求三角函数中的导数？

三角导数是根据定义找到的,使用基本的三角恒等式。例如,使用 求和公式的正弦 我们可以使用极限的定义导出 \(\sin(x)\) 的导数：

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

技巧和窍门

给你的主要收获是总是提醒你 6个三角导数是 ,并牢记它们,因为您将不断使用它们,连同基本的 区分规则 .

同样,您可以使用三角恒等式和反函数的定义来找到最常见的反三角导数。

示例：三角导数计算

考虑以下函数：\(f(x) = \sin^2(x)+ \frac{1}{x}\)。求其导数

解决方案： 三角导数涉及需要微分的三角函数。考虑函数 \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\),它包含一个正弦函数,因此它可以作为三角导数。

结果 ：对于这个例子,发现导数是：

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

在图形上描述函数及其导数非常有用。见下文：

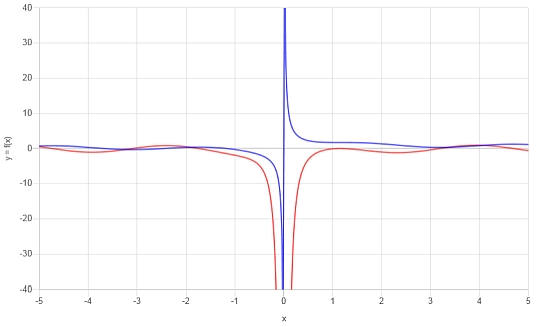
三角函数的导数示例

考虑以下三角函数：\(f(x) = \sin(x) + x \cos(x)\),求其导数。

解决方案： 现在,我们需要使用以下三角函数 \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\) 的导数。

最后的结论 ：我们得出结论,导数由下式给出：

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

得到以下图：

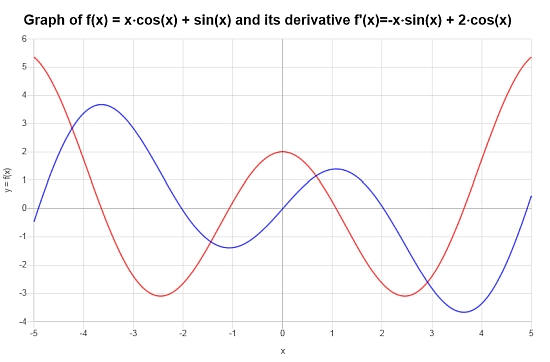
示例：三角导数和隐式微分

为 \( \sin(x)+\cos(y) = 1 \) 查找 \(\frac{dy}{dx}\)。

解决方案： 我们需要使用 隐性分化 , 所以我们区分双方并使用 链条规则 ：

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

计算结束。

其他有用的衍生计算器

寻找导数 简单和初等函数的求导是通过使用众所周知的 差异化规则 .

在这种情况下,基本 三角函数 可以被认为是初等函数,其导数可以通过其定义使用极限来计算。在我们拥有的最有用的基本函数中 多项式 和有理函数。