Обратные триггерные производные

С помощью этого калькулятора вы сможете вычислять производные обратных триггерных функций, показывая все этапы процесса.

Идея состоит в том, что предоставленная вами функция содержит обратную триггерную функцию, например, f(x) = x^2/arctan(x+1), просто для примера.

Когда вы будете готовы и закончите вводить функцию, которую нужно дифференцировать, нажмите кнопку "Рассчитать", чтобы увидеть все этапы процесса и расчетов.

Идея расчет производных обратных триггерных функций является естественным, и в следующих абзацах мы увидим, что они могут быть непосредственно выведены из триггерные производные то, что ты знаешь.

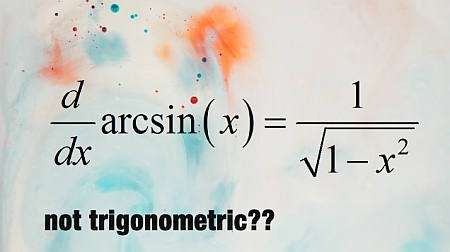
Обратные триггерные функции

Говоря простым языком, обратные триггерные функции — это те функции, которые при вычислении их на соответствующей триггерной функции приводят к тождеству. Например, если мы рассмотрим функцию \(\sin(x)\), ее обратной функцией будет \(\arcsin(x)\), и эта обратная функция обладает тем свойством, что

\[\sin(\arcsin(x)) = x \]

так же как

\[\arcsin(\sin(x)) = x \]

для всех \(x\) на определенном интервале. Строго говоря, \(\arcsin(x)\) является обратной функцией \(\sin(x)\) с алгебраической точки зрения. И то же самое касается других обратных триггерных функций и соответствующих им триггерных функций.

Расчет обратных триггерных производных

Итак, если \(f\) — функция, и у нее есть обратная \(f^{-1}\), то мы имеем это

\[f^{-1}(f(x)) = x\]

для всех \(x\). Тогда, если мы продифференцируем обе части равенства и воспользуемся цепным правилом в левой части, мы получим

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

Теперь, если мы установим \(y = f(x)\), то \(x = f^{-1}(y)\), что приведет к

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

Как мы используем это для обратных триггерных функций? Предположим, что \(f(x) = \sin(x)\) и \(f^{-1}(x) = \arcsin(x)\). Тогда, согласно общему соотношению между производной функции и производной обратной ей, получаем

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

Но изящный геометрический трюк говорит нам, что

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

что подразумевает, что

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

Остальные производные обратных триггеров получаются аналогичным образом.

Каковы 6 основных обратных триггерных функций?

• №1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
• №2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
• №3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
• №4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
• № 5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
• № 6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

Интересно, что при вычислении производной обратных тригонометрических функций ни одна из обратных тригонометрических производных не включает ни тригонометрические функции, ни обратные тригонометрические функции.

Приложения производной обратных тригонометрических функций

Триггерные функции и их производные, а также обратные триггерные функции и их производные составляют часть набора базовых функций и операций, используемых в качестве строительных блоков для создания более сложных функций.

Хотя тригонометрические функции будут появляться в приложениях чаще, чем обратные тригонометрические функции, последние также занимают видное место в исчислении, особенно при дифференцировании и использовании метода разложения на неполные дроби.

Советы и рекомендации

Не забывайте, что производные обратных тригонометрических функций могут быть чрезвычайно полезными, особенно при интегрировании членов с квадратичным знаменателем.

Кроме того, легко ошибиться при вычислении обратных триггерных производных по определению, вы определенно можете извлечь выгоду из использования производный калькулятор который покажет шаги или который вы можете использовать для проверки своей работы.

Пример: обратные триггерные производные

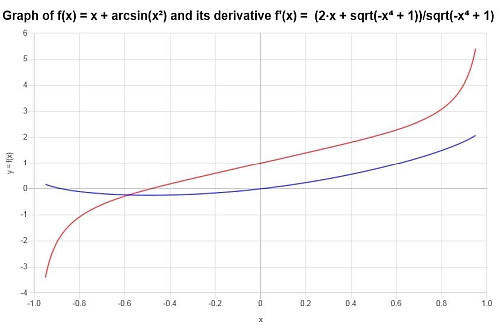
Вычислите производную от: \(f(x) = x + \arcsin(x^2)\)

Отвечать: В этом первом примере мы проанализируем \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\). Эта функция включает обратную триггерную функцию в сочетании с другой функцией. Вычислим его производную:

Отвечать : Мы можем сделать вывод, что производная функции:

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

Мы можем видеть как функцию, так и ее производную на следующем графике:

Пример: больше обратных триггерных производных

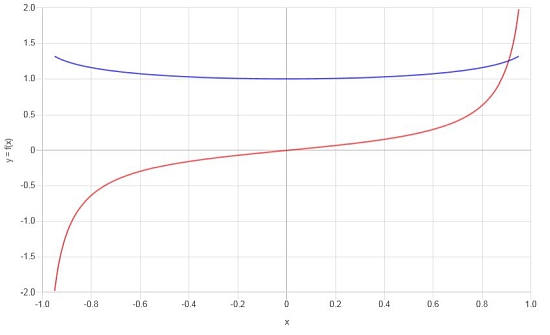
Рассмотрим следующую функцию: \(f(x) = \frac{\arcsin(x)}{x}\), вычислить ее производную.

Отвечать: Теперь для второго примера у нас есть функция \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

Окончательное Заключение : Искомая производная:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

Графически имеем следующее:

Пример обратных триггерных производных

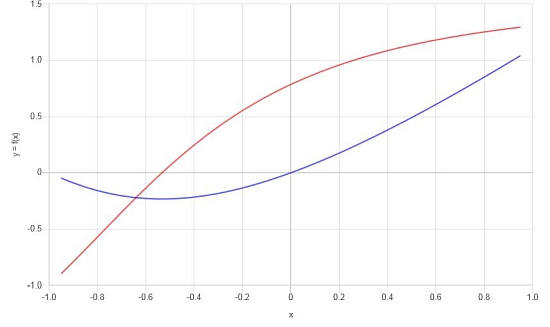
Вычислите производную от: \(f(x) = x \arctan(x+1)\)

Отвечать: Теперь в этом последнем примере мы будем работать с функцией \(\displaystyle f(x)=x\arctan\left(x+1\right)\), которая содержит обратную функцию.

Вывод : После упрощения производная равна:

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

По найденным результатам можно построить следующий график для f и f':

Другие калькуляторы исчисления

Когда используешь триггерные производные , мы заявили, что они являются важными строительными блоками для применения основных Правила производных .

Производные для обратных триггерных функций могут быть получены просто из Деривативы основных триггерных производных, и поэтому мы также рассматриваем их в группе основных производных для изучения или даже запоминания.