Подробнее о модели log-log

Этот калькулятор позволит вам рассчитать модель регрессии log-log для предоставленных вами данных. Эти данные должны быть подходящим отражением модели log-log, в которой должна быть разумная линейная степень ассоциации между ln(X) и ln(Y).

После того, как вы предоставите действительные данные, что в данном случае означает положительные данные для X и Y, вам нужно будет нажать кнопку "Рассчитать", чтобы начать работу и увидеть все этапы процесса.

Модель двойного логарифма имеет большое практическое применение, особенно в сфере экономики, где она используется для вычислить эластичности .

Что такое логарифмическая модель?

Модель логарифмического логарифма, как можно предположить из названия, представляет собой модель, в которой \(\ln(X)\) демонстрирует значительную степень линейной ассоциации с \(\ln(Y)\). Исходя из этого факта, если становится уместным рассчитать регрессионную модель для этих преобразованных данных мы ищем коэффициенты регрессии \(a\) и \(b\) для оценки

\[\displaystyle \ln(Y) = a + b \ln(X)\]

Итак, калькулятор модели двойного логарифма сводится к расчету обычной регрессионной модели для преобразованных данных \(\ln(X)\) и \(\ln(Y)\).

Шаги для оценки логарифмической модели

• Шаг 1: Четко определите переменные X и Y. Убедитесь, что они имеют одинаковый размер выборки и ОБА положительны, в противном случае вы не сможете запустить логарифмическую модель
• Шаг 2: Преобразуем исходные данные X и Y во вспомогательные ln(X) и ln(x)
• Шаг 3: Используйте обычное уравнение регрессионной модели, где вы вычисляете наклон и Y-перехват для ваших логарифмически преобразованных данных ln(X) и ln(Y)

После того, как вы оценили соответствующие коэффициенты регрессии, вы можете записать уравнение \(\displaystyle \ln(Y) = a + b \ln(X)\), которое вы можете либо оставить как есть, либо преобразовать его следующим образом:

\[\displaystyle Y = e^a \cdot x^b \]

Интерпретация логарифмической модели

Как мы можем интерпретировать найденные коэффициенты таким же образом, как мы это сделали с обычной регрессией с точки зрения предельного изменения? Для типичной задачи регрессии у вас есть коэффициент наклона, который можно интерпретировать как среднее увеличение переменной Y при увеличении переменной X на одну единицу.

В логарифмической модели это работает не совсем так, но имеет похожую предельную интерпретацию. Фактически, в модели \(\displaystyle \ln(Y) = a + b \ln(X)\) мы можем интерпретировать это следующим образом:

Увеличение X на 1% приводит к среднему увеличению Y на b% . Естественно, если \(b\), это соответствует уменьшению.

Почему мы используем этот тип модели

Одна очень веская причина в том, что она имеет сильное применение в экономике. Идея о том, что ценовая эластичность спроса просто находится путем вычисления коэффициента наклона логарифмической модели, делает ее достаточно релевантной, чтобы рассмотреть ее.

Кроме того, идея относительного предельного изменения имеет множество других применений в теории полезности в экономике, что делает ее чрезвычайно практичной и применимой моделью.

Пример расчета логарифмической регрессии

Рассмотрим следующие данные для X и Y:

Х: 1, 2, 3, 4, 5, 6, 7

Д: 10, 11,1, 13, 15,6, 16,8, 20, 22,4

Оцените соответствующую модель в логарифмическом масштабе и представьте подходящую диаграмму рассеяния

Решение:

чем завершается расчет.

Дополнительные калькуляторы регрессии

Вам нужно будет оценить, есть ли у вас значительный коэффициент корреляции между ln(X) и ln(Y) перед запуском модели. Также хорошей идеей будет построить диаграмму рассеяния данных, чтобы увидеть, соответствуют ли они тому, что ожидается от логарифмической связи.

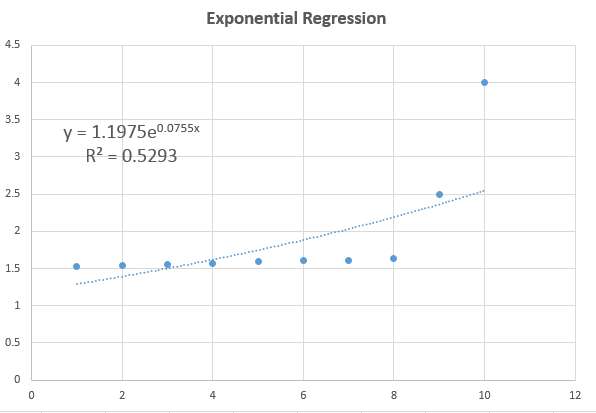
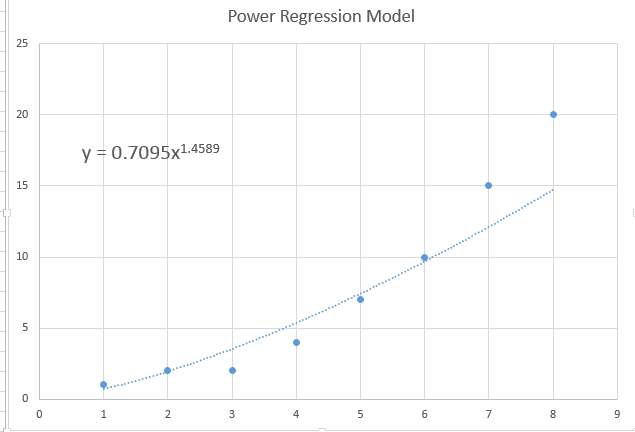
Зачастую наблюдается лишь незначительный уровень кривизны, и данные будут показывать почти плоскую картину, что также согласуется с традиционной регрессионной моделью, но это также может быть модель регрессии мощности с очень малыми коэффициентами..