Использование правила знаков декарта

Этот калькулятор поможет вам применить правило знаков Декарта для любого заданного полинома, который вы предоставите. Единственное требование к нему - полином должен быть действительным.

Например, вы можете предоставить простой кубический многочлен типа x^3 - 2x + 1, но вы можете предоставить и более сложный, например, x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1 и т.д.

Как только вы предоставите действительный полиномиальная функция вы нажимаете на кнопку "Рассчитать", чтобы все этапы процесса были показаны.

Нахождение нулей полинома является одной из самых важных задач алгебры, но в целом это непростая задача. Не существует общих формул для всех многочленов всех степеней, поэтому обычно приходится следовать систематической процедуре, чтобы найти как можно больше корней.

В этом контексте иметь как можно больше информации о типе корней всегда полезно, и это одна из целей правила знаков Декарта.

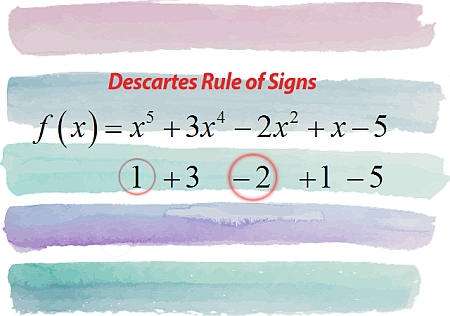
Что гласит правило знаков декарта?

Проще говоря, правило знаков Декарта говорит вам о количестве положительных и отрицательных корней многочлена, просто посмотрев на знаки коэффициентов данного многочлена.

Точнее, вы начинаете с ведущего коэффициента, игнорируете нулевые коэффициенты и продолжаете считать изменения знака. Общее число изменений знака последовательных коэффициентов является верхней границей для числа положительных корней \(p(x)\), и количество положительных корней имеет ту же четность, что и общее число изменений знаков.

Затем проделайте то же упражнение, но для коэффициентов \(p(-x)\), и в этом случае вы получите, что общее количество изменений знака последовательных коэффициентов является верхней границей для количества отрицательных корней \(p(x)\), и количество отрицательных корней имеет ту же четность, что и общее число изменений знака.

Шаги для применения правила знаков декарта

• Шаг 1: Определите многочлен p(x), который вам нужно проанализировать. Убедитесь, что это многочлен (иначе метод не сработает), и упростите его насколько возможно
• Шаг 2: Поставьте коэффициенты p(x) в ряд, начиная с ведущего коэффициента, в порядке убывания и опуская нулевые коэффициенты
• Шаг 3: Начиная с ведущего коэффициента, подсчитайте изменения знака между последовательными коэффициентами, запишите общее количество изменений знака и назовите его T
• Шаг 4: Число положительных нулей p(x) не более T и имеет ту же четность, что и T (если T четное, то число положительных нулей p(x) - четное число, а если T нечетное, то число положительных нулей p(x) - нечетное число)
• Шаг 4: Повторите тот же процесс теперь для коэффициентов p(-x), чтобы получить информацию о количестве отрицательных нулей p(x)

Этот метод может дать вам потенциально диапазон возможных значений для количества положительных (и отрицательных) нулей, но он также может потенциально сказать вам ТОЧНО, сколько положительных (или отрицательных) нулей имеет данный многочлен, в зависимости только от того, сколько изменений знака вы считаете.

Могу ли я вычислить фактические нули с помощью этого метода?

Нет, правило знаков Декарта не предназначено для того, чтобы дать вам информацию о том, каковы на самом деле корни, оно лишь говорит вам кое-что о ЧИСЛЕ положительных (и отрицательных) корней.

Теперь, объединив эту информацию с теорема о рациональном корне и другие элементарные инструменты, включая Синтетическое подразделение и теорема факторов вы будете лучше подготовлены к рассмотрению фактической стоимости корней.

Советы и рекомендации

Всегда упростить полинома. Например, если у вас есть \(p(x) = x^5 - x^3\), вы захотите сначала перейти к \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\), чтобы потом узнать, что 0 является корнем (с кратностью 3), и применить правило Декарта к \(x^2 - 1\) вместо этого.

Пример: правило знаков декарта

Укажите возможное количество положительных и отрицательных корней из \(x^4 - x^3 + x^2 + 1\)

Отвечать: Нам дана следующая полиномиальная функция: \(\displaystyle x^4 - x^3 + x^2 + 1\), для которой нам необходимо применить правило знаков Декарта.

Позитивные Корни : Коэффициенты полинома (от большей мощности к меньшей):

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

Находим, что количество изменений знака в последовательных коэффициентах составляет: \(2\), а изменениями являются: \(\,\,+1\,\,\) и\(\,\,-1\,\,\), \(\,\,-1\,\,\) и\(\,\,+1\,\,\).

Отрицательные Корни : Коэффициенты полинома для \(p(-x) = x^4+x^3+x^2+1\) составляют:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

Для коэффициентов \(p(-x)\) изменения знака не обнаружено.

Заключение: Исходя из количества найденных изменений знака, которое равно \(2\), делаем вывод, что \(p(x)\) может иметь 0 или 2 положительных корня для \(p(x) = x^4-x^3+x^2+1\).

Теперь, поскольку для коэффициентов \(p(-x)\) не было найдено изменений знака, мы заключаем, что для \(p(x) = x^4-x^3+x^2+1\) НЕТ отрицательных нулей.

Пример: еще о правиле знаков декарта

Укажите возможное количество положительных и отрицательных корней из \(x^4 + x^3 + x^2 - 1\)

Отвечать: Теперь нам нужно проанализировать \(\displaystyle x^4 + x^3 + x^2 - 1\), используя правило знаков Декарта.

Представленное выражение уже упрощено, поэтому упрощать больше нечего.

Позитивные Корни : Коэффициенты:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Обратите внимание, что количество смен знака в последовательных коэффициентах в этом случае равно \(1\), а сменами являются: \(\,\,+1\,\,\) и \(\,\,-1\,\,\).

Отрицательные Корни : Коэффициенты полинома, связанные с \(p(-x) = x^4-x^3+x^2-1\), являются:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Затем, количество изменений знака в последовательных коэффициентах равно \(3\), а изменениями являются: \(\,\,+1\,\,\) и \(\,\,-1\,\,\), \(\,\,-1\,\,\) и \(\,\,+1\,\,\), \(\,\,+1\,\,\) и \(\,\,-1\,\,\)

Заключение: Поскольку среди коэффициентов \(p(x)\) есть одна смена знака, мы заключаем, что для \(p(x) = x^4+x^3+x^2-1\) существует ровно ОДИН положительный ноль.

Исходя из количества найденных изменений знака, которое равно \(3\), делаем вывод, что \(p(x) = x^4+x^3+x^2-1\) может иметь 1 или 3 отрицательных корня.

Пример: положительные и отрицательные знаки

Укажите возможное количество положительных и отрицательных корней из \(x^4 + 1\). Можете ли вы назвать точное количество положительных и отрицательных корней?

Отвечать: В этом случае знак не меняется, поэтому положительных корней нет. Теперь \(p(-x) = (-x)^4 + 1 = x^4 + 1\), у которого нет перемены знака, поэтому отрицательных корней тоже нет. Вывод: многочлен не имеет вещественных корней (так как 0 тоже не является корнем).

Больше калькуляторов полиномов

Нахождение корней многочлена является одним из центральных пунктов большинства прикладных задач по исчислению и алгебре, и это навык, которым стоит овладеть.

В вычислении нулей многочлена участвует множество навыков, и Правило Знаков Декарта дает вам много информации, которую можно получить, просто взглянув на коэффициенты полинома.