Подробнее о графике обратных функций

Этот калькулятор поможет вам найти график предоставленной вами обратной функции при условии, что функция имеет обратную, что не всегда так.

Вы можете предоставить функцию в формате "y = 2x - 1" или просто указать выражение типа "f(x) = (x-1)/(x-3)" или просто "(x-1)/( x-3)', чтобы указать функцию.

После того, как вы предоставите действительную функцию, вы можете нажать кнопку "Рассчитать", и вам будут предоставлены все шаги расчет обратной функции , и если обратная существует, то будет показан график с функцией и обратной..

Обратите внимание, что для того, чтобы данная функция имела обратную функцию, функция должна быть взаимно однозначной, а это означает, что каждое значение в диапазоне функции имеет не более одного прообраза в области определения функции. и ровно одним прообразом мы ограничиваем эффективную дальность.

Как узнать, обратима ли функция

Прежде чем получить график обратной функции для заданной функции, необходимо знать, имеет ли эта функция вообще обратную функцию. Основным критерием инверсии является соотношение "один к одному", что означает, что одно значение в диапазоне не может иметь два связанных значения (прообраза).

Возможно, студенты предпочитают не использовать технические термины, такие как "образы" и "прообразы", и хотя это основные понятия теории функций, в этом случае мы можем использовать простой графический тест, чтобы оценить, является ли функция однозначной. один, и, следовательно, если вы сможете найти и построить график его обратного значения.

Тест горизонтальной линии

Тест горизонтальной линии показывает, что для того, чтобы функция была взаимно однозначной, любая построенная вами горизонтальная линия пересекает график функции не более одного раза. Если вам удалось найти одну горизонтальную линию, которая пересекает график данной функции более одного раза, то функция НЕ является однозначно однозначной.

Например, показанная ниже функция является взаимно однозначной, поскольку какую бы горизонтальную линию мы в нее ни кинули, она пересечет график функции ровно один раз:

Но тогда в следующем примере показана функция, которая не является взаимно однозначной, потому что мы видим горизонтальную линию, которая пересекает линию функции 2 раза (более одного раза):

Шаги по поиску обратного графа

• Шаг 1: Существует два распространенных метода: графический и аналитический
• Шаг 2: Для графического метода вам необходимо сначала применить тест горизонтальной линии и убедиться, что он проходит его, поэтому он является взаимно однозначным и существует обратный вариант
• Шаг 3: Затем вы рисуете на графике линию y = x (прямая линия с углом 45°) ^О градусы относительно оси x
• Шаг 4: После этого вы просто используете линию y = x как "зеркало" и отражаете точки исходного графика относительно "зеркала". Полученный граф с помощью этого процесса зеркалирования является графиком обратной
• Шаг 5: Для аналитического метода нужно сначала алгебраически найти обратное : вы начинаете с y = f(x), а затем находите y.
• Шаг 6: Если существует только одно решение, то существует обратное, и вы пишете его x = g(y). Корректируя имена переменных, вы формально определяете обратную функцию \(f^{-1}\) в терминах g
• Шаг 7: Наконец, вы строите график найденного обратного \(f^{-1}\), как обычно построить график функции обычно

Когда вам нужно найти график, обратный, как графический, так и аналитический методы подходят, только аналитический метод имеет преимущество, заключающееся в том, что вы вычисляете обратную функцию в процессе процесса, поэтому в конечном итоге у вас есть ее математическое выражение. не только его график.

Зачем вам график обратного

Есть так много причин, по которым вы бы это сделали. Во-первых, обратная функция сама по себе является очень важным действующим лицом в теории функций, поскольку функция показывает, как перейти от x к ay, поэтому вполне естественно захотеть узнать, каков механизм перехода от y к x, и именно это и дает вам обратная функция.

Таким образом, можно представить функцию как одностороннюю карту от точки "X" к точке "Y", а вычисление обратной функции похоже на явное определение карты для перехода от "Y" к "X".

И тогда график обратной функции расскажет вам много информации об этой обратной функции: снижается ли она вверх, как она себя ведет.

Как мне поможет этот калькулятор обратного графика?

Сначала этот калькулятор проанализирует функцию, чтобы определить, является ли она обратимой, используя аналитический метод, и, если возможно найти такую обратную функцию, он построит ее график.

Нахождение обратного предполагает решение уравнения , что является непростой задачей, если вы не имеете дело с Линейные уравнения или полиномиальные уравнения , но в остальном процесс может быть очень сложным или даже невозможным.

Другие калькуляторы могут выполнять аналогичный процесс, но одно из преимуществ этот калькулятор заключается в том, что в нем представлены все этапы процесса с подробным объяснением, где это возможно.

Пример: нахождение графика обратного

Постройте график, обратный : \( y = \frac{2}{3} x - \frac{5}{6}\)

Решение:

Нам была предоставлена следующая функция:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Затем, чтобы найти обратную заданную функцию, нам нужно найти \(x\) и определить, существует решение или нет. Исходное уравнение:

\[y=\frac{2}{3}x-\frac{5}{6}\]

Шаг 0: В этом случае нам сначала необходимо упростить данное линейное уравнение, и для этого мы проводим следующие шаги упрощения:

Решение линейного уравнения

Поместив \(x\) слева и \(y\) и константу справа, мы получим

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Теперь, решая \(x\), разделив обе части уравнения на \(-\frac{2}{3}\), получаем следующее:

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

и упрощая окончательно получаем следующее

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Следовательно, решение \(y\) для данного линейного уравнения приводит к \(x = \frac{3}{2}y+\frac{5}{4}\).

Следовательно, и поскольку при решении \(x\) мы находим решение, и это только одно решение, мы нашли обратное.

Найдена обратная функция

На основании показанной выше работы можно сделать вывод, что обратная функция имеет вид:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

Обратная функция может быть изображена графически следующим образом:

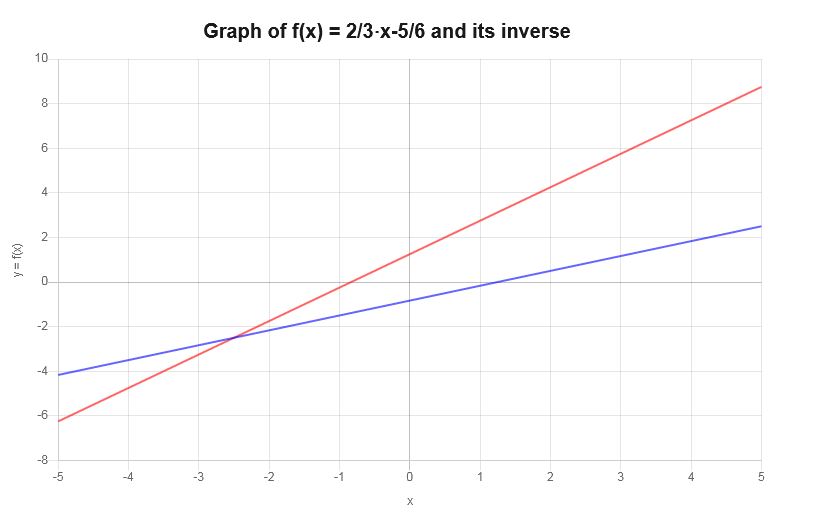
Пример: больше обратных графиков

Можете ли вы найти обратный график: \(y = x^2\)?

Решение: Нет, мы не можем найти обратный график \(y = x^2\), поскольку эта функция не проходит тест на горизонтальную линию. Другой способ увидеть это состоит в том, что при решении \(x\) мы получаем \(x = \pm \sqrt y\), а поскольку мы находим два решения, то обратного решения нет, и, следовательно, нет обратного графа.

Другие калькуляторы функций

Функции и любые типы функциональных операций действительно являются центром алгебры и исчисления. Хороший Функциональный калькулятор облегчит вашу жизнь с точки зрения сведения функции к ее простейшему выражению.

Тогда у вас будет хорошее инструмент для построения графиков функций чтобы быстро взглянуть на графические свойства функции. Вид графика функции может многое рассказать о ее поведении даже до того, как вы посмотрите на ее алгебраическое выражение.

Затем у вас есть более сложные операции, такие как поиск производной, для которых это Калькулятор дифференцирования пригодится, так как покажет вам все этапы процесса. Как и ожидалось, производная обратной функции имеет интересную связь с производной исходной функции.