Об этом графе неравенств

Этот калькулятор поможет вам найти решение и график любого общего неравенства с указанием всех шагов. Вам необходимо указать допустимое неравенство одной переменной (x), введя его в соответствующее поле.

Например, вы можете указать простое линейное неравенство, например "3x – 1 < 1/3" или что-то вроде "2x-x^2 <= 3/4", что соответствует квадратному неравенству.

После того, как вы предоставили неравенство, которое хотите отобразить на графике, нажмите кнопку "Решить", чтобы получить решения со всеми шагами на случай, если можно было найти решения.

Решение общих уравнений и всеобщее неравенство в целом представляет собой трудную задачу, за исключением определенного набора структур, поддающихся систематическому рассмотрению.

Некоторые из немногих типов, которые допускают точное решение: линейные неравенства и полиномиальные неравенства .

Важный тип неравенства, который вам захочется решить, — это рациональные неравенства, в которых вы можете определить частное многочленов. Эти неравенства интересны тем, что у них есть потенциальное деление на ноль, с которым необходимо разобраться. Идею рационального неравенства можно легко распространить на частное функций вообще, не обязательно полиномов

Как построить график неравенства

Самый простой ответ на него: чтобы построить график неравенства, нужно знать, как его решать. Графическое решение неравенства обычно представляется в виде интервала или нескольких соединенных интервалов по оси x.

Итак, с учетом вышесказанного, построение графика неравенства начинается с его решения, которое включает в себя поиск набора значений на реальной линии, которые удовлетворяют указанному неравенству.

Потенциально вы можете представить график как отдельный интервал или построить решения неравенства вместе с графиком выражения, лежащего в основе неравенства: напомним, что для того, чтобы решать неравенства , вы передаете все члены в одну сторону (что дает вам основное выражение) и решаете вспомогательное уравнение

Шаги по решению и построению графиков неравенств

• Шаг 1: Передайте все члены в одну сторону, чтобы с одной стороны у вас было одно выражение, а с другой — ноль
• Шаг 2: Из неравенства (раз уж с одной стороны всё, а с другой ноль) постройте вспомогательное уравнение
• Шаг 3: Решите это уравнение методом, подходящим для его структуры (для разных типов уравнений потребуются определенные методы и подходы)
• Шаг 4: На основе РЕАЛЬНЫХ решений вспомогательных уравнений (действительных, а не комплексных решений) вы строите критические точки и сортируете их в порядке возрастания
• Шаг 5: Вам также нужно искать точки, где выражение не определено. Один примечательный случай этого происходит с рациональными неравенствами, в которых знаменатель является многочленом, поэтому выражение будет неопределенным в нулях знаменателя. Таким образом, вы добавляете нули знаменателя в список критических точек
• Шаг 6: Используя критические точки, вы строите интервалы, используя последовательные критические точки (используя -∞ и ∞ в качестве начальной и конечной критических точек)
• Шаг 7: Для каждого интервала проанализируйте знак выражения и посмотрите, совместим ли он со знаком неравенства. Если да, то интервал будет частью общего решения неравенства

Использование критических точек для анализа имеет первостепенное значение, поскольку таким образом вы уверены, что выражение не меняет знак внутри каждого интервала, и проблема сводится к оценке того, решено ли неравенство для каждого из этих критических интервалов.

Чтобы сделать это более ощутимым, вам задано некоторое неравенство, а затем вы передадите все в одну сторону, и у вас получится что-то вроде \(f(x) \le 0\). Например, это может быть что-то вроде \(x^2 - x + 1 \le 0\).

Итак, вы берете \(f(x) \le 0\) и находите вспомогательное уравнение \(f(x) = 0\). Вы берете выражение \(f(x)\) и находите его нули критическими точками. Но вы не только это сделаете, но и посмотрите, не определен ли где-нибудь \(f(x)\) (деление на ноль и т. д.). Оно может быть определено везде, как в случае \(x^2 - x + 1\), но если вы обнаружите точки, в которых выражение не определено, вы добавите его в список критических точек.

Затем вы строите интервалы на основе последовательных критических точек. Для \(f(x) \le 0\) в состав решений вы возьмете те интервалы, где значение выражения отрицательно. Если исходное неравенство было бы \(f(x) \ge 0\), вы возьмете в качестве части решения те интервалы, где значение выражения положительное

Как работает этот графический редактор неравенства

Наш онлайн-график неравенства позаботится об одном из самых громоздких процессов в базовой алгебре, который связан с поиском решений неравенства и их построением в виде графика. Большим преимуществом нашего калькулятора является то, что он показывает все шаги, когда это возможно.

Сначала графист решит неравенство, сначала решив подходящее вспомогательное уравнение. Этот процесс требует обнаружения конкретных известных структур, поскольку все структуры, вероятно, требуют разных подходов. Например, чтобы решить рациональное неравенство (которое включает в себя частное двух полиномов), например

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

вам потребуется другой подход, чем тот, который используется, например, для решения квадратного неравенства, такого как \(x^2 + 3x < 1\), и этот калькулятор учтет все эти детали

Если традиционная или общеизвестная структура не обнаружена, будут использоваться другие часто используемые замены, такие как, например, \(u = \sqrt x\) или \(u = \sin x\). Если ничего не помогает, калькулятор попытается найти решения путем проверки и численного анализа, чтобы получить хотя бы представление о решениях.

Как представить график неравенства?

Как мы упоминали выше, на самом деле это не написано на камне, но наиболее распространенный способ — построить график основного выражения неравенства и выделить значения x, которые удовлетворяют неравенству. Это, возможно, лучший графический формат для этого, и именно он используется в этом графическом редакторе.

Вы также можете нарисовать отдельный интервальный объект, но это, возможно, менее показательно, поскольку он теряет представление о том, что на самом деле происходит с самим неравенством.

Пример: графическое отображение неравенств

Постройте график следующего неравенства: \(\frac{1}{x}+x > 1\)

Отвечать: Нам дано следующее неравенство, которое необходимо решить:

\[\frac{1}{x}+x > 1\]

Нам нужно сложить все члены неравенства в одну сторону:

\[x+\frac{1}{x}-1>0\]

Решение вспомогательного уравнения

Из приведенного выше неравенства мы получаем связанное уравнение, которое необходимо решить в первую очередь:

\[x+\frac{1}{x}-1=0\]

Анализ критических точек

Нам нужно организовать найденные критические точки (из вещественных корней числителя и знаменателя) в порядке возрастания, определить интервалы со всеми последовательными критическими точками и оценить знак левого размера неравенства на каждом из этих интервалов. .

Единственная обнаруженная критическая точка — это \(0\).

Исходя из этого, нам необходимо проанализировать следующие интервалы:

• Для интервала \(\left(-\infty, 0\right)\): числитель положительный, а знаменатель отрицательный, поэтому левая часть отрицательна, что означает, что \(\left(-\infty, 0\right)\) не является частью решения.

• Для интервала \(\left(0, \infty\right)\): числитель положительный, а знаменатель положительный, поэтому левая часть положительна, поэтому \(\left(0, \infty\right)\) является частью решения.

Решение неравенства

На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x > 0\).

Используя интервальную запись, решение записывается как:

\[\left(0,\infty\right)\]

С помощью графа неравенств получается следующее:

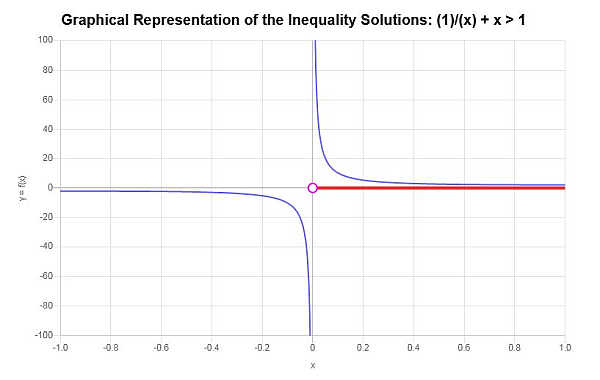
чем завершается расчет.

Пример. построение графиков полиномиальных неравенств

Найдите на графике неравенство: \(x^2 - 2x \ge 4\)

Решение:

Нам нужно сложить все члены неравенства в одну сторону:

\[x^2-2x-4\ge0\]

Решение вспомогательного уравнения

Из приведенного выше неравенства мы получаем связанное уравнение, которое необходимо решить в первую очередь:

\[x^2-2x-4=0\]

Использование квадратичной формулы

Для квадратного уравнения вида \(a x^2 + bx + c = 0\) корни вычисляются по следующей формуле:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В этом случае нам нужно решить уравнение \(\displaystyle x^2-2x-4 = 0\), что означает, что соответствующие коэффициенты:

\[a = 1\] \[b = -2\] \[c = -4\]

Сначала мы вычислим дискриминант, чтобы оценить природу корней. Дискриминант вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Поскольку в этом случае мы получаем дискриминант \(\Delta = \displaystyle 20 > 0\), который является положительным, мы знаем, что уравнение имеет два разных действительных корня.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

итак, мы выяснили, что:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

В этом случае квадратное уравнение \( \displaystyle x^2-2x-4 = 0 \) имеет два действительных корня, поэтому:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

тогда исходный полином факторизуется как \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), что завершает факторизацию.

Анализ критических точек

Список обнаруженных критических точек организован в порядке возрастания: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

Исходя из этого, нам необходимо проанализировать следующие интервалы:

• Для интервала \(\left(-\infty, -\sqrt{5}+1\right)\): левая часть положительна, поэтому \(\left(-\infty, -\sqrt{5}+1\right)\) является частью решения.

• Для интервала \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): левая часть отрицательна, поэтому \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) не является частью решения.

• Для интервала \(\left(\sqrt{5}+1, \infty\right)\): левая часть положительна, что означает, что \(\left(\sqrt{5}+1, \infty\right)\) является частью решения.

Решение неравенства

На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x \le -\sqrt{5}+1\) или \(x \ge \sqrt{5}+1\).

Используя интервальную запись, решение записывается как:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Графически:

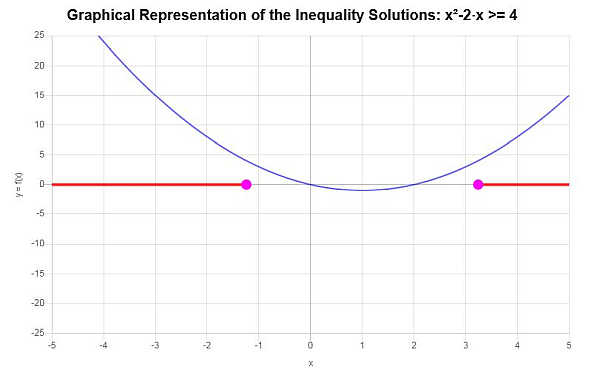
чем завершается расчет.

Больше калькуляторов по алгебре

По мере продвижения в изучении алгебры и исчисления вы, вероятно, постепенно осознали, что Решение уравнений играют решающую роль. И по мере того, как вы узнаете больше, вы понимаете, что иногда у нас меньше информации, и в конечном итоге мы сталкиваемся с проблемой Решение неравенств .

По сути, решать неравенства не сложнее, чем решать уравнения, просто требуется несколько более организованных шагов. Основная проблема в том, что мы не можем решить большинство уравнений, по крайней мере точно.

И даже при численном решении уравнений у нас пока нет хороших способов гарантировать, что мы нашли ВСЕ решения ВСЕХ возможных уравнений. Некоторые замечательные уравнения, которые можно решить и которые постоянно появляются в приложениях, — это полиномиальные уравнения , которую можно решить преимущественно стандартными методами (но только для полиномов меньшей степени)

Одним из наиболее часто задаваемых типов неравенств, которые вам нужно решить в тестах по математике, являются рациональные неравенства, поскольку они представляют собой самое сложное простое неравенство, решение которого можно как бы гарантировать (при условии, что соответствующие степени достаточно малы или полиномы достаточно просты).