इस रैखिक असमानता कैलकुलेटर के बारे में अधिक जानकारी

यह कैलकुलेटर आपको रैखिक असमानताओं से निपटने के लिए आवश्यक उपकरण प्रदान करेगा। विशेष रूप से, आप दिखाए गए सभी चरणों को प्राप्त करते हुए, उन्हें हल करने और उनका ग्राफ़ बनाने में सक्षम होंगे।

'2x + 3 < 1' या '3x + 2y <=1' जैसी रैखिक असमानताओं की अनुमति है, और फिर चर की संख्या के आधार पर, आपको समाधान की ओर ले जाने वाले चरणों के साथ एक उपयुक्त ग्राफ मिलेगा।

एक बार वैध रैखिक असमानता प्रदान कर दी गई है, तो प्रक्रिया शुरू करने के लिए आपको बस "हल करें" पर क्लिक करना होगा। अगर कुछ गलत है या छूट गया है तो कैलकुलेटर आपको इसके बारे में बता देगा।

इस प्रकार की असमानताएँ आपको सबसे सरल प्रकार की मिलेंगी, और इन्हें हल करना हमेशा अपेक्षाकृत आसान होता है। इस प्रकार साथ में द्विघात असमानताएँ हल करने योग्य एकमात्र "आसान" असमानताओं में से हैं।

रैखिक असमानता क्या है?

रैखिक असमानता असमानता का सबसे सरल प्रकार है, जिसमें शामिल सभी पद रैखिक या स्थिर होते हैं।

\[\displaystyle a x + b y \le 1\]

उदाहरण के लिए, उपरोक्त समीकरण दो चर वाला एक रैखिक समीकरण है। तकनीकी रूप से कहें तो, हमारे पास है बहुपद असमानता डिग्री 1 का, लेकिन इसे देखने का यह एक प्रकार का अत्यधिक जटिल तरीका है।

आप एक रैखिक असमानता को कैसे हल करते हैं?

• Letsunt 1: वह सब कुछ जिसमें वह वेरिएबल है जिसे आप हल करना चाहते हैं, एक तरफ रखें और बाकी को दूसरी तरफ रखें
• Their दो दो: समूह और अभिव्यक्ति को सरल बनाएं , ताकि समान पदों को कम किया जा सके
• Theirण 3: यदि एक से भिन्न कोई स्थिरांक उस चर को गुणा कर रहा है जिसे आप हल करना चाहते हैं, तो उससे भाग दें। एक चेतावनी: यदि आप ऋणात्मक मान से विभाजित करते हैं, तो आपको असमानता की दिशा बदलनी होगी

ध्यान में रखने योग्य मुख्य बिंदुओं में से एक, और जो समीकरणों और असमानताओं को हल करने की प्रक्रियाओं को अलग करता है, वह यह है कि समीकरणों को हल करते समय हम अधिक स्वतंत्र रूप से स्थिरांक से गुणा (या विभाजित) कर सकते हैं और कुछ भी नहीं बदलता है, जबकि असमानताओं के साथ हमें अधिक सावधान रहने की आवश्यकता है, क्योंकि ऋणात्मक स्थिरांकों से गुणा (या भाग) करने पर असमानता की दिशा बदल जाती है।

सबसे सामान्य रैखिक असमानता क्या है?

रैखिक के साथ आप जो सबसे सामान्य चीज़ प्राप्त कर सकते हैं वह है

\[\displaystyle a x + bx \le c\]

लेकिन फिर भी आपके पास '\(\le\)' के बजाय '<' हो सकता है। या हम कर सकते थे

\[\displaystyle a x + bx \ge c\]

लेकिन आप '\(\ge\)' के स्थान पर '>' का भी उपयोग कर सकते हैं।

इसके अलावा और घटाव के साथ क्या हुआ, विभाजन को विभाजित करना केवल अंशों के गुणन से लिया गया है: दो अंशों को विभाजित करने के लिए, आप बस पहले एक से गुणा करते हैं तंग दूसरे में से (उलटा अंश अंश में भाजक द्वारा अंश को स्वैप करके प्राप्त किया जाता है)।

अनुप्रयोग

गणित में रैखिक असमानताओं का बहुत उपयोग होता है। रैखिक असमानता एक प्रकार का भारित औसत है, जो सभी प्रकार के मिश्रण और असाइनमेंट समस्याओं के लिए बहुत उपयुक्त है।

शाब्दिक समस्याओं से निपटते समय, आमतौर पर आपको रैखिक समीकरण मिलते हैं, लेकिन रैखिक असमानताओं से भी निपटना असामान्य नहीं है।

सबसे प्रसिद्ध क्षेत्रों में से एक अनुकूलन और रैखिक प्रोग्रामिंग है, जिसमें गैर-रेखीय उद्देश्य फ़ंक्शन से निपटने के दौरान सिंप्लेक्स विधि और कुह्न-टकर स्थितियों दोनों के साथ रैखिक असमानताएं एक महत्वपूर्ण भूमिका निभाती हैं।

उदाहरण: असमानताओं को हल करना

निम्नलिखित रैखिक असमानता को हल करें: \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

समाधान:

हमें असमानता की सभी शर्तों को एक तरफ रखना होगा:

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

संबद्ध सहायक समीकरण

हमें हल करना होगा:

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Theirण 0: इस मामले में, हमें पहले दिए गए रैखिक समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

रैखिक समीकरण को हल करना

\(x\) को बायीं ओर और दायीं ओर रखने पर हमें स्थिरांक प्राप्त होता है

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(\frac{2}{3}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=-\frac{17}{8}\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(x\) को हल करने पर \(x=-\frac{17}{8}\) प्राप्त होता है।

महत्वपूर्ण बिंदु

जैसा कि रैखिक असमानता के लिए अपेक्षित है, केवल एक महत्वपूर्ण बिंदु है, जो \(-\frac{17}{8}\) है, जिससे हम निम्नलिखित अंतरालों का विश्लेषण करते हैं:

• अंतराल \(\left(-\infty, -\frac{17}{8}\right)\) के लिए: बाईं ओर नकारात्मक है, जिसका अर्थ है कि \(\left(-\infty, -\frac{17}{8}\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(-\frac{17}{8}, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(-\frac{17}{8}, \infty\right)\) समाधान का हिस्सा नहीं है।

असमानता का समाधान

इसलिए, यह पाया गया कि असमानता का समाधान है: \(x < -\frac{17}{8}\)।

अंतराल संकेतन के साथ अभिव्यक्ति समाधान, समाधान इस प्रकार लिखा गया है:

\[\left(-\infty,-\frac{17}{8}\right)\]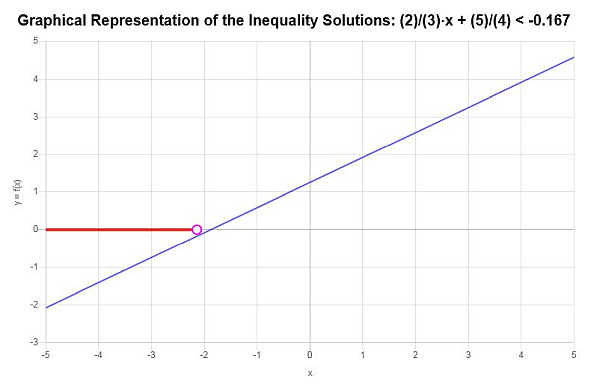

उदाहरण: अधिक रैखिक असमानताएँ

इस 2-चर रैखिक असमानता को हल करें: \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

समाधान:

हमें हल करना होगा:

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

हमारे पास एक रैखिक असमानता दी गई है, और हमें चर \(y\) को हल करने की आवश्यकता है।

इस मामले में, हम \(y\) को हल करते हैं, इसलिए इसे असमानता के एक तरफ और बाकी को दूसरी तरफ रखने पर हमें मिलता है:

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

\(y\) को हल करने के लिए, हम असमानता के दोनों पक्षों को \(\frac{5}{4}\) से विभाजित करते हैं, इसलिए हमें अंततः मिलता है:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

रैखिक असमानता समाधान

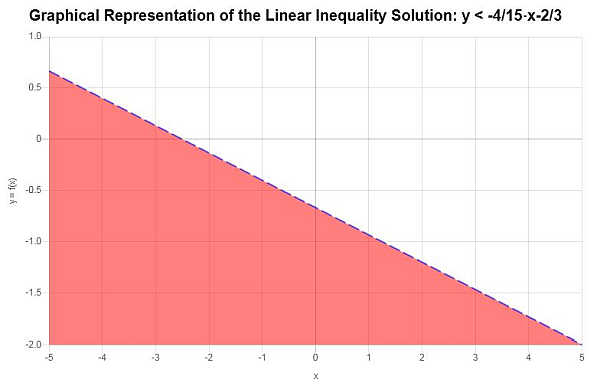
प्रदान की गई असमानता के आधार पर, इसे \(y\) के लिए हल करने के बाद हमें मिलता है:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

समाधान क्षेत्र का चित्रमय प्रतिनिधित्व नीचे दिए गए ग्राफ़ में दिखाया गया है:

अधिक बीजगणित कैलकुलेटर

बीजगणित में अभिव्यक्ति से निपटना महत्वपूर्ण है। अभिव्यक्ति सरलीकरण अधिकांश गणितीय प्रक्रियाओं की शुरुआत है, और आपको आमतौर पर चीज़ों को उसकी सरलतम अभिव्यक्ति तक सीमित करने की आवश्यकता होती है।

समीकरण हल करना और भी असमानताओं का समाधान अधिकांश प्रक्रिया के मूल में रहेगा, क्योंकि गणित में आप जो कुछ भी करते हैं उसके केंद्र में कोई न कोई रहेगा।