द्विघात असमानताओं के बारे में अधिक जानकारी

यह द्विघात असमानता गणना आपको सभी चरणों को दिखाते हुए असमानताओं का समाधान प्रदान करेगी। उदाहरण के लिए, आपके द्वारा प्रदान की गई असमानता 'x^2 - 1/2 > 0' जैसी कुछ हो सकती है, और सामान्य तौर पर, द्विघात असमानताओं को हल करना बहुत कठिन नहीं होता है।

एक बार जब आप एक वैध असमानता प्रदान करते हैं जिसमें शामिल है द्विघात अभिव्यक्ति , आप असमानता समाधान के ग्राफ़ सहित, आपको दिखाए गए गणना के सभी चरण प्राप्त करने के लिए "गणना करें" पर क्लिक कर सकते हैं।

द्विघात असमानताएँ कुछ प्रकारों में से एक हैं (साथ में)। रैखिक असमानताएँ ) कि आपको एक सटीक समाधान खोजने में सक्षम होने की गारंटी दी जाती है, और इस प्रक्रिया में एक द्विघात समीकरण को हल करना शामिल है।

इस प्रकार की असमानता की परिभाषा क्या है?

हमने इसे स्पष्ट रूप से नहीं कहा है, लेकिन यह इसके नाम से स्पष्ट हो जाता है: द्विघात असमानता एक विशिष्ट प्रकार की असमानता है जिसमें इसमें शामिल सभी पद अधिकतम 2 डिग्री के बहुपद हैं। इस संदर्भ में, एक उदाहरण है

\[\displaystyle x^2 < x - 1\]

जो इस तथ्य से द्विघात है कि असमानता के दोनों पक्ष अधिकतम 2 क्रम के बहुपद हैं। अब, यदि आपके पास:

\[\displaystyle x^2 < x^3 - 1\]

तब असमानता अब द्विघात नहीं रह गई है, क्योंकि दाहिनी ओर \(x^3\) शब्द है। इन असमानताओं का समाधान खोजने के लिए हमारे पास एक स्पष्ट रोडमैप है।

द्विघात असमानताओं को हल करने के चरण

• Letsunt 1: सुनिश्चित करें कि आपके पास द्विघात असमानता है, क्योंकि इस मामले में उपयोग की गई विधि केवल इस प्रकार की असमानता के लिए मान्य है
• Their दो दो: अधिकांश असमानताओं की तरह, असमानता के बाईं ओर सब कुछ पास करें, और संबंधित समीकरण को हल करें
• Theirण 3: यदि संबंधित द्विघात समीकरण में वास्तविक जड़ें नहीं हैं, तो हम जानते हैं कि या तो पूरी वास्तविक रेखा एक समाधान है, या कोई समाधान नहीं है। तो आप किसी भी बिंदु का परीक्षण करें और देखें कि क्या यह असमानता को हल करता है, और यदि यह करता है, तो समाधान पूरी वास्तविक रेखा (-∞, ∞) है, अन्यथा, समाधान खाली है।
• च ४: ४: यदि संबंधित द्विघात समीकरण का केवल एक ही वास्तविक समाधान है, तो इसका मतलब है कि संबंधित द्विघात ग्राफ x-अक्ष को स्पर्शरेखा से छूता है। तो असमानता चिह्न के आधार पर, आपके पास केवल स्पर्श बिंदु ही समाधान हो सकता है, या स्पर्श बिंदु को छोड़कर बाकी सब समाधान हो सकता है, या संपूर्ण वास्तविक रेखा (-∞, ∞), जिसके लिए आपको स्पर्श बिंदु का परीक्षण करने की आवश्यकता है, और उसके बाहर एक बिंदु (बिंदु के बाएँ और दाएँ)
• च ४: ४: यदि संबंधित द्विघात समीकरण के दो अलग-अलग वास्तविक समाधान हैं, तो आप यह निर्धारित करने के लिए इन जड़ों द्वारा परिभाषित अंतराल की जांच करें कि वास्तविक रेखा के कौन से हिस्से समाधान का हिस्सा होंगे

एक तो आप टुकड़ों का विश्लेषण करते हैं, यदि आवश्यक हो, तो आप "संघ" ऑपरेटर का उपयोग करके उन्हें जोड़ते हैं, जिसका उपयोग अंतरालों को एक साथ जोड़ने के लिए किया जाता है।

आप द्विघात असमानता कैसे बनाते हैं?

असमानताओं का रेखांकन समाधान कैसा दिखता है यह समझने का एक शानदार तरीका प्रदान करता है। प्रक्रिया के संदर्भ में, आपको यह जानना होगा कि क्या आप एक चर असमानता के साथ काम कर रहे हैं, या आपके पास अधिक चर हैं।

यदि आपके पास कोई असमानता है जैसे कि

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

आपके पास केवल एक चर है, और फिर समाधान वास्तविक रेखा का एक उपसमुच्चय होगा। दूसरी ओर, यदि आपके पास ऐसा कुछ है

\[\displaystyle y < x^2 - \frac{1}{2} x \]

तब आपके पास केवल दो चर x और y होंगे, और तब असमानता का समाधान xy तल का एक उपसमुच्चय होगा।

द्विघात व्यंजकों का महत्व

समीकरणों और असमानताओं में शामिल द्विघात अभिव्यक्तियाँ गणित में मौलिक भूमिका निभाती हैं। शायद, रैखिक के बाद द्विघात सबसे व्यापक रूप से उपयोग की जाने वाली संरचना है।

कैलकुलस और बीजगणित से निपटते समय आपको अधिकतमीकरण और न्यूनतमकरण, एकीकरण और बहुत कुछ की समस्याओं में द्विघात के अनगिनत अनुप्रयोग मिलेंगे। थोड़ा खोदने पर आपको विभिन्न वैज्ञानिक अनुशासनों में द्विघात अभिव्यक्तियों के अनुप्रयोग मिलेंगे

उदाहरण: द्विघात असमानताएँ

इस द्विघात असमानता को हल करें: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

समाधान:

हमें पहले निम्नलिखित सहायक द्विघात समीकरण \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\) को हल करना होगा।

द्विघात सूत्र को लागू करना

द्विघात समीकरण है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस मामले में, हमारे पास है:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

इन मानों को जड़ों के सूत्र में जोड़ने पर हमें प्राप्त होता है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

महत्वपूर्ण बिंदु

आरोही क्रम में व्यवस्थित पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\)।

फिर, हमें निम्नलिखित महत्वपूर्ण अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) के लिए: बायां पक्ष सकारात्मक है, इसलिए \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) के लिए: बाईं ओर नकारात्मक है, जिसका अर्थ है कि \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) समाधान का एक हिस्सा है।

• अंतराल \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) समाधान का हिस्सा नहीं है।

समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]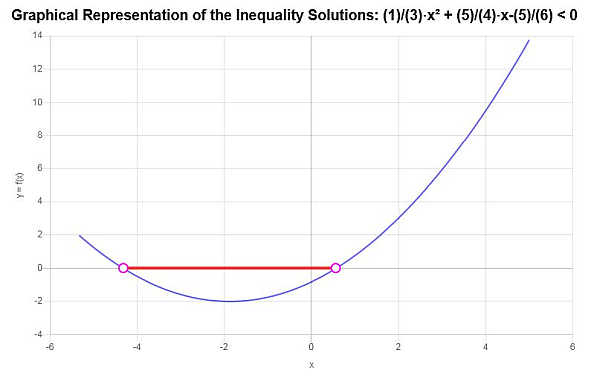

उदाहरण: अधिक द्विघात असमानताएँ

हल करें: \(x^2 < 4\)

समाधान:

दी गई असमानता है:

\[x^2 < 4\]

जो द्विघात समीकरण \(\displaystyle x^2-4=0\) से प्राप्त होता है।

द्विघात सूत्र

\(a x^2 + bx + c = 0\) रूप के द्विघात समीकरण के लिए, मूलों की गणना निम्नलिखित का उपयोग करके की जाती है तमाम :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस मामले में, हमारे पास है कि हमें जिस समीकरण को हल करने की आवश्यकता है वह \(\displaystyle x^2-4 = 0\)है, जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 1\] \[b = 0\] \[c = -4\]

सबसे पहले, हम जड़ों की प्रकृति का आकलन करने के लिए भेदभाव की गणना करेंगे।भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

चूंकि इस मामले में हमें भेदभावपूर्ण \(\Delta = \displaystyle 16 > 0\)है, जो सकारात्मक है, हम जानते हैं कि समीकरण में दो अलग -अलग वास्तविक जड़ें हैं।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

इस मामले में, द्विघात समीकरण \( \displaystyle x^2-4 = 0 \), की दो वास्तविक जड़ें हैं, इसलिए फिर:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

तो फिर मूल बहुपद \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \)के रूप में फैक्टर किया जाता है, जो कारक को पूरा करता है।

महत्वपूर्ण बिंदुओं का विश्लेषण

आरोही क्रम में व्यवस्थित पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(-2\), \(2\)।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -2\right)\) के लिए: बायां पक्ष सकारात्मक है, इसलिए \(\left(-\infty, -2\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(-2, 2\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-2, 2\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(2, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(2, \infty\right)\) समाधान का हिस्सा नहीं है।

असमानता का समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(-2< x \le 2\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left[-2,2\right)\]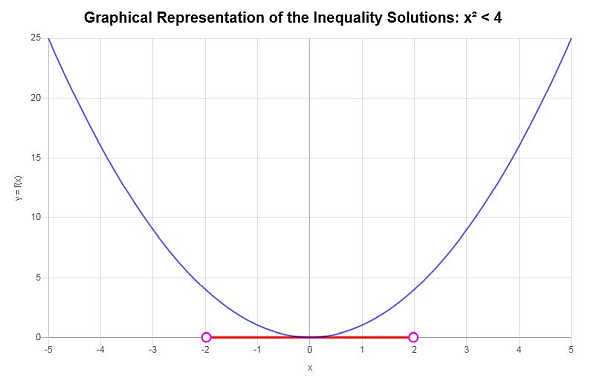

अन्य उपयोगी असमानता कैलकुलेटर

सबसे सरल असमानता प्रकार जिसे आप हल कर पाएंगे रैखिक असमानताएँ . उसके बाद, सहजता के संदर्भ में, आपके पास द्विघात असमानताएँ हैं।

फिर, आपके पास है बहुपद असमानताएँ सामान्य तौर पर, 2 से अधिक डिग्री के साथ। वे सीधे होने चाहिए, लेकिन उन्हें हल करने के लिए आवश्यक श्रमसाध्य कार्य की मात्रा के मामले में वे अभी भी कठिन कार्य हो सकते हैं।

एक होना असमानता कैलकुलेटर सामान्य तौर पर असमानताएं वास्तव में काम आ सकती हैं, क्योंकि यह विभिन्न प्रकार की असमानताओं को संबोधित करेगी जो सटीक समाधान की खोज के लिए उत्तरदायी हैं।