Индивидуальные функции
Инструкции: Используйте этот калькулятор для проверки функции "один к одному", показывая все шаги. Пожалуйста, введите функцию, которую вы хотите отметить, в поле ниже.
Индивидуальные функции
Этот калькулятор позволит вам оценить, является ли функция взаимно однозначной, показывая все шаги. Первое, что вам нужно сделать, это предоставить функцию. Это может быть что-то простое, линейное или квадратичное, например "y = x^2 - 1", или вы можете решить пойти на рациональная функция например 'f(x) = (x-1)/(x+3)'.
Затем, если вы удовлетворены тем, что вы предоставили, и убедились, что функция действительна, вы нажимаете кнопку "Рассчитать", чтобы получить все этапы процесса, показанные вам.
Понятие взаимно однозначной функции очень важно в алгебре и исчислении. Существует множество простых способов проверки взаимно однозначности, один из них — Тест горизонтальной линии , но из-за его природы его легче использовать, чтобы опровергнуть взаимно однозначность функции. Чтобы доказать взаимно однозначность функции, нам понадобится решение уравнений , аналитический процесс.

Что такое индивидуальный процесс
Проще говоря, однозначно-однозначная или инъективная функция — это такая функция, у которой для двух разных \(x_1\) и \(x_2\) значения их изображений через \(f(x)\) различны, что означает математически
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]Некоторые преподаватели любят писать ее немного по-другому, но все равно эквивалентно: Функция взаимно однозначна, если
\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]Это довольно изощренно говорит о том, что если график функции пересекает одно и то же значение (горизонтальную линию), то это происходит только тогда, когда точка одна и та же. Итак, все вы говорите о том, что не существует двух разных точек, в которых ее пересекает горизонтальная линия. Итак, вы просто повторяете Тест горизонтальной линии .
Как проверить, является ли функция взаимно однозначной
- Шаг 1: Начните с исходной функции f(x) и задайте уравнение y = f(x)
- Шаг 2: Попытайтесь найти х
- Шаг 3: Если вы нашли более одного решения, то функция НЕ взаимно однозначна, а если она имеет одно решение или не имеет решения, то функция взаимно однозначна
Обычно вы выполняете базовую проверку, чтобы убедиться, что эта функция явно не является однозначной, возможно, потому, что вы можете легко найти горизонтальную линию, которая приведет к сбою HLT.
Затем вы обратите внимание на некоторые основные визуальные свойства: всегда ли функция возрастает (тогда она взаимно однозначна), и то же самое относится к случаю, когда функция всегда убывает.
Как взаимно однозначно связано с нахождением обратного
Проще говоря, чтобы найти обратную функцию, функция ДОЛЖНА быть взаимно однозначной, по крайней мере, в определенном поддомене. Часто мы ограничиваем область определения, поэтому создаем функцию 1-к-1 в ограниченной области, чтобы в противном случае она не была бы 1-к-1.
Например, \(f(x) = x^2\) в целом не является однозначностью. Почему, потому что вы можете взять две разные точки \(x_1 = -1\) и \(x_2 = 1\) и обнаружить, что \(f(x_1) = (-1)^2 = 1\) и \(f(1) = 1^2 = 1\), что означает, что свойство (характеристика "один к одному")
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]не удовлетворен. Теперь, если вместо рассмотрения полной вещественной строки \(\R\) мы рассмотрим только положительные значения, мы можем заключить, что функция является взаимно однозначной для положительных действительных значений (Подсказка: в этой подобласти функция возрастает)

Существует ли формула, позволяющая оценить, является ли функция взаимно однозначной?
К сожалению нет. Я имею в виду, что \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \) можно рассматривать как формулу "один к одному", но это скорее логическое условие, чем формула.
Тем не менее, существует очень широкая общая процедура, которая используется для проверки того, является ли функция взаимно однозначной или нет, и именно это вы видите выше. Не существует формулы "один к одному". Если бы нам нужно было остановиться на одном, это должно быть y = f(x).
И мы просто находим x. Ни больше ни меньше. В конечном счете, это будет зависеть от того, что такое f(x). Очень сложная, запутанная функция может создать множество трудностей, которые необходимо решить, и, возможно, для ее решения вам понадобится калькулятор функций, и даже с калькулятором функций вы можете потерпеть неудачу.
Вы наверное думаете, а почему так?? Это потому, что по сути у нас нет методов решения ВСЕХ уравнений. Мы просто делаем то, что можем, с каким-то конкретным типом уравнений, но мы далеки от знания ТОЧНОГО способа решения всех уравнений.

Пример: функция "один к одному"
Является ли следующая функция инъективной: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)
Решение:
Нам была предоставлена следующая функция:
\[f(x) = \frac{1}{4} x + \frac{5}{4}\]Затем, чтобы оценить, является ли данная функция взаимно однозначной, нам нужно найти \(x\) и определить, существует ли решение, одно решение или несколько решений. Исходное уравнение:
\[y=\frac{1}{4}x+\frac{5}{4}\]Поместив \(x\) слева и \(y\) и константу справа, мы получим
\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]Теперь, решая \(x\), разделив обе части уравнения на \(-\frac{1}{4}\), получаем следующее:
\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]и упрощая окончательно получаем следующее
\[\displaystyle x=4y-5\]Следовательно, решение \(x\) для данного линейного уравнения приводит к \(x=4y-5\), и это только одно действительное решение, поэтому данная функция является взаимно однозначной.
Заключение
На основании найденного в предыдущем разделе можно сделать вывод, что данная функция является взаимно однозначной.
Графически:
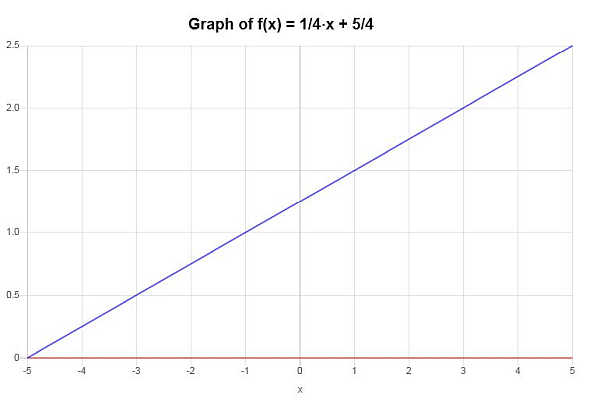
Пример: функция 1-к-1
Докажите или опровергните, что следующая функция является взаимно однозначной: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)
Решение: Чтобы оценить, является ли данная функция взаимно однозначной, нам нужно найти \(x\) и определить, существует ли решение, одно решение или несколько решений. Исходное уравнение, которое нам нужно использовать:
\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]Начальный Этап: В этом случае нам сначала необходимо упростить данное уравнение, и для этого мы проводим следующие шаги упрощения:
Итак, решения следующие:
\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]Статус "один к одному"
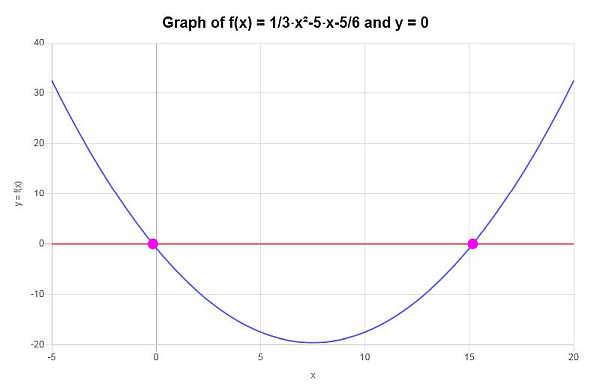
На основании работы, показанной выше, можно сделать вывод, что данная функция НЕ ЯВЛЯЕТСЯ ОДИН К ОДНОМУ, поскольку она не проходит тест горизонтальной линии, так как, например, линия \(y = 0\) является горизонтальной линией, пересекающей данную функцию. больше чем единожды.
Графически ситуацию можно изобразить следующим образом:
Еще интересные алгебраические калькуляторы
Концепция функций 1-к-1 обычно воспринимается как нечто само собой разумеющееся, но она очень важна, я бы сказал, критическая. Это связано с тем, что понятие взаимно однозначности тесно связано с представлением о монотонной функции (возрастающей или убывающей функции), равно как и тесно связано с понятием монотонной функции (возрастающей или убывающей функции) расчет обратной функции и его график.
Тем не менее, зачастую бывает трудно пройти сквозь лес за деревьями, поскольку наиболее важные понятия алгебры и исчисления тесно связаны друг с другом. Функциональный анализ — это одно из того, чем вы будете заниматься постоянно, поэтому полезно приобрести навыки, чтобы добиться успеха в этом.






