बहुपद असमानताओं के बारे में अधिक जानकारी

यह कैलकुलेटर बहुपद असमानताओं के समाधान में आपकी मदद कर सकता है, यह आपको समाधान की गणना की प्रक्रिया के सभी चरणों को दिखाता है, साथ ही समाधान को दर्शाने वाला एक असमानता ग्राफ भी प्रदान करता है।

आपके द्वारा प्रदान की गई असमानता कुछ सरल हो सकती है जैसे 'x^2 > 1', या यह कुछ अधिक जटिल हो सकती है जैसे 'x^3 + 3x^2 + 3x + 1 > 0'।

एक बार वैध बहुपद असमानता प्रदान किए जाने के बाद, कृपया आगे बढ़ें और समाधान और दिखाए गए सभी चरणों को प्राप्त करने के लिए "गणना करें" बटन पर क्लिक करें।

कृपया ध्यान रखें कि आपके द्वारा प्रदान किए गए सभी बहुपद स्वयं सटीक समाधान देने में सक्षम नहीं होंगे। बहुपद की डिग्री जितनी कम होगी, असमानता का सटीक समाधान मिलने की संभावना उतनी ही अधिक होगी।

बहुपद असमानता क्या है

बहुपद असमानता एक प्रकार की असमानता है जिसमें शामिल अभिव्यक्तियाँ बहुपद हैं, और इसका कोई भी पद गैर-बहुपद अभिव्यक्ति नहीं है। उदाहरण के लिए

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

जबकि, एक बहुपद असमानता है

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

\(\sin x\) पद की उपस्थिति के कारण, जो एक बहुपद नहीं है, एक नहीं है। असमानताओं का समाधान सामान्य तौर पर यह एक कठिन प्रक्रिया है, लेकिन बहुपद वाले लोगों के लिए, हमारे पास एक स्पष्ट कार्य योजना है।

आप बहुपद असमानता को कैसे हल करते हैं?

• Letsunt 1: सुनिश्चित करें कि सभी पद बहुपद हैं। यदि नहीं, तो बहुपदों के लिए उपयोग की जाने वाली विशिष्ट विधियाँ लागू नहीं हो सकती हैं
• Their दो दो: सब कुछ एक तरफ रख दें, दूसरी तरफ शून्य छोड़ दें
• Theirण 3: असमानता चिह्न को "=" से प्रतिस्थापित करके संबंधित समीकरण को हल करें (इसमें बहुपद का शून्य ज्ञात करना शामिल है)
• च ४: ४: असमानता के सभी महत्वपूर्ण बिंदुओं को एकत्रित करें, जो इस मामले में सहायक के वास्तविक शून्य हैं बहुपद rayrण (आप इस मामले में जटिल जड़ों पर विचार नहीं करते हैं)
• च ५: ५: यदि कोई महत्वपूर्ण बिंदु मौजूद नहीं है, तो इसका मतलब है कि अभिव्यक्ति संकेत नहीं बदलती है, इसलिए पूरी वास्तविक रेखा एक समाधान होगी, या नहीं, कोई समाधान नहीं है। जाँच करने के लिए, कोई भी बिंदु चुनें और देखें कि क्या यह असमानता को संतुष्ट करता है, और यदि यह करता है, तो पूरी वास्तविक रेखा समाधान है, यदि नहीं, तो कोई समाधान नहीं है
• च viry: 6: यदि महत्वपूर्ण बिंदु हैं, तो लगातार महत्वपूर्ण बिंदुओं के साथ अंतराल बनाएं (अपने शुरुआती महत्वपूर्ण बिंदु के रूप में -∞ का उपयोग करें, और अपने अंतिम महत्वपूर्ण बिंदु के रूप में ∞ का उपयोग करें)
• Their च 7: उनमें से प्रत्येक अंतराल की जाँच करें, और देखें कि क्या अंदर का एक बिंदु असमानता को पूरा करता है। यदि ऐसा होता है, तो अंतराल समाधान का हिस्सा है, यदि नहीं, तो अंतराल समाधान का हिस्सा नहीं है।

यहां मुख्य विचार यह है कि महत्वपूर्ण बिंदु और उनसे प्राप्त अंतराल वे अंतराल हैं जिनके लिए अभिव्यक्ति संकेत नहीं बदलती है, इसलिए या तो पूरा अंतराल एक समाधान है, या अंतराल में कोई बिंदु समाधान का हिस्सा नहीं है।

बहुपद शून्य और क्रांतिक बिंदु

बहुपद असमानताओं को हल करना संभव होने का एक कारण यह है कि महत्वपूर्ण बिंदुओं के लिए बहुपद अभिव्यक्तियों का विश्लेषण करना अपेक्षाकृत सरल है, इस तथ्य से अलग कि बहुपद निरंतर अभिव्यक्तियाँ हैं।

जैसी असमानताएं होंगी

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

जिसमें महत्वपूर्ण बिंदुओं को ढूंढना बहुत कठिन होगा। रैखिक असमानताएँ महत्वपूर्ण बिंदुओं को ढूंढना और भी आसान है, लेकिन बस इतना ही। कोई भी सामान्य असमानता अपनी जटिलताएँ प्रस्तुत करेगी।

वास्तविक जीवन में बहुपदों के अनुप्रयोग

बहुपदों के बहुत सारे अनुप्रयोग हैं। उदाहरण के लिए, भौतिकी में जब आप किनेमेटिक्स का अध्ययन करते हैं, तो न्यूटन के नियमों से प्राप्त कुछ दिलचस्प बहुपद अभिव्यक्तियाँ होती हैं। यह अभिव्यक्ति किसी पिंड की स्थिति के लिए स्थितियों को परिभाषित कर सकती है, जिससे यह निर्धारित करने के लिए बहुपद असमानता हो सकती है कि पिंड किस समय निश्चित ऊंचाई से ऊपर है, जो उदाहरण के लिए, बैलिस्टिक में महत्वपूर्ण साबित हो सकता है।

इसके अलावा, विभेदक समीकरणों का अध्ययन करते समय, आप समीकरण में डंपरिंग शब्द पा सकते हैं जो एक शक्ति पर निर्भर करते हैं, और बहुपद संरचना रखते हैं, जिसके लिए आप कुछ उन्नत असमानताओं का उपयोग कर सकते हैं, जैसे ग्रोनवॉल की असमानताएं।

उदाहरण: बहुपद असमानताओं को हल करना

हल करें: \(x^2 - x > \frac{1}{2}\)

तमाम: हमें सबसे पहले निम्नलिखित दिए गए द्विघात समीकरण \(\displaystyle x^2-x-\frac{1}{2}=0\) को हल करना होगा:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

महत्वपूर्ण बिंदुओं का विश्लेषण

आरोही क्रम में व्यवस्थित पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\)।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) के लिए: बाईं ओर सकारात्मक है, तो फिर \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) के लिए: बाईं ओर नकारात्मक है, जिसका अर्थ है कि \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) समाधान का हिस्सा है।

असमानता का समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) या \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]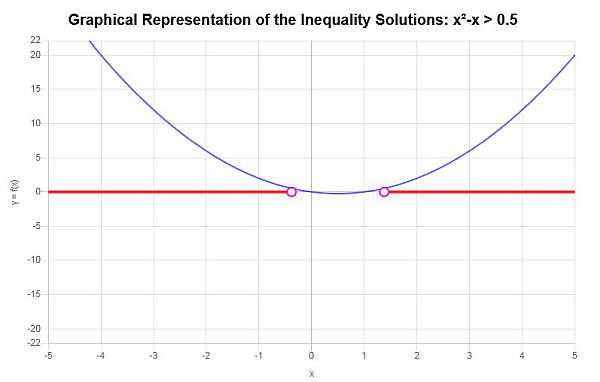

जो गणना का समापन करता है।

उदाहरण: उच्च डिग्री बहुपद

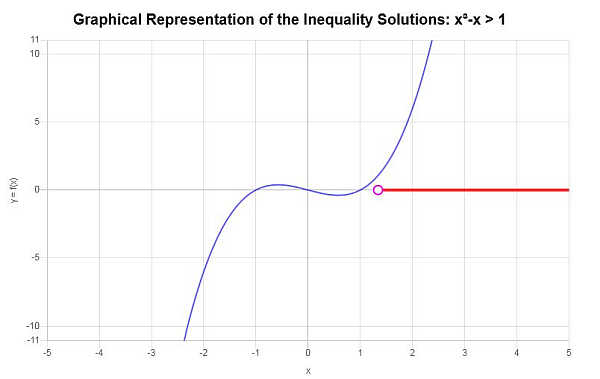
निम्नलिखित असमानता को हल करें: \(x^3 - x > 1\)

समाधान:

\(x^3-x > 1\) को हल करने के लिए हम सबसे पहले सब कुछ एक तरफ रख देते हैं:

\[x^3-x-1> 0\]

अब, इससे हमें संबंधित समीकरण प्राप्त होता है जिसे पहले हल करने की आवश्यकता है, जो \(x^3-x-1=0\) है। ध्यान दें कि डिग्री \(\displaystyle deg(p) = 3\) है, इसका अग्रणी गुणांक \(\displaystyle a_{3} = 1\) है और इसका स्थिर गुणांक \(\displaystyle a_0 = -1\) है।

तर्कसंगत जड़ों का प्रयास

हम पहले परिमेय शून्य प्रमेय के साथ सरल परिमेय मूल खोजने का प्रयास करेंगे।

अगला कार्य उन पूर्णांक संख्याओं को खोजना है जो अग्रणी गुणांक \(a_{3}\) और स्थिर गुणांक \(a_0\) को विभाजित करते हैं, जिसका उपयोग हमारे उम्मीदवारों को बहुपद समीकरण के शून्य बनाने के लिए किया जाएगा।

▹ \(a_{3} = 1\) के विभाजक हैं: \(\pm 1\).

▹ \(a_0 = -1\) के विभाजक हैं: \(\pm 1\).

इसलिए, स्थिर गुणांक \(a_0 = -1\) के प्रत्येक विभाजक को अग्रणी गुणांक \(a_{3} = 1\) के प्रत्येक विभाजक से विभाजित करने पर, हम उम्मीदवारों की निम्नलिखित सूची को मूल पाते हैं:

\[\pm \frac{ 1}{ 1}\]

अब, सभी उम्मीदवारों को यह देखने के लिए परीक्षण करने की आवश्यकता है कि क्या वे एक समाधान हैं।प्रत्येक उम्मीदवार के परीक्षण से निम्नलिखित प्राप्त किया जाता है:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

लेकिन चूंकि हमें निरीक्षण द्वारा कोई तर्कसंगत जड़ें नहीं मिली हैं, इसलिए हम प्राथमिक तरीकों का उपयोग करके कारक के साथ आगे नहीं बढ़ सकते हैं, इसलिए प्रक्रिया यहां रुक जाती है।

वैकल्पिक : यह डिग्री \(3\) का एक बहुपद है, जिसके लिए कुल \(3\) जड़ें हैं, भले ही कुछ जटिल हो सकते हैं, लेकिन इस मामले में प्राथमिक तरीकों का उपयोग करके \(3\) से कम समाधान पाए गए हैं।

उन्नत घन समीकरण विधियों का उपयोग करके, यह पाया जा सकता है कि समाधानों का पूरा सेट है:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

महत्वपूर्ण बिंदुओं का विश्लेषण

एकमात्र महत्वपूर्ण बिंदु जो पाया गया वह \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\) है।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) समाधान का हिस्सा है।

असमानता का समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x > 1.3247180451128\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left(1.3247180451128,\infty\right)\]

रेखांकन:

अधिक असमानता कैलकुलेटर

असमानताओं का समाधान (इससे वर्जित समीकरणों का समाधान खोजना ) पूरे बोर्ड में गणित में सबसे आम ऑपरेशनों में से एक है।

असमानताओं को हल करने की प्रक्रिया आमतौर पर श्रमसाध्य होती है, और सामान्य तौर पर उन्हें हल करने का कोई नियम नहीं है। बहुपद असमानताओं को हल करना कुछ अपवादों में से एक है, जिसमें हम समाधान खोजने के लिए चरणों के एक सेट का पालन कर सकते हैं, लेकिन फिर भी, हम अभी भी असफल हो सकते हैं, क्योंकि उच्च डिग्री बहुपदों से निपटना कठिन है। वास्तव में, ऐसा करना वास्तव में असंभव है बहुपद मूल खोजें एक सामान्य नियम (एबेल प्रमेय) का उपयोग करके डिग्री 5 से ऊपर।