संकेतों के डेसकार्टेस नियम का उपयोग करना

यह कैलकुलेटर आपको किसी भी दिए गए बहुपद के लिए डेसकार्टेस नियम के आवेदन के आवेदन के साथ मदद करेगा जो आप प्रदान करते हैं।इसके लिए एकमात्र आवश्यकता यह है कि बहुपद को मान्य करने की आवश्यकता है।

उदाहरण के लिए, आप x^3 - 2x + 1 जैसे सरल क्यूबिक बहुपद प्रदान कर सकते हैं, लेकिन आप एक और अधिक जटिल भी प्रदान कर सकते हैं, जैसे कि x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1, आदि।

एक बार जब आप एक वैध प्रदान करते हैं बहुपदीय फलन , आप "गणना" बटन पर क्लिक करते हैं, ताकि प्रक्रिया के सभी चरणों को प्राप्त किया जा सके।

अयस्क बीजगणित में सबसे महत्वपूर्ण कार्यों में से एक है, लेकिन यह सामान्य रूप से एक आसान काम नहीं है।सभी डिग्री के सभी बहुपदों के लिए कोई सामान्य सूत्र नहीं हैं, इसलिए हमें आमतौर पर जितनी जड़ों को खोजने के लिए एक व्यवस्थित प्रक्रिया का पालन करना पड़ता है।

इस संदर्भ में, उपलब्ध जड़ों के प्रकार के बारे में अधिक से अधिक जानकारी हमेशा उपयोगी होती है, और यह एक है जो डेसकार्टेस के संकेतों के नियमों का उद्देश्य है।

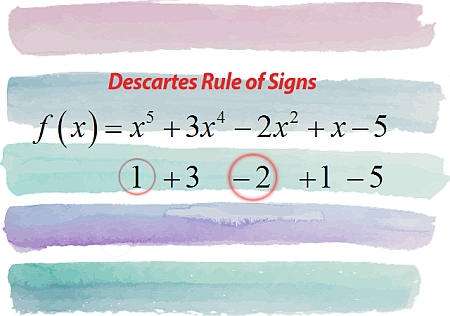
डेसकार्टेस ने संकेतों का क्या नियम कहा है?

सरल शब्दों में, डेसकार्टेस नियम का नियम आपको एक बहुपद की सकारात्मक और नकारात्मक जड़ों की संख्या के बारे में कुछ बताता है, बस दिए गए बहुपद के गुणांक के संकेतों को देखकर।

अधिक सटीक रूप से, आप प्रमुख गुणांक के साथ शुरू करते हैं, और आप शून्य गुणांक को अनदेखा करते हैं, और संकेत में परिवर्तन की गिनती करते हैं।लगातार गुणांक के संकेत में परिवर्तन की कुल संख्या \(p(x)\) की सकारात्मक जड़ों की संख्या के लिए एक ऊपरी सीमा है, और तमाम संकेतों में कुल परिवर्तनों की संख्या के समान समानता है।

फिर, आप एक ही व्यायाम करते हैं, लेकिन \(p(-x)\) के गुणांक के लिए, और आपको उस मामले में जो मिलता है, वह यह है कि लगातार गुणांक के संकेत में कुल परिवर्तन की संख्या नकारात्मक जड़ों की संख्या के लिए एक ऊपरी सीमा है \(p(x)\), और तमाम संकेत में कुल परिवर्तनों की संख्या के समान समानता है।

डेसकार्टेस नियम के नियमों को लागू करने के लिए कदम

• Letsunt 1: बहुपद P (x) का विश्लेषण करने की आवश्यकता है।सुनिश्चित करें कि यह एक बहुपद है (अन्यथा विधि काम नहीं करती है) और इसे जितना संभव हो उतना सरल करें
• Therur the: एक पंक्ति में P (x) के गुणांक डालें, अग्रणी गुणांक से शुरू, अवरोही क्रम में और शून्य गुणांक को छोड़ दें
• Theirण 3: प्रमुख गुणांक से शुरू, लगातार गुणांक के बीच साइन परिवर्तनों की गणना करें, और साइन परिवर्तनों की कुल संख्या पर ध्यान दें, और इसे कॉल करें
• Reyrur 4: P (X) के सकारात्मक शून्य की संख्या अधिकांश t पर है और इसमें T (यदि T सम है, तो भी समानता है, तो P (x) के सकारात्मक शून्य की संख्या एक समान संख्या है, और यदि T विषम है,फिर P (x) के सकारात्मक शून्य की संख्या एक विषम संख्या है)
• Reyrur 4: P (-x) के गुणांक के लिए अब एक ही प्रक्रिया को दोहराएं, P (x) के नकारात्मक शून्य की संख्या के बारे में जानकारी प्राप्त करने के लिए

यह विधि आपको संभावित रूप से सकारात्मक (और नकारात्मक) शून्य की संख्या के लिए संभावित मूल्यों की एक श्रृंखला दे सकती है, लेकिन यह संभावित रूप से आपको यह भी बता सकता है कि किसी दिए गए बहुपद के पास कितने सकारात्मक (या नकारात्मक) शून्य हैं, केवल इस बात पर निर्भर करता है कि कितने साइन परिवर्तन हैंआप गिनें।

क्या मैं इस विधि के साथ वास्तविक शून्य की गणना कर सकता हूं?

नहीं, डेसकार्टेस के संकेतों का नियम आपको इस बारे में जानकारी देने का इरादा नहीं है कि वास्तविक जड़ें क्या हैं, यह केवल आपको सकारात्मक (और नकारात्मक) जड़ों की संख्या के बारे में कुछ बताता है।

अब, इस जानकारी को मिलाकर, के साथ सरायस और अन्य प्राथमिक उपकरण, जिनमें शामिल हैं अफ़रप और यह तमाम , आप जड़ों के वास्तविक मूल्य को देखने के लिए बेहतर तरीके से सुसज्जित होंगे।

युक्तियाँ और चालें

हमेशा एक प्रकार का बहुपद पहले।उदाहरण के लिए, यदि आपके पास \(p(x) = x^5 - x^3\) है, तो आप पहले \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\) पर जाना चाहेंगे, इसलिए आप जानते हैं कि 0 एक जड़ है (गुणक 3 के साथ), और आप Dercartes नियम को \(x^2 - 1\) पर लागू करते हैंबजाय।

उदाहरण: डेसकार्टेस संकेतों का नियम

\(x^4 - x^3 + x^2 + 1\) की सकारात्मक और नकारात्मक जड़ों की संभावित संख्या को इंगित करें

तमाम: हमें निम्नलिखित बहुपद कार्य के साथ प्रदान किया जाता है: \(\displaystyle x^4 - x^3 + x^2 + 1\), जिसके लिए हमें संकेतों के डेसकार्टेस नियम को लागू करने की आवश्यकता है।

तमाम : बहुपद गुणांक (उच्चतर शक्ति के लिए उच्च के लिए) हैं:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

हम पाते हैं कि लगातार गुणांक में साइन परिवर्तन की संख्या है: \(2\), और परिवर्तन हैं: \(\,\,+1\,\,\) और << XYZC>, << xyzc> और \(\,\,+1\,\,\)।

तमाम : \(p(-x) = x^4+x^3+x^2+1\) के लिए बहुपद गुणांक हैं:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

\(p(-x)\) के गुणांक के लिए कोई संकेत परिवर्तन नहीं पाए जाते हैं।

Lenturachut: पाए गए साइन परिवर्तनों की संख्या के आधार पर, जो \(2\) है, हम निष्कर्ष निकालते हैं कि \(p(x)\) \(p(x) = x^4-x^3+x^2+1\) के लिए 0 या 2 सकारात्मक जड़ें हो सकती हैं।

अब, चूंकि \(p(-x)\) के गुणांक के लिए कोई संकेत परिवर्तन नहीं पाया गया था, इसलिए हम निष्कर्ष निकालते हैं कि \(p(x) = x^4-x^3+x^2+1\) के लिए कोई नकारात्मक शून्य नहीं हैं।

उदाहरण: अधिक डेसकार्टेस साइन रूल

\(x^4 + x^3 + x^2 - 1\) की सकारात्मक और नकारात्मक जड़ों की संभावित संख्या को इंगित करें

तमाम: अब हमें \(\displaystyle x^4 + x^3 + x^2 - 1\) का विश्लेषण करने की आवश्यकता है, डेसकार्टेस के संकेतों के साथ।

प्रदान की गई अभिव्यक्ति पहले से ही सरल है, इसलिए सरल बनाने के लिए आगे कुछ भी नहीं है।

तमाम : गुणांक हैं:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

निरीक्षण करें कि इस मामले में लगातार गुणांक में साइन परिवर्तन की संख्या \(1\) के बराबर है, और परिवर्तन हैं: \(\,\,+1\,\,\) और \(\,\,-1\,\,\)।

तमाम : \(p(-x) = x^4-x^3+x^2-1\) से जुड़े बहुपद गुणांक हैं:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

फिर, लगातार गुणांक में साइन परिवर्तन की संख्या \(3\) के समान है, और परिवर्तन हैं: \(\,\,+1\,\,\) और \(\,\,-1\,\,\), << XYZC> और \(\,\,+1\,\,\), << << \(\,\,+1\,\,\) और \(\,\,-1\,\,\)

Lenturachut: चूंकि \(p(x)\) के गुणांक के बीच एक संकेत परिवर्तन है, हम यह निष्कर्ष निकालते हैं कि \(p(x) = x^4+x^3+x^2-1\) के लिए बिल्कुल एक सकारात्मक शून्य है।

पाए गए साइन परिवर्तनों की संख्या के आधार पर, जो \(3\) है, हम निष्कर्ष निकालते हैं कि \(p(x) = x^4+x^3+x^2-1\) में 1 या 3 नकारात्मक जड़ें हो सकती हैं।

उदाहरण: सकारात्मक और नकारात्मक संकेत

\(x^4 + 1\) की सकारात्मक और नकारात्मक जड़ों की संभावित संख्या को इंगित करें।क्या आप सकारात्मक और नकारात्मक जड़ों की सटीक संख्या कुछ कह सकते हैं?

तमाम: इस मामले में कोई संकेत परिवर्तन नहीं हैं इसलिए कोई सकारात्मक जड़ें नहीं हैं।अब, \(p(-x) = (-x)^4 + 1 = x^4 + 1\), जिसमें साइन परिवर्तन नहीं है, इसलिए तब कोई नकारात्मक जड़ें नहीं हैं।निष्कर्ष यह है कि बहुपद की वास्तविक जड़ें नहीं होती हैं (चूंकि 0 एक जड़ नहीं है)।

अधिक बहुपद कैलकुलेटर

अफ़रोट कैलकुलस और बीजगणित में अधिकांश आवेदन समस्याओं के लिए एक केंद्रीय बिंदु है, और यह एक कौशल है।

एक बहुपद के शून्य की गणना में कई कौशल शामिल हैं, और तंग आपको बहुत सारी जानकारी देता है जो वास्तव में बहुपद के गुणांक को देखकर वास्तव में अनुमान लगाया जा सकता है।