समाधानकर्ताओं गणना

उलटा ट्रिग डेरिवेटिव

सराय: सभी चरणों को दिखाते हुए, व्युत्क्रम ट्रिग फ़ंक्शंस के डेरिवेटिव को खोजने के लिए इस कैलकुलेटर का उपयोग करें।कृपया उस फ़ंक्शन को टाइप करें जिसमें नीचे दिए गए फॉर्म बॉक्स में एक उलटा ट्रिग फ़ंक्शन शामिल है।

उलटा ट्रिग डेरिवेटिव

इस कैलकुलेटर के साथ आप प्रक्रिया के सभी चरणों को दिखाते हुए, व्युत्क्रम ट्रिग फ़ंक्शंस के डेरिवेटिव की गणना करने में सक्षम होंगे।

विचार यह है कि आपके द्वारा प्रदान किए जाने वाले फ़ंक्शन में एक व्युत्क्रम ट्रिग फ़ंक्शन होता है, उदाहरण के लिए f (x) = x^2/arctan (x+1), बस एक उदाहरण देने के लिए।

जब आप तैयार होते हैं और उस फ़ंक्शन को टाइप करने के लिए किया जाता है जिसे आपको अलग करने की आवश्यकता होती है, तो प्रक्रिया और गणना के सभी चरणों को देखने के लिए "गणना" बटन पर क्लिक करें।

के विचार Rairिवेटिव की kayna उलटा ट्रिग फ़ंक्शंस एक प्राकृतिक है, और हम अगले पैराग्राफ में देखेंगे कि वे सीधे से प्राप्त हो सकते हैं सराय क्या आप जानते हैं कि।

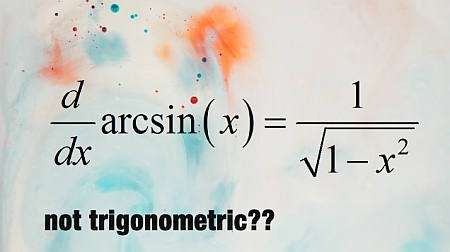
उलटा ट्रिग फ़ंक्शंस

सरल शब्दों में, उलटा ट्रिग फ़ंक्शन वे फ़ंक्शन होते हैं जो इसी ट्रिग फ़ंक्शन पर उनका मूल्यांकन करते समय होते हैं, वे पहचान की ओर ले जाते हैं।उदाहरण के लिए, यदि हम फ़ंक्शन पर विचार करते हैं \(\sin(x)\), तो इसका उलटा फ़ंक्शन \(\arcsin(x)\) है, और इस व्युत्क्रम में संपत्ति है

\[\sin(\arcsin(x)) = x \]

साथ ही

\[\arcsin(\sin(x)) = x \]

सभी के लिए \(x\) एक निश्चित अंतराल पर।तो सख्ती से, \(\arcsin(x)\) एक बीजीय बिंदु से \(\sin(x)\) का व्युत्क्रम कार्य है।और वही अन्य उलटा ट्रिग फ़ंक्शंस और उनके संबंधित ट्रिग फ़ंक्शंस के लिए जाता है।

उलटा ट्रिग डेरिवेटिव गणना

तो, अगर \(f\) एक फ़ंक्शन है, और इसका एक व्युत्क्रम है \(f^{-1}\), तो हमारे पास वह है

\[f^{-1}(f(x)) = x\]

सभी के लिए \(x\)।फिर, यदि हम समानता के दोनों किनारों को अलग करते हैं, और हम बाईं ओर श्रृंखला नियम का उपयोग करते हैं, तो हमें मिलता है

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

अब, अगर हम \(y = f(x)\) सेट करते हैं, तो \(x = f^{-1}(y)\)

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

हम इसका उपयोग उलटा ट्रिग फ़ंक्शंस के लिए कैसे करते हैं?मान लें \(f(x) = \sin(x)\) और \(f^{-1}(x) = \arcsin(x)\)।फिर, एक फ़ंक्शन के व्युत्पन्न और इसके व्युत्क्रम के व्युत्पन्न के बीच सामान्य संबंध के अनुसार, हमें मिलता है

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

लेकिन एक साफ ज्यामितीय चाल हमें बताती है कि

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

जिसका अर्थ है कि

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

व्युत्क्रम ट्रिग डेरिवेटिव के बाकी समान तर्क के साथ प्राप्त किए जाते हैं।

6 बुनियादी उलटा ट्रिग फ़ंक्शंस क्या हैं?

#1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
#2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
#3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
#4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
#5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
#6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

दिलचस्प रूप से पर्याप्त है, जब उलटा ट्रिग कार्यों के व्युत्पन्न की गणना करते हैं, तो उलटा ट्रिग डेरिवेटिव में से कोई भी ट्रिग फ़ंक्शन या उलटा ट्रिग फ़ंक्शन शामिल नहीं होता है।

व्युत्क्रम त्रिकोणमितीय कार्यों के व्युत्पन्न के अनुप्रयोग

ट्रिग फ़ंक्शंस और उनके डेरिवेटिव, साथ ही उलटा ट्रिग फ़ंक्शंस और उनके डेरिवेटिव अधिक जटिल कार्यों को बनाने के लिए बिल्डिंग ब्लॉक के रूप में उपयोग किए जाने वाले बुनियादी कार्यों और संचालन की सूची का हिस्सा बनाते हैं।

यद्यपि ट्रिग फ़ंक्शन उलटा ट्रिग फ़ंक्शंस की तुलना में अनुप्रयोगों में अधिक बार दिखाई देंगे, बाद वाले में कैलकुलस में एक स्पष्ट स्थान भी होता है, खासकर जब आंशिक अंश अपघटन विधि का उपयोग करना और उपयोग करना।

युक्तियाँ और चालें

यह मत भूलो कि व्युत्क्रम ट्रिग फ़ंक्शंस के डेरिवेटिव बेहद उपयोगी हो सकते हैं, खासकर जब उन शब्दों को एकीकृत करते हैं जिनमें एक द्विघात भाजक होता है।

इसके अलावा, गलतियाँ करना आसान है जब परिभाषा के अनुसार उलटा ट्रिग डेरिवेटिव की गणना करते हैं, तो आप निश्चित रूप से उपयोग करने से लाभान्वित हो सकते हैं वthaumaumaut r कैलकुलेटry यह चरणों को दिखाएगा, या जिसका उपयोग आप अपने काम की जांच करने के लिए कर सकते हैं।

उदाहरण: उलटा ट्रिग डेरिवेटिव

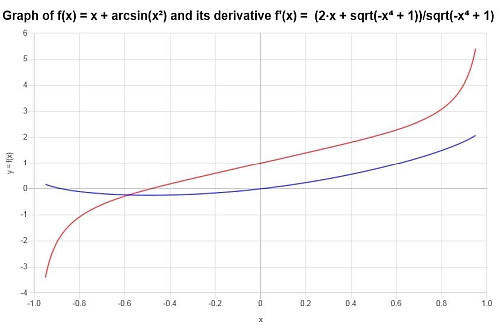
की गणना: \(f(x) = x + \arcsin(x^2)\)

तमाम: इस पहले उदाहरण के लिए, हम \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\) का विश्लेषण करेंगे।इस फ़ंक्शन में एक व्युत्क्रम ट्रिग फ़ंक्शन शामिल है, जो किसी अन्य फ़ंक्शन के साथ मिश्रित होता है।चलो इसके व्युत्पन्न की गणना करते हैं:

\( \displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

But we know already that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

By using the Chain Rule: \(\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}\)

कड़ा : हम यह निष्कर्ष निकाल सकते हैं कि फ़ंक्शन का व्युत्पन्न है:

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

हम निम्नलिखित ग्राफ में फ़ंक्शन और इसके व्युत्पन्न दोनों को देख सकते हैं:

उदाहरण: अधिक उलटा ट्रिग डेरिवेटिव

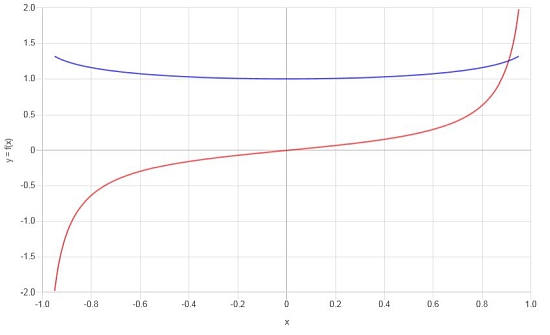
निम्नलिखित फ़ंक्शन पर विचार करें: \(f(x) = \frac{\arcsin(x)}{x}\), इसके व्युत्पन्न की गणना करें।

तमाम: अब दूसरे उदाहरण के लिए, हमारे पास फ़ंक्शन है \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\)।

\( \displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)\)

The Quotient Rule applies in this case: \(\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\)

तमाम : हम जिस व्युत्पन्न की तलाश कर रहे हैं, वह है:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

ग्राफिक रूप से, हमारे पास निम्नलिखित है:

उलटा ट्रिग डेरिवेटिव उदाहरण

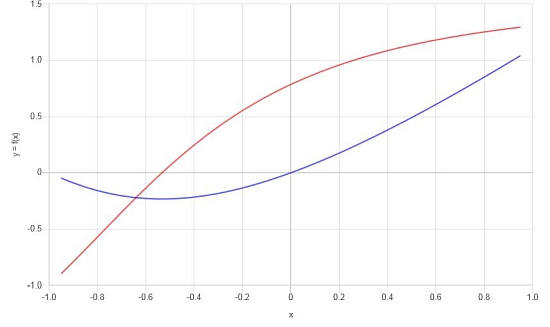
की गणना: \(f(x) = x \arctan(x+1)\)

तमाम: अब इस अंतिम उदाहरण के लिए, हम फ़ंक्शन \(\displaystyle f(x)=x\arctan\left(x+1\right)\) के साथ काम करेंगे, जिसमें एक उलटा फ़ंक्शन होता है।

\( \displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)\)

The Product Rule applies in this case: \(\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)\)

We expand the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Reducing the one in \(x\cdot 1 = x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\)

तिहाई : सरलीकरण के बाद, व्युत्पन्न है:

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

पाए गए परिणामों के आधार पर, हम F और F के लिए निम्नलिखित ग्राफ का निर्माण कर सकते हैं:

अन्य कैलकुलस कैलकुलेटर

उपयोग करते समय सराय , हमने कहा कि वे बुनियादी लागू करने के लिए महत्वपूर्ण भवन ब्लॉक थे वmuntumam नियम ।

व्युत्क्रम ट्रिग फ़ंक्शंस के लिए डेरिवेटिव को बस से प्राप्त किया जा सकता है तमाम बुनियादी ट्रिग डेरिवेटिव, और यही कारण है कि हम उन्हें सीखने या यहां तक कि याद करने के लिए बुनियादी डेरिवेटिव के समूह के भीतर भी मानते हैं।