كيف تعمل حاسبة الانحدار اللوغاريتمي

ستتيح لك هذه الآلة الحاسبة تقدير الانحدار اللوغاريتمي لبيانات العينة التي تقدمها في جدول بيانات إدخال البيانات المقابل.

عندما يتم توفير بيانات صالحة (في هذه الحالة, يمكن للمتغير X أن يأخذ قيمًا موجبة فقط), بعد النقر فوق "حساب", ستحصل على سلسلة من الخطوات المشاركة في العملية بالإضافة إلى رسم بياني تشتت يوضح جودة الملاءمة.

لاحظ أنه عندما تكون البيانات صالحة من حيث الأبعاد, يمكنك دائمًا تشغيل الانحدار اللوغاريتمي, ولكن هذا لا يعني أن النتائج ستكون ذات جودة جيدة, على الأقل من حيث الملاءمة.

أدوات وحاسبات للانحدار اللوغاريتمي

توجد أدوات مختلفة يمكنك استخدامها لتقدير الانحدار اللوغاريتمي. من الناحية النظرية, يمكنك القيام بالأمور يدويًا, باستخدام تحويل اللوغاريتم باستخدام آلة حاسبة عادية ربما (حتى تلك التي تأتي مع هاتفك), ثم استخدام معادلة المربعات الصغرى المساعدة للعثور على نموذج اللوغاريتم, وهو

\[ Y = a + b \ln(X) + \varepsilon \]

من المؤكد أن القيام بذلك يدويًا قد يكون مرهقًا ومعرضًا للخطأ, على أقل تقدير. ولهذا السبب يعد استخدام هذا الخيار خيارًا جيدًا للغاية حاسبة الانحدار اللوغاريتمي لأنه يقوم بكل العمل نيابة عنك ويوضح لك كل الخطوات

هناك أدوات أخرى مثل تطبيقات الهاتف المحمول التي من المفترض أن تقوم بجميع أنواع الانحدار, ولكنك ستحتاج إلى المحاولة ورؤية ذلك لأن هذا قد يكون بمثابة موقف غير مؤكد.

خطوات تشغيل الانحدار اللوغاريتمي

• الخطوة 1: قم بإدراج المتغير المستقل (X) والمتغير التابع (Y) بشكل واضح, وتأكد من أن كلا المتغيرين لهما نفس حجم العينة
• الخطوة 2: تأكد من أن قيم X موجبة, وإلا فلن تتمكن من تشغيل الانحدار
• الخطوه 3: إنشاء متغير مستقل جديد X* = ln(X) عن طريق تطبيق تحويل اللوغاريتم الطبيعي
• الخطوة 4: يمكنك الآن تشغيل تحليل الانحدار الخطي المنتظم لـ X* مقابل Y

أحد الأشياء التي يجب وضعها في الاعتبار هو أنه من المستحسن تمامًا استخدام الآلة الحاسبة أو البرنامج للحصول على إحصائيات تشخيصية تساعدك في تقييم ما إذا كان من المنطقي استخدام نموذج الانحدار اللوغاريتمي .

استخدام برنامج excel مقابل استخدام حاسبات الانحدار اللوغاريتمي المخصصة

يلعب Excel دورًا مهمًا في مساعدتك على إجراء تحليل إحصائي أساسي: فهو يوفر لك واجهة نظيفة ومثبتة لتشغيل الاختبارات الأساسية, بما في ذلك حساب الانحدار اللوغاريتمي.

المشكلة الرئيسية في برنامج Excel هي أنه لا يوفر لك خطوة الحل. وقد يساعد هذا في ظهور أطر عمل الذكاء الاصطناعي مثل Copilot, والتي من المرجح أن تمنح برنامج Excel خطوات وصفية للحساب.

فهم وتفسير نتائج حاسبة الانحدار

مثل أي شيء آخر تحليل الانحدار بالنسبة للحالة اللوغاريتمية, لا تختلف في أنك ستلقي نظرة على إحصائيات ملاءمة النموذج, مثل إحصاءات F لاختبار أهمية النموذج بشكل عام, و إحصاءات t للأهمية الفردية للمتنبئين .

أيضًا, من المحتمل أن ترغب في إلقاء نظرة على التباين والخطأ الموضحين, و معاملات R^2 وR^2 المعدلة , والتي ستوفر لك تقديرات للتغير الموضح للمتغير التابع حسب النموذج.

أمثلة الانحدار اللوغاريتمي

ضع في اعتبارك المتغيرات

س: 1, 2, 3, 4, 5

و: 15, 25, 28, 29, 30

تقدير نموذج الانحدار اللوغاريتمي.

حل:

يتم توفير البيانات التالية لمتغيري X وY لبناء نموذج الانحدار اللوغاريتمي:

إكس	و
1	15
2	25
3	28
4	29
5	30

المتغير المستقل الذي سنستخدمه هو اللوغاريتم الطبيعي لـ X, والمتغير التابع هو Y. ولحساب معاملات الانحدار لهذا الانحدار المساعد, يجب استخدام الجدول التالي:

	إكس	ز = ل ن (س)	و	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

بناءً على الجدول أعلاه, يتم حساب ما يلي:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

لذلك, بناءً على الحسابات المذكورة أعلاه, يتم الحصول على معاملات الانحدار (الميل \(m\), والتقاطع مع المحور y \(n\)) على النحو التالي:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

وبالتالي نجد أن معادلة الانحدار هي:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

ولكن بما أن المتغير المساعد \(Z = \ln(X)\), فإننا نستنتج أن معادلة الانحدار اللوغاريتمي هي:

\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

لذلك, بناءً على المعلومات المقدمة أعلاه, يتم الحصول على مخطط التشتت ومخطط الانحدار التاليين:

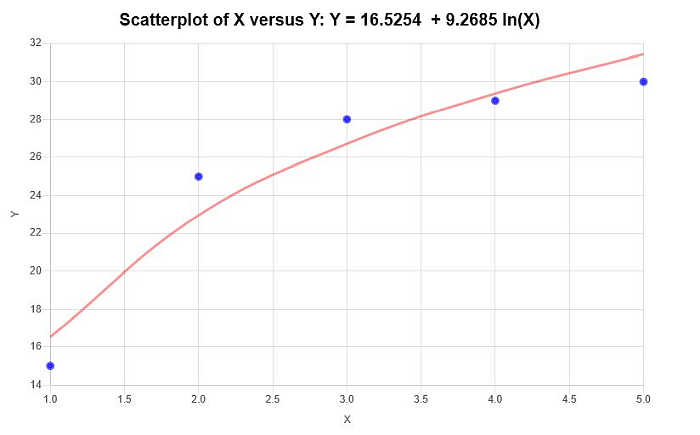
المزيد من الآلات الحاسبة الإحصائية

قد تكون أيضا مهتما ب حساب الانحدار الأسي , أو العمل على حل التفاصيل الدقيقة لـ الانحدار متعدد الحدود , والتي تنطبق جميعها في سياقات مختلفة, استنادًا إلى سلوك بيانات العينة المرصودة.

من المرجح أنك سوف ترغب في بناء مؤامرة مبعثرة من أجل تقييم السلوك التجريبي للبيانات, وللتقييم المسبق ما إذا كان الانحدار اللوغاريتمي ينطبق بدلاً من نوع مختلف من الانحدار.