求解根式方程

通过这个根式方程求解器,你可以处理所提供的根式方程,对其进行代数运算,同时向你展示运算过程的所有步骤。

这个求解器可以接受任何涉及根的有效方程,比如 "sqrt(x) = 1 "这样非常简单的方程,或者 "sqrt(x+3) = x^2 - 1 "这样比较难解的方程。

一旦提供了有效的基式方程,基本上就完成了,剩下的工作就是点击 "求解",这样就能显示过程的所有步骤。

强基方程的求解依赖于有效的 代数运算表达式 以便从根本上消除激进部分。

什么是根式方程

用极其简单的话来说,根式方程是一种 数学方程 其中未知数（通常为 x）位于一个基数内。例如

\[\displaystyle \sqrt x = x^2 \]

是一个根式方程,因为有 \( \sqrt x\),但方程

\[\displaystyle 2 x = x^2 \]

例如,这不是一个根式方程,因为我们无法在方程中的任何地方 x 根式的内 部。

如何解根式方程

只要遵循以下步骤,求解根式方程并不难：

有时,无论如何进行适当的分组和简化,都无法完全消除偏旁部首,或者会导致方程更加复杂。

化简根式方程

如上所述,成功计算涉及根的方程在很大程度上取决于能否 化简 .但有时这还不够,因为化简所有出现的部首并不能使它们消失。最常见的方法是先还原偏旁部首,然后应用平方（2 的幂次）来取消偏旁部首。

但是,用平方来消除根号是一把双刃剑,因为通过平方,任何相关符号都可能消失。因此,在 "消除 "偏旁部首并找到辅助方程的解时,我们必须仔细检查辅助解是否也是原方程的解。很多时候,它们并不是。

另一种方法是使用适当的替换来查看消除基式的过程。例如,对于基式方程

\[\displaystyle \sqrt x = x \]

你可能想设置 \(u = \sqrt x\),那么 \(u^2 = (\sqrt x)^2 = x\),这样原方程就变成了下面的辅助方程：

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

这是一个我们可以求解的多项式方程。因此,使用代入法可以将我们不知道如何求解的方程转化为 解多项式方程 我们知道该由谁来解决。

我们为什么要关注根式方程？

根式方程是代数和微积分中经常出现的,因为它们是许多不同现象建模的基础。

当 x 接近无穷大时,根式函数的性质和缓慢增长类型非常有趣。

例题求解涉及根式的方程

解决以下问题：\(\sqrt{x} = 2x\)

解决方案：

下面是一个方程。我们需要求解这个只有一个变量,即 \(x\)的方程,因此目标是求解 \(x\)：

\[\sqrt{x}=x^2\]

请注意,给定多项式的阶数为 \(\displaystyle deg(p) = 4\),前导系数为 \(\displaystyle a_{4} = -1\),常数系数为 \(\displaystyle a_0 = 0\)。

尝试合理的根源

有理根的候选者 :由于 \(p(x)\) 中第一个系数不为零的项是 \(x\),所以我们可以将这一项因式分解,得到

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

但括号内的项的度数大于2,所以没有基本公式来分解它。我们需要测试可能的有理根。

接下来的任务是找出前导系数 \(a_{3}\) 和常数系数 \(a_0\) 相除的整数,用来构建多项式方程的候选零点。

因此,用常数系数 \(a_0 = 1\) 的每个除数除以前导系数 \(a_{3} = -1\) 的每个除数,我们会发现以下候选根的列表：

\[\pm \frac{ 1}{ 1}\]

现在,需要对所有的候选人进行测试,看他们是否是一个解决方案。以下是测试每个候选人得到的结果。

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

多项式除法 :由于我们没有足够的有理候选根,我们将 \(\displaystyle -x^3+1\) 除以从有理根导出的因数的乘积,即 \(\displaystyle \left(x-1\right) \)。

步骤1： 红利 \(\displaystyle p(x) = -x^3+1\) 的前项是 \(\displaystyle -x^3\),而除数 \(\displaystyle s(x) = x-1\) 的前项等于 \(\displaystyle x\)。

因此,我们需要乘以 \(x\) 来得到红利的前项是 \(\displaystyle \frac{ -x^3}{ x} = -x^2\),所以我们把这一项加到商中。同时,我们用这一项乘以除数,得到 \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\),然后再减去这一项：

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

第2步： 现在,当前余数 \(\displaystyle -x^2+1\) 的前项是 \(\displaystyle -x^2\),我们知道除数的前项是 \(\displaystyle x\)。

因此,我们需要乘以 \(x\) 以得到当前余数的前项是 \(\displaystyle \frac{ -x^2}{ x} = -x\),所以我们要把这一项加到商中。同时,我们将其与除数相乘,得到 \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\),我们需要将其减去当前的余数：

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

第3步： 现在,当前余数 \(\displaystyle -x+1\) 的前项是 \(\displaystyle -x\),我们知道除数的前项是 \(\displaystyle x\)。

因此,我们需要乘以 \(x\) 以得到当前余数的前项是 \(\displaystyle \frac{ -x}{ x} = -1\),所以我们要把这一项加到商中。同时,我们将其与除数相乘,得到 \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\),我们需要将其减去当前的余数：

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

因此,商为 \(\displaystyle q(x) = -x^2-x-1\),余数为 \(\displaystyle r(x) = 0\)。

因此,在除法之后,我们在因式分解中推进了与

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

但现在,由于求得的商 \(\displaystyle -x^2-x-1\) 是二次方,我们可以找到它的根,看看能否在实域上对它进行因式分解。

我们需要解下面给出的一元二次方程 \(\displaystyle -x^2-x-1=0\)。

使用二次方程

对于形式为 \(a x^2 + bx + c = 0\) 的一元二次方程,根的计算公式如下：

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

在这种情况下,我们需要求解的方程是 \(\displaystyle -x^2-x-1 = 0\),这意味着相应的系数是：

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

在这种情况下,我们得到的判别式是 \(\Delta = \displaystyle -3 < 0\),是负数,因此我们知道给定方程有两个不同的共轭复根。

现在,将这些数值插入到根的公式中,我们可以得到。

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

因此,我们发现。

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

因此,在找到最后一个二次部分的根之后,我们发现了两个复根,所以我们无法在实域中对项 \(-x^2-x-1\) 进行因式分解,因此我们以 \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\) 结束这一过程。

因此,对给定的多项式方程求解 \(x\),就可以利用因式分解数学模型求得 \(x = \, \)\(0\),\(1\),\(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\),\(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\)。

检查辅助解决方案

根据辅助多项式方程对这些解进行检验后发现,并非所有候选解都是原方程的解。原始方程的唯一实际解是

\[x_1=0 \]
\[x_2=1 \]

因此,对给定方程求解 \(x\),可得到解 \(x=0,\,\,x=1\)。

图形化

下面是所得到的解决方案的图示：

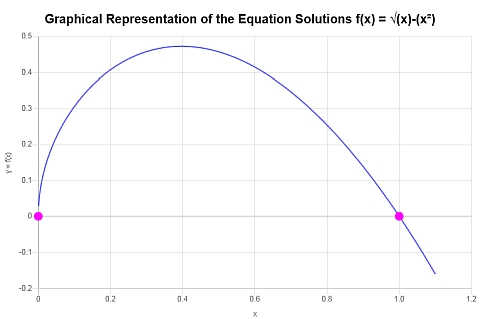
这就结束了计算。

其他有用的方程求解器

求解根式方程时,与需要 求解线性方程 或当您需要 解二次方程 ,属于需要巧妙的代数运算才能求出 x 的方程。

换句话说,你不会有 "这样做就一定能成功 "的想法。你所进行的操作类型将取决于方程的结构,而且在不同的情况下会有很大的不同。

简化表达式 首先是一个好的做法,因为你可以减少可能干扰方程整体结构的术语。