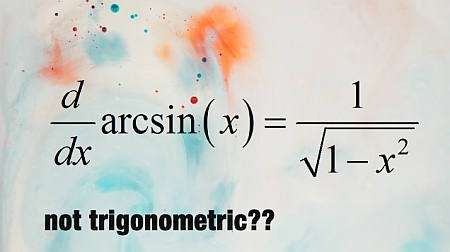反三角导数
使用此计算器,您将能够计算反三角函数的导数,显示过程的所有步骤。
这个想法是你提供的函数包含一个反三角函数,例如f(x) = x^2/arctan(x+1),只是举个例子。
当您准备好并完成输入需要区分的函数时,单击"计算"按钮以查看过程和计算的所有步骤。
的想法
计算导数
的反三角函数是自然的,我们将在下一段中看到它们可以直接从
三角导数
你知道的。
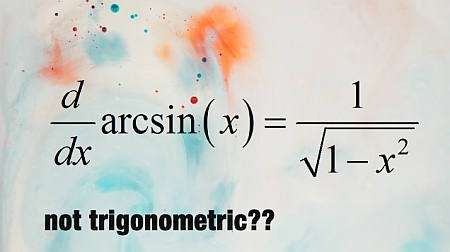
反三角函数
简单来说,反三角函数是那些在相应的三角函数上评估它们时,它们导致恒等式的函数。例如,如果我们考虑函数 \(\sin(x)\),它的反函数是 \(\arcsin(x)\),这个反函数具有以下性质
\[\sin(\arcsin(x)) = x \]
也
\[\arcsin(\sin(x)) = x \]
对于某个时间间隔内的所有 \(x\)。所以严格来说,\(\arcsin(x)\)从代数的角度来看是\(\sin(x)\)的反函数。其他反三角函数及其对应的三角函数也是如此。
反三角导数计算
那么,如果 \(f\) 是一个函数,并且它有一个反函数 \(f^{-1}\),那么我们有
\[f^{-1}(f(x)) = x\]
对于所有 \(x\)。然后,如果我们对等式的两边进行微分,并在左侧使用链式法则,我们得到
\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\]
\[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]
现在,如果我们设置 \(y = f(x)\),那么 \(x = f^{-1}(y)\),这将导致
\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\]
\[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]
我们如何将其用于反三角函数?假设 \(f(x) = \sin(x)\) 和 \(f^{-1}(x) = \arcsin(x)\)。那么,根据函数的导数与其逆函数的导数之间的一般关系,我们得到
\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\]
\[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]
但是一个巧妙的几何技巧告诉我们
\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]
这意味着
\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]
其余的反三角导数都是用类似的论证得到的。
6 个基本的反三角函数是什么?
-
#1:
\( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
-
#2:
\( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
-
#3:
\( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
-
#4:
\( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
-
#5:
\( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
-
#6:
\( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)
有趣的是,在计算反三角函数的导数时,没有一个反三角导数涉及三角函数或反三角函数。
反三角函数导数的应用
三角函数及其导数,以及反三角函数及其导数构成了基本函数和运算清单的一部分,用作构建块,用于创建更复杂的函数。
虽然三角函数在应用中会比反三角函数更频繁地出现,但后者在微积分中也有明显的地位,尤其是在微分和使用部分分数分解法时。

技巧和窍门
不要忘记,反三角函数的导数可能非常有用,尤其是在对具有二次分母的项求积分时。
此外,根据定义计算反三角导数时很容易出错,使用
衍生品计算器
它将显示步骤,或者您可以使用它来检查您的工作。

示例:反三角导数
计算以下的导数\(f(x) = x + \arcsin(x^2)\)的导数
解决方案:
对于第一个示例,我们将分析 \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\)。该函数涉及一个反三角函数,与另一个函数复合。让我们计算它的导数:
\( \displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)\)
By linearity, we know \(\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)
But we know already that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)
By using the Chain Rule: \(\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)
\( \displaystyle = \,\,\)
\(\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)
In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}\)
\( \displaystyle = \,\,\)
\(\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}\)
回答
:我们可以得出结论,函数的导数是:
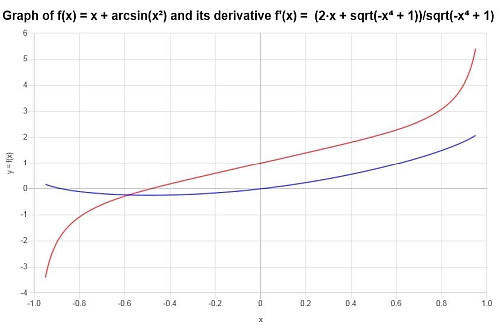
\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]
我们可以在下图中看到函数及其导数:
例子:更多的反三角导数
考虑以下函数:\(f(x) = \frac{\arcsin(x)}{x}\),计算其导数。
解决方案:
现在对于第二个例子,我们有函数\(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\)。
\( \displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)\)
The Quotient Rule applies in this case: \(\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)
We already know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}\)
Directly differentiating: \(\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}\)
Finally, the following is obtained
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\)
最后的结论
:我们要找的导数是:
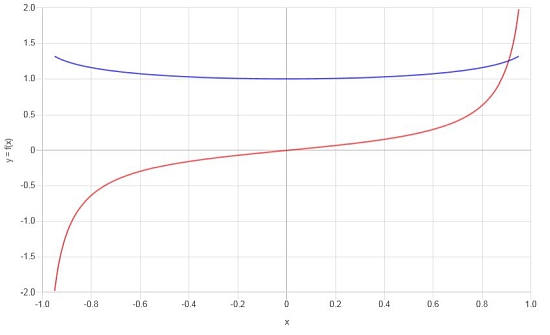
\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]
从图形上看,我们有以下内容:
反三角导数示例
计算以下的导数\(f(x) = x \arctan(x+1)\)的导数
解决方案:
现在对于最后一个示例,我们将使用函数 \(\displaystyle f(x)=x\arctan\left(x+1\right)\),它包含一个反函数。
\( \displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)\)
The Product Rule applies in this case: \(\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)
Using the Chain Rule: \(\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)
By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}\)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}\)
We know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)\)
We expand the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)
Reducing the one in \(x\cdot 1 = x\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)
Finally, the following is obtained
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\)
结论
:化简后导数为:
\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]
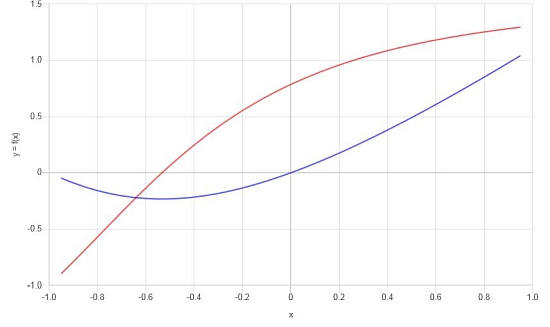
根据找到的结果,我们可以为 f 和 f' 构造如下图:
其他微积分计算器
使用时
三角导数
,我们说它们是应用基础知识的重要组成部分
衍生品规则
.
反三角函数的导数可以简单地从
衍生品
的基本三角导数,这就是为什么我们也将它们视为要学习甚至记忆的基本导数组。