Как работает калькулятор логарифмической регрессии

Этот калькулятор позволит вам оценить логарифмическую регрессию для выборочных данных, которые вы предоставляете в соответствующей таблице входных данных.

Если предоставлены допустимые данные (в этом случае переменная X может принимать только положительные значения), после нажатия кнопки "Рассчитать" вы получите последовательность шагов, включенных в процесс, а также диаграмму рассеяния, которая покажет качество подгонки.

Обратите внимание, что если данные размерно достоверны, вы всегда можете запустить логарифмическую регрессию, но это не означает, что результаты будут хорошего качества, по крайней мере с точки зрения соответствия.

Инструменты и калькуляторы для логарифмической регрессии

Существуют различные инструменты, которые вы можете использовать для оценки вашей логарифмической регрессии. Теоретически вы можете делать все вручную, используя логарифмическое преобразование с помощью обычного калькулятора, возможно (даже тех, которые идут в комплекте с вашим телефоном), а затем использовать вспомогательное уравнение наименьших квадратов, чтобы найти логарифмическую модель, которая

\[ Y = a + b \ln(X) + \varepsilon \]

Конечно, подход, который делается вручную, может быть утомительным и подверженным ошибкам, мягко говоря. Вот почему это очень хороший вариант использовать это Калькулятор логарифмической регрессии , потому что он делает всю работу за вас и показывает вам все шаги

Существуют и другие инструменты, например, приложения для мобильных телефонов, которые, как предполагается, выполняют все типы регрессии, но вам нужно будет попробовать и посмотреть, потому что это может быть как удачная, так и неудачная ситуация.

Шаги для запуска логарифмической регрессии

• Шаг 1: Четко перечислите независимую переменную (X) и зависимую переменную (Y) и убедитесь, что обе переменные имеют одинаковый размер выборки
• Шаг 2: Убедитесь, что ваши значения X положительны, в противном случае вы не сможете запустить регрессию
• Шаг 3: Построить новую независимую переменную X* = ln(X) путем применения преобразования натурального логарифма
• Шаг 4: Теперь вы запускаете обычный линейный регрессионный анализ для X* по сравнению с Y

Следует помнить, что настоятельно рекомендуется использовать калькулятор или программное обеспечение для получения диагностической статистики, которая поможет вам оценить, имеет ли смысл использовать данный метод модель логарифмической регрессии .

Использование excel и специализированных калькуляторов логарифмической регрессии

Excel играет важную роль в проведении базового статистического анализа: он предоставляет вам понятный и проверенный интерфейс для выполнения базовых тестов, включая расчет логарифмической регрессии.

Основная проблема Excel в том, что он не предоставит вам шаг решения. Это может помочь с появлением фреймворков ИИ, таких как Copilot, которые, скорее всего, наделят Excel описательными шагами расчета.

Понимание и интерпретация результатов калькулятора регрессии

Как и любой другой Регрессивный анализ , для логарифмического случая нет ничего особенного в том, что вы будете рассматривать статистику соответствия модели, такую как F-статистика для проверки значимости модели в целом и t-статистика для индивидуальной значимости предикторов .

Кроме того, вы, вероятно, захотите взглянуть на объясненные отклонения и ошибки, а также Коэффициенты R^2 и скорректированные коэффициенты R^2 , который предоставит вам оценки объясненной вариации зависимой переменной с помощью модели.

Примеры логарифмической регрессии

Рассмотрим переменные

Х: 1, 2, 3, 4, 5

И: 15, 25, 28, 29, 30

Оцените модель логарифмической регрессии.

Решение:

Для построения модели логарифмической регрессии предоставляются следующие данные для переменных X и Y:

Х	И
1	15
2	25
3	28
4	29
5	30

Независимой переменной, которую мы будем использовать, является натуральный логарифм X, а зависимой переменной — Y. Чтобы вычислить коэффициенты регрессии для этой вспомогательной регрессии, необходимо использовать следующую таблицу:

	Х	Z = ln(X)	И	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

На основании приведенной выше таблицы рассчитывается следующее:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Таким образом, на основании приведенных выше расчетов коэффициенты регрессии (наклон \(m\) и точка пересечения с осью Y \(n\)) получаются следующим образом:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Таким образом, мы получаем, что уравнение регрессии имеет вид:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Но поскольку вспомогательная переменная \(Z = \ln(X)\), то заключаем, что уравнение логарифмической регрессии имеет вид:

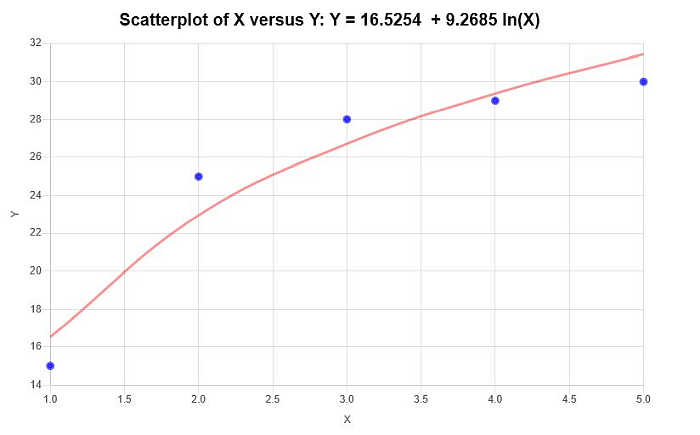
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Таким образом, на основании предоставленной выше информации получены следующие диаграмма рассеяния и диаграмма регрессии:

Больше статистических калькуляторов

Вам также может быть интересно вычисление экспоненциальной регрессии , или отработка тонкостей Полиномиальная регрессия , каждый из которых применяется в разных контекстах, в зависимости от поведения наблюдаемых выборочных данных.

Вероятно, вам захочется построить диаграмму рассеяния для оценки эмпирического поведения данных и предварительной оценки того, применима ли логарифмическая регрессия вместо другого типа регрессии.