लॉगरिदमिक रिग्रेशन कैलकुलेटर कैसे काम करता है

यह कैलकुलेटर आपको संबंधित डेटा इनपुट स्प्रेडशीट में आपके द्वारा प्रदान किए गए नमूना डेटा के लिए लघुगणकीय प्रतिगमन का अनुमान लगाने की अनुमति देगा।

जब वैध डेटा प्रदान किया जाता है (इस मामले में, एक्स चर केवल सकारात्मक मान ले सकता है), जब आप "गणना" पर क्लिक करते हैं, तो आपको प्रक्रिया में शामिल चरणों की एक सूची मिलेगी और साथ ही एक स्कैटरप्लॉट भी मिलेगा जो फिट की गुणवत्ता दिखाएगा।

ध्यान दें कि जब डेटा आयामी रूप से वैध होता है, तो आप हमेशा लॉगरिदमिक प्रतिगमन चला सकते हैं, लेकिन इसका मतलब यह नहीं है कि परिणाम अच्छी गुणवत्ता के होंगे, कम से कम फिट के संदर्भ में।

लघुगणकीय प्रतिगमन के लिए उपकरण और कैलकुलेटर

अपने लघुगणक प्रतिगमन का अनुमान लगाने के लिए आप विभिन्न उपकरणों का उपयोग कर सकते हैं। सिद्धांत रूप में, आप मैन्युअल रूप से काम करके, शायद एक नियमित कैलकुलेटर (यहां तक कि जो आपके फोन के साथ आते हैं) का उपयोग करके लॉग ट्रांसफ़ॉर्मेशन का उपयोग करके आगे बढ़ सकते हैं, और फिर लॉग मॉडल को खोजने के लिए एक सहायक कम से कम वर्ग समीकरण का उपयोग कर सकते हैं, जो कि है

\[ Y = a + b \ln(X) + \varepsilon \]

निश्चित रूप से, हाथ से ऐसा करना थकाऊ और त्रुटिपूर्ण हो सकता है, कम से कम इतना तो कहना ही होगा। इसलिए इसका उपयोग करना एक बहुत अच्छा विकल्प है लघुगणकीय प्रतिगमन कैलकुलेटर , क्योंकि यह आपके लिए सभी काम करता है और यह आपको सभी चरण दिखाता है

मोबाइल फोन एप्स जैसे अन्य उपकरण भी हैं जो सभी प्रकार के प्रतिगमन करने में सक्षम हैं, लेकिन आपको प्रयास करके देखना होगा, क्योंकि यह सफल या असफल जैसी स्थिति हो सकती है।

लघुगणकीय प्रतिगमन चलाने के चरण

• स्टेप 1: स्वतंत्र चर (X) और आश्रित चर (Y) को स्पष्ट रूप से सूचीबद्ध करें, और सुनिश्चित करें कि दोनों चरों का नमूना आकार समान हो
• चरण दो: सुनिश्चित करें कि आपके X के मान सकारात्मक हैं, अन्यथा आप प्रतिगमन नहीं चला सकते
• चरण 3: प्राकृतिक लॉग रूपांतरण लागू करके एक नया स्वतंत्र चर X* = ln(X) बनाएँ
• चरण 4: अब आप X* बनाम Y के लिए एक नियमित रैखिक प्रतिगमन विश्लेषण चलाते हैं

एक बात ध्यान में रखें कि निदान संबंधी आंकड़े प्राप्त करने के लिए कैलकुलेटर या सॉफ्टवेयर का उपयोग करना पूरी तरह से उचित है, जो आपको यह आकलन करने में मदद करेगा कि इसका उपयोग करना उचित है या नहीं। लघुगणकीय प्रतिगमन मॉडल .

एक्सेल बनाम समर्पित लघुगणक प्रतिगमन कैलकुलेटर का उपयोग करना

एक्सेल आपको बुनियादी सांख्यिकीय विश्लेषण करने में मदद करने में महत्वपूर्ण भूमिका निभाता है: यह आपको लॉगरिदमिक प्रतिगमन की गणना सहित बुनियादी परीक्षण चलाने के लिए एक साफ और सिद्ध इंटरफ़ेस प्रदान करता है।

एक्सेल के साथ मुख्य समस्या यह है कि यह आपको समाधान चरण प्रदान नहीं करेगा। यह Copilot जैसे AI फ्रेमवर्क के आगमन से मदद कर सकता है, जो संभवतः गणना के वर्णनात्मक चरणों के साथ एक्सेल को संपन्न करेगा।

रिग्रेशन कैलकुलेटर के परिणामों को समझना और व्याख्या करना

किसी अन्य की तरह प्रतिगमन विश्लेषण , लघुगणकीय मामले में भी कोई अंतर नहीं है, क्योंकि आप मॉडल फिट सांख्यिकी पर एक नज़र डालेंगे, जैसे कि च-आँकड़े समग्र रूप से मॉडल की महत्ता का परीक्षण करना, तथा भविष्यवाणियों के व्यक्तिगत महत्व के लिए टी-सांख्यिकी .

इसके अलावा, आप संभवतः वर्णित भिन्नता और त्रुटि पर भी नज़र डालना चाहेंगे, और R^2 और समायोजित R^2 गुणांक , जो आपको मॉडल द्वारा आश्रित चर की व्याख्या की गई भिन्नता का अनुमान प्रदान करेगा।

लघुगणकीय प्रतिगमन उदाहरण

चरों पर विचार करें

एक्स: 1, 2, 3, 4, 5

और: 15, 25, 28, 29, 30

लघुगणकीय प्रतिगमन मॉडल का अनुमान लगाएं।

समाधान:

लघुगणकीय प्रतिगमन मॉडल के निर्माण के लिए X और Y चरों के लिए निम्नलिखित डेटा प्रदान किया गया है:

एक्स	और
1	15
2	25
3	28
4	29
5	30

स्वतंत्र चर जिसका हम उपयोग करेंगे वह X का प्राकृतिक लघुगणक है, और आश्रित चर Y है। इस सहायक प्रतिगमन के लिए प्रतिगमन गुणांक की गणना करने के लिए, निम्नलिखित तालिका का उपयोग करने की आवश्यकता है:

	एक्स	जेड = एलएन(एक्स)	और	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

उपरोक्त तालिका के आधार पर निम्नलिखित की गणना की जाती है:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

इसलिए, उपरोक्त गणनाओं के आधार पर, प्रतिगमन गुणांक (ढलान \(m\), और y-अवरोधन \(n\)) निम्नानुसार प्राप्त किए जाते हैं:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

इसलिए, हम पाते हैं कि प्रतिगमन समीकरण है:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

लेकिन चूंकि सहायक चर \(Z = \ln(X)\) है, हम निष्कर्ष निकालते हैं कि लघुगणकीय प्रतिगमन समीकरण है:

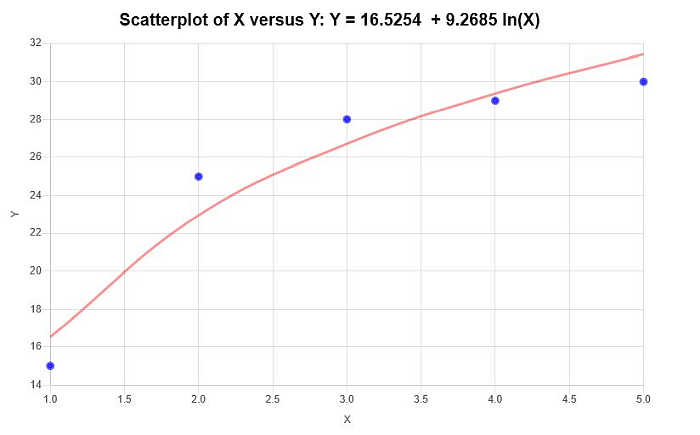
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

इसलिए, ऊपर दी गई जानकारी के आधार पर, निम्नलिखित स्कैटर प्लॉट और रिग्रेशन प्लॉट प्राप्त होते हैं:

अधिक सांख्यिकी कैलकुलेटर

इसमें आपकी भी रुचि हो सकती है घातांकीय प्रतिगमन की गणना , या किसी की सूक्ष्मताओं पर काम करना बहुपद प्रतिगमन ये सभी, देखे गए नमूना डेटा के व्यवहार के आधार पर, अलग-अलग संदर्भों में लागू होते हैं।

संभवतः, आप चाहेंगे एक तितर -बितर साजिश का निर्माण डेटा के अनुभवजन्य व्यवहार का आकलन करने के लिए, और यह पूर्व-मूल्यांकन करने के लिए कि क्या एक अलग प्रकार के प्रतिगमन के बजाय एक लघुगणकीय प्रतिगमन लागू होता है।