समाधानकर्ताओं बीजगणित

उलटा फ़ंक्शन ग्राफ़

निर्देश: आपके द्वारा प्रदान किए गए फ़ंक्शन के व्युत्क्रम फ़ंक्शन ग्राफ़ को खोजने के लिए इस ग्राफ़ का उपयोग करें, जो सभी चरण दिखाता है। कृपया नीचे दिए गए बॉक्स में वह फ़ंक्शन प्रदान करें जिसके लिए आप व्युत्क्रम फ़ंक्शन का ग्राफ़ प्राप्त करना चाहते हैं।

व्युत्क्रम फलनों के ग्राफ़ के बारे में अधिक जानकारी

यह कैलकुलेटर आपके द्वारा प्रदान किए गए व्युत्क्रम फ़ंक्शन का ग्राफ ढूंढने में आपकी सहायता करता है, बशर्ते कि फ़ंक्शन में व्युत्क्रम हो, जो हमेशा ऐसा नहीं होता है।

आप 'y = 2x - 1' प्रारूप में एक फ़ंक्शन प्रदान कर सकते हैं, या बस 'f(x) = (x-1)/(x-3)' या बस '(x-1)/( जैसा अभिव्यक्ति दे सकते हैं x-3)' फ़ंक्शन निर्दिष्ट करने के लिए।

एक बार जब आप एक वैध फ़ंक्शन प्रदान कर देते हैं, तो आप "गणना करें" बटन पर क्लिक कर सकते हैं, और आपको सभी चरण प्रदान किए जाएंगे व्युत्क्रम फलन की गणना , और यदि व्युत्क्रम मौजूद है, तो फ़ंक्शन और व्युत्क्रम के साथ एक ग्राफ़ दिखाया जाएगा।

ध्यान दें कि दिए गए फ़ंक्शन में व्युत्क्रम फ़ंक्शन होने के लिए, फ़ंक्शन को एक-से-एक होना आवश्यक है, जिसका अर्थ है कि फ़ंक्शन की सीमा में प्रत्येक मान की फ़ंक्शन के डोमेन में अधिकतम एक पूर्व-छवि होती है, और ठीक एक पूर्व-छवि में हम प्रभावी सीमा को प्रतिबंधित करते हैं।

कैसे जानें कि कोई फ़ंक्शन उलटा है या नहीं

किसी दिए गए फ़ंक्शन के लिए व्युत्क्रम का ग्राफ़ प्राप्त करने से पहले, आपको यह जानना होगा कि क्या फ़ंक्शन में कोई व्युत्क्रम है। व्युत्क्रम होने का मुख्य मानदंड एक-से-एक होना है, जिसका अर्थ है कि सीमा में एक मान में दो संबद्ध मान (प्रीइमेज) नहीं हो सकते हैं।

संभवतः छात्र 'इमेज' और 'प्रीइमेज' जैसे तकनीकी शब्दों का उपयोग नहीं करना पसंद करते हैं, और हालांकि ये फ़ंक्शन सिद्धांत में मुख्य अवधारणाएं हैं, इस मामले में हम यह आकलन करने के लिए एक सरल ग्राफ़िकल परीक्षण का उपयोग कर सकते हैं कि कोई फ़ंक्शन वन-टू-है या नहीं। एक, और इसलिए, यदि आप इसका व्युत्क्रम ढूंढ और रेखांकन कर सकते हैं।

क्षैतिज रेखा परीक्षण

क्षैतिज रेखा परीक्षण इंगित करता है कि किसी फ़ंक्शन को एक-से-एक होने के लिए, आपके द्वारा बनाई गई कोई भी क्षैतिज रेखा फ़ंक्शन के ग्राफ़ को अधिकतम एक बार पार करेगी। यदि आप एक क्षैतिज रेखा ढूंढने में सक्षम हैं जो दिए गए फ़ंक्शन के ग्राफ़ को एक से अधिक बार पार करती है, तो फ़ंक्शन एक-से-एक नहीं है।

उदाहरण के लिए, नीचे दिखाया गया फ़ंक्शन एक-से-एक है, क्योंकि इससे कोई फर्क नहीं पड़ता कि हम उस पर कौन सी क्षैतिज रेखा फेंकते हैं, यह फ़ंक्शन के ग्राफ़ को ठीक एक बार पार करेगा:

लेकिन फिर, अगला उदाहरण एक फ़ंक्शन दिखाता है जो एक-से-एक नहीं है, क्योंकि हम एक क्षैतिज रेखा देखते हैं जो फ़ंक्शन की रेखा को 2 बार (एक से अधिक बार) पार करती है:

क्षैतिज रेखा परीक्षण एक-से-एक उदाहरण नहीं है

व्युत्क्रम ग्राफ़ खोजने के चरण

स्टेप 1: दो सामान्य विधियाँ हैं: एक ग्राफिकल विधि है, और दूसरी विश्लेषणात्मक विधि है
चरण दो: ग्राफिकल विधि के लिए, आपको पहले क्षैतिज रेखा परीक्षण लागू करना होगा और सुनिश्चित करना होगा कि यह इसे पास कर लेता है, इसलिए यह एक-से-एक है, और व्युत्क्रम मौजूद है
चरण 3: फिर, आप ग्राफ़ में रेखा y = x खींचते हैं (एक सीधी रेखा जिसका कोण 45 है ^हे एक्स-अक्ष के संबंध में डिग्री
चरण 4: उसके बाद आप बस लाइन y = x को 'मिरर' के रूप में उपयोग करें और 'मिरर' के संबंध में मूल ग्राफ के बिंदुओं को प्रतिबिंबित करें। इस मिररिंग प्रक्रिया से प्राप्त ग्राफ व्युत्क्रम का ग्राफ है
चरण 5: विश्लेषणात्मक विधि के लिए, आपको पहले बीजगणितीय रूप से काम करना होगा उलटा खोजें : आप y = f(x) से शुरू करें और फिर y के लिए हल करें।
चरण 6: यदि केवल एक ही समाधान है, तो व्युत्क्रम मौजूद है और आप इसे x = g(y) लिखते हैं। परिवर्तनीय नामों को समायोजित करके, आप औपचारिक रूप से जी के संदर्भ में व्युत्क्रम फ़ंक्शन \(f^{-1}\) को परिभाषित करते हैं
चरण 7: अंत में, आप उस व्युत्क्रम का रेखांकन करते हैं जो आपको \(f^{-1}\) जैसा मिलता है एक फ़ंक्शन ग्राफ सामान्य रूप से

जब आपको ग्राफ़ को व्युत्क्रम खोजने की आवश्यकता होती है, तो ग्राफ़िकल और विश्लेषणात्मक दोनों तरीके ठीक होते हैं, केवल विश्लेषणात्मक विधि का लाभ होता है, जो यह है कि आप प्रक्रिया के साथ व्युत्क्रम फ़ंक्शन की गणना करते हैं, इसलिए अंत में आपको इसकी गणितीय अभिव्यक्ति प्राप्त होती है, न केवल इसका ग्राफ.

आप उलटा रेखांकन क्यों करेंगे?

आप ऐसा क्यों करेंगे इसके बहुत सारे कारण हैं। सबसे पहले, व्युत्क्रम फ़ंक्शन अपने आप में फ़ंक्शन सिद्धांत में एक बहुत ही महत्वपूर्ण अभिनेता है, क्योंकि एक फ़ंक्शन दिखाता है कि x से ay तक कैसे जाना है, इसलिए यह जानना स्वाभाविक है कि y से x तक जाने के लिए तंत्र क्या है, और यह बिल्कुल वही है जो व्युत्क्रम फ़ंक्शन आपको प्रदान करता है।

तो, कोई एक फ़ंक्शन को बिंदु "X" से बिंदु "Y" तक एक-तरफ़ा मानचित्र के रूप में सोच सकता है, और व्युत्क्रम फ़ंक्शन की गणना करना "Y" से "X" तक जाने के लिए मानचित्र को स्पष्ट रूप से परिभाषित करने जैसा है।

और फिर व्युत्क्रम का ग्राफ़ आपको उस व्युत्क्रम फलन के बारे में बहुत सारी जानकारी बताएगा: क्या यह नीचे की ओर जाता है, यह कैसे व्यवहार करता है।

यह व्युत्क्रम ग्राफ फ़ंक्शन कैलकुलेटर मेरी कैसे मदद करता है?

सबसे पहले, यह कैलकुलेटर विश्लेषणात्मक विधि का उपयोग करके यह देखने के लिए फ़ंक्शन का विश्लेषण करेगा कि क्या यह उलटा है, और यदि ऐसा उलटा ढूंढना संभव है, तो यह आपके लिए इसे ग्राफ़ करेगा।

व्युत्क्रम ढूँढना शामिल है एक समीकरण हल करना , जो तब तक आसान काम नहीं है जब तक कि आप इससे निपट न लें रेखीय समीकरण या बहुपद समीकरण , लेकिन इसके अलावा, प्रक्रिया बहुत जटिल या असंभव भी हो सकती है।

अन्य कैलकुलेटर भी इसी तरह की प्रक्रिया कर सकते हैं, लेकिन इसका एक फायदा यह भी है यह कैलकुलेटर बात यह है कि यह जहां संभव हो, विस्तृत विवरण के साथ प्रक्रिया के सभी चरण प्रदान करता है।

उदाहरण: व्युत्क्रम का ग्राफ ढूँढना

इसका व्युत्क्रम ग्राफ़ बनाएं: \( y = \frac{2}{3} x - \frac{5}{6}\)

समाधान:

हमें निम्नलिखित फ़ंक्शन प्रदान किया गया है:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

फिर, दिए गए फ़ंक्शन का व्युत्क्रम खोजने के लिए, हमें \(x\) को हल करना होगा और यह निर्धारित करना होगा कि कोई समाधान है या नहीं। प्रारंभिक समीकरण है

\[y=\frac{2}{3}x-\frac{5}{6}\]

चरण 0: इस मामले में, हमें पहले दिए गए रैखिक समीकरण को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरण अपनाते हैं:

\( \displaystyle y-\left(\frac{2}{3}x-\frac{5}{6}\right) = 0\)

Multiplying by -1: \(-\left(\frac{-5}{6}+\frac{2}{3}x\right) = \frac{5}{6}-\frac{2}{3}x\)

\( \displaystyle \Rightarrow \,\, \,\,\)

\(\displaystyle y+\frac{5}{6}-\frac{2}{3}x = 0\)

रैखिक समीकरण को हल करना

बाएं हाथ की तरफ \(x\) और \(y\) और दाहिने हाथ की तरफ स्थिर

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

अब, \(x\)के लिए हल करना, समीकरण के दोनों किनारों को \(-\frac{2}{3}\)द्वारा विभाजित करके, निम्नलिखित प्राप्त किया गया है

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

और सरलीकरण करते हुए हम अंत में निम्नलिखित प्राप्त करते हैं

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

इसलिए, दिए गए रैखिक समीकरण के लिए \(y\) को हल करने पर \(x = \frac{3}{2}y+\frac{5}{4}\) प्राप्त होता है।

इसलिए, और चूँकि \(x\) को हल करते समय हमें एक समाधान मिलता है और यह केवल एक ही समाधान है, हमने व्युत्क्रम पाया है।

व्युत्क्रम फलन मिला

ऊपर दिखाए गए कार्य के आधार पर, यह निष्कर्ष निकाला जा सकता है कि उलटा कार्य है:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

व्युत्क्रम फ़ंक्शन को ग्राफ़िक रूप से निम्नानुसार दिखाया जा सकता है:

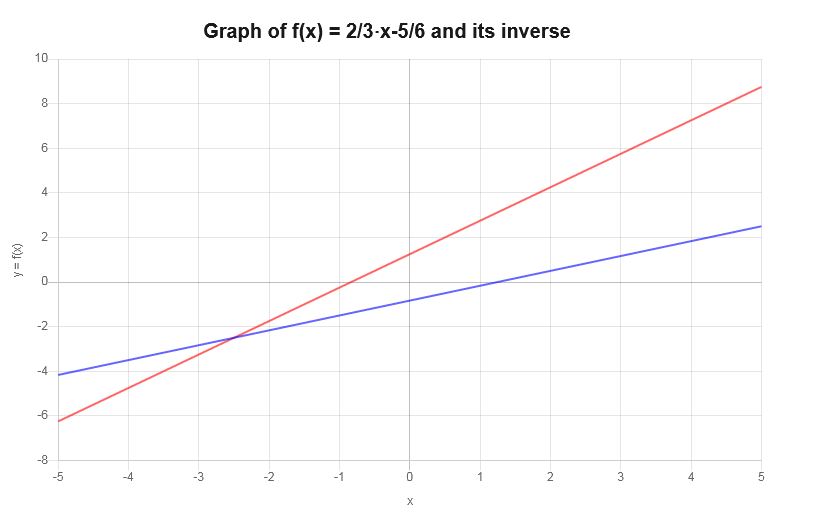
उदाहरण: अधिक व्युत्क्रम ग्राफ़

क्या आप इसका व्युत्क्रम ग्राफ़ ढूंढ सकते हैं: \(y = x^2\)

समाधान: नहीं, हम \(y = x^2\) का व्युत्क्रम ग्राफ़ नहीं ढूंढ सकते, क्योंकि यह फ़ंक्शन क्षैतिज रेखा परीक्षण पास नहीं करता है। इसे देखने का दूसरा तरीका यह है कि \(x\) को हल करने पर हमें \(x = \pm \sqrt y\) मिलता है, और चूँकि हमें दो समाधान मिलते हैं, तो कोई व्युत्क्रम नहीं होता है, और परिणामस्वरूप, कोई व्युत्क्रम ग्राफ नहीं होता है।

अधिक फ़ंक्शन कैलकुलेटर

फ़ंक्शंस और किसी भी प्रकार के फ़ंक्शन संचालन वास्तव में बीजगणित और कैलकुलस का केंद्र हैं। एक अच्छा समारोह कैलकुलेटर किसी फ़ंक्शन को उसकी सरलतम अभिव्यक्ति तक सीमित करने के मामले में आपका जीवन आसान हो जाएगा।

फिर, आपका भला होगा फ़ंक्शन रेखांकन उपकरण किसी फ़ंक्शन के ग्राफ़िकल गुणों पर एक त्वरित नज़र डालने के लिए। किसी फ़ंक्शन का ग्राफ़ देखने से आप उसके बीजगणितीय अभिव्यक्ति को देखने से पहले ही उसके व्यवहार के बारे में बहुत कुछ बता सकते हैं।

फिर आपके पास अधिक उन्नत ऑपरेशन हैं जैसे कि व्युत्पन्न ढूंढना, जिसके लिए यह विभेदन कैलकुलेटर यह आपके काम आएगा, क्योंकि यह आपको प्रक्रिया के सभी चरण दिखाता है। जैसा कि अपेक्षित था, व्युत्क्रम फलन के व्युत्पन्न का मूल फलन के व्युत्पन्न के साथ एक दिलचस्प संबंध है।