Slope-Intercept Form Calculator
Instructions: Use this calculator to get the equation of the line in slope-intercept form, showing all the calculations, step-by-step. For that, you need to provide information about the line you need to get in slope-intercept form.
You have different options to provide information about the line. You can provide: (1) both the slope and the y-intercept, (2) you can provide any linear equation (ex: \(2x + \frac{1}{5}y = 3 + 2x\)), (3) you can provide the slope and a point that the line passes through, or (4) you can provide two points where the line passes through.
More about this line in slope-intercept form calculator
This slope-intercept equation calculator will allow you to provide information of a linear equation in one of four ways, and then it will show how to put it into slope-intercept form, with the following formula:
\[y = ax + b\]where a is the slope of the line, and b is the y-intercept, and your objective to find both. More about that below.
How do you define the equation of the line in this calculator
First, you need to provide information to specify the equation. There are several ways to define a linear equation. One way is to simply to type out a valid linear equation directly.
But other times, depending on what type of information you have been provided with, you may have the slope and y-intercept (which together univocally define a line) or also you can provide the slope of the line and one point it passes through.
Ultimately, you may have two points you know the line passes through, which also would define one and one line only.
So based on the information you have, you will need to decide what option do you use to initially identify your line.
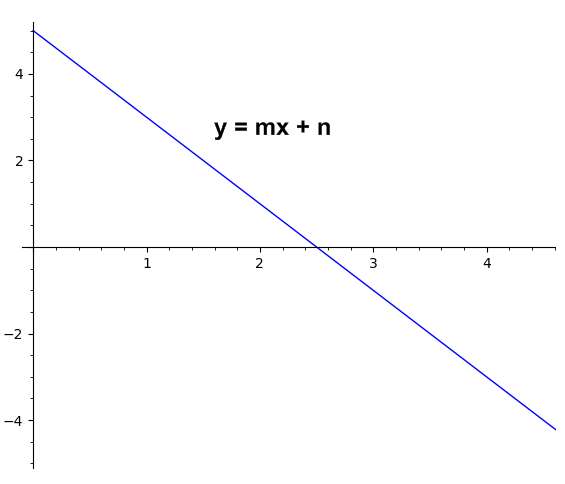
How do you represent a line in slope-intercept format?
A linear equation is said to be in slope-intercept form if it has the following structure:
\[y = m x + n\]Perhaps you have seen it written like \(y = a + b x\), but that is exactly the same: We have the dependent variable (\(y\)) on one side, and we have a constant plus another constant (which could be negative) multiplying the independent variable (\(x\)).
How do you arrive to the slope-intercept on a calculator?
With this solver/calculator, all you need to do is provide information with which you can identify the line you are working with, using one of the four different options.
Once you have provided the initial information, the procedure to arrive to the slope-intercept form will depend on the way the line was initially constructed, but the idea is that we solve for \(y\).
Why is the slope-intercept form of a line very commonly used
The slope-intercept of a line is very commonly used because it gives a very intuitive and graphical depiction what the line does. With the y-intercept we know where the line intersects the y-axis, and with the slope we know a degree of the inclination of the line.
A negative slope indicates a declining line, and a positive slope indicates an ascending line. When the slope is zero, then the line is horizontal
Also, putting the equation of a line in slope-intercept form allows for easy solution of simultaneous linear equations.
Can this solver go from standard form to slope intercept form?
Absolutely. If you have an equation in standard form, all you have to do is type the equation, click "Calculate" and the solver will show, step-by-step, how to get to slope-intercept form.

Example: Slope-intercept calculation
Assume that you have a line in standard form \( \frac{1}{3} x + \frac{4}{5} y = 2\). Find the slope-intercept form.
Answer:
We have been provided with the following equation:
\[\displaystyle \frac{1}{3}x+\frac{4}{5}y=2\]Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get
\[\displaystyle \frac{4}{5}y = -\frac{1}{3}x +2\]Finally, solving for \(y\), the following is obtained
\[\displaystyle y=\frac{-\frac{1}{3}}{\frac{4}{5}}x+\frac{2}{\frac{4}{5}}\]and simplifying all the terms that need simplification, we finally get the following
\[\displaystyle y=-\frac{5}{12}x+\frac{5}{2}\]Conclusion: Based on the data provided, we conclude that the equation of the line in slope-intercept form is \(\displaystyle y=-\frac{5}{12}x+\frac{5}{2}\), with a slope of \(\displaystyle m = -\frac{5}{12}\) and y-intercept of \(\displaystyle n = \frac{5}{2}\).