وظائف فردية
تعليمات: استخدم هذه الآلة الحاسبة لاختبار دالة واحد لواحد, مع عرض جميع الخطوات. يرجى كتابة الوظيفة التي تريد التحقق منها في المربع أدناه.
وظائف فردية
ستسمح لك هذه الآلة الحاسبة بتقييم ما إذا كانت الدالة واحدة لواحد أم لا, مع عرض جميع الخطوات. أول شيء عليك القيام به هو توفير الوظيفة. يمكن أن يكون هذا شيئًا بسيطًا أو خطيًا أو تربيعيًا مثل 'y = x^2 - 1', أو يمكنك أن تقرر الانتقال إلى وظيفة عقلانية مثل 'f(x) = (x-1)/(x+3)'.
وبعد ذلك, نحن راضون عما قدمته وتأكدت من صلاحية الوظيفة, قم بالضغط على زر "احسب", حتى تحصل على جميع خطوات العملية الموضحة لك.
يعد مفهوم الدالة واحد لواحد مفهومًا مهمًا جدًا في الجبر وحساب التفاضل والتكامل. هناك العديد من الطرق البسيطة لاختبار واحد لواحد, إحداها هي اختبار الخط الأفقي , ولكن نظرًا لطبيعتها, فمن الأسهل استخدامها لدحض أن الدالة هي واحد لواحد. لإثبات أن الدالة واحد لواحد, نحتاج إلى حل المعادلة , عملية تحليلية.

ما هي عملية واحد لواحد
ببساطة, دالة واحد لواحد أو دالة حقنية هي التي بالنسبة لاثنين مختلفين من \(x_1\) و \(x_2\), تختلف قيم صورهما من خلال \(f(x)\), وهو ما يعني رياضيًا
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]يحب بعض المدرسين كتابتها بشكل مختلف قليلًا, ولكن بطريقة متكافئة: الوظيفة فردية إذا
\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]هذا يعني بطريقة معقدة إلى حد ما أنه إذا كان الرسم البياني للدالة يعبر نفس القيمة (خط أفقي), فإن ذلك يحدث فقط عندما تكون النقطة هي نفسها. إذن, كل ما تقوله هو أنه لا توجد نقطتان مختلفتان يعبرهما خط أفقي. لذلك, أنت مجرد تكرار اختبار الخط الأفقي .
كيفية التحقق مما إذا كانت الدالة فردية أم لا
- الخطوة 1: ابدأ بالدالة الأصلية f(x), وقم بتعيين المعادلة y = f(x)
- الخطوة 2: محاولة حل لx
- الخطوه 3: إذا وجدت أكثر من حل, فالدالة ليست واحد لواحد, وإذا كان لها حل واحد أو لا يوجد حل, فالدالة هي واحد لواحد
عادةً, ستقوم ببعض الفحص الأساسي للتأكد من أن هذه الوظيفة ليست وظيفة واحد لواحد, ربما لأنه يمكنك بسهولة العثور على خط أفقي لفشل HLT.
بعد ذلك, سوف تبحث عن بعض الخصائص المرئية الأساسية: هل الدالة تتزايد دائمًا (ثم تكون واحدًا لواحد), وينطبق الشيء نفسه على الحالة التي تتناقص فيها الدالة دائمًا.
كيف يرتبط واحد لواحد بإيجاد المعكوس
بعبارات بسيطة, من أجل العثور على معكوس الدالة, يجب أن تكون الدالة واحد لواحد, على الأقل في مجال فرعي معين. في كثير من الأحيان نقوم بتقييد المجال بحيث ننشئ دالة 1 إلى 1 في مجال مقيد, بحيث لا تكون 1 إلى 1 بخلاف ذلك.
على سبيل المثال, \(f(x) = x^2\) ليس واحدًا لواحد بشكل عام. لماذا, لأنه يمكنك أن تأخذ نقطتين مختلفتين \(x_1 = -1\) و \(x_2 = 1\) وتجد أن \(f(x_1) = (-1)^2 = 1\) و \(f(1) = 1^2 = 1\), مما يعني أن الخاصية (التوصيف الفردي)
\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]غير راض. الآن, بدلاً من النظر إلى السطر الحقيقي الكامل \(\R\), نأخذ في الاعتبار القيم الموجبة فقط, فيمكننا أن نستنتج أن الدالة هي واحد لواحد على القيم الحقيقية الموجبة (تلميح: في هذا المجال الفرعي, الدالة تتزايد)

هل هناك صيغة لتقييم ما إذا كانت الوظيفة واحدة لواحد؟
للأسف لا. أعني أنه يمكن للمرء أن يفكر في \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \), باعتبارها صيغة واحد لواحد, ولكن هذا شرط منطقي أكثر من كونه صيغة.
على الرغم من ذلك, هناك إجراء عام وواسع جدًا يُستخدم لاختبار ما إذا كانت الوظيفة فردية أم لا, وهو ما تراه موضحًا أعلاه. لا توجد "صيغة واحد لواحد". إذا أردنا التسوية بواحد, فيجب أن يكون y = f(x).
ونحن نحل فقط لـ x. لاأكثر ولا أقل. في النهاية, سيعتمد الأمر على ما يدور حوله f(x). دالة معقدة للغاية ومعقدة قد تشكل الكثير من الصعوبات التي يتعين حلها, وربما تحتاج إلى آلة حاسبة دالة لها, وحتى مع حاسبة الدوال قد تفشل.
ربما تفكر لماذا ذلك؟؟ السبب هو أننا, في قلب الأمر, لا نملك تقنيات لحل جميع المعادلات. نحن نفعل ما في وسعنا مع نوع معين من المعادلات, ولكننا بعيدون عن معرفة الطريقة الدقيقة لحل جميع المعادلات.

مثال: دالة واحد لواحد
هل الوظيفة التالية حقنية: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)
حل:
لقد تم تزويدنا بالوظيفة التالية:
\[f(x) = \frac{1}{4} x + \frac{5}{4}\]بعد ذلك, من أجل تقييم ما إذا كانت الدالة المعطاة واحدة لواحد أم لا, نحتاج إلى حل \(x\) وتحديد ما إذا كان لا يوجد حل, أو حل واحد, أو حلول متعددة. معادلة البداية هي
\[y=\frac{1}{4}x+\frac{5}{4}\]وضع \(x\) على الجانب الأيسر و \(y\) والثابت على الجانب الأيمن الذي نحصل عليه
\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]الآن , حل \(x\), من خلال تقسيم جانبي المعادلة بواسطة \(-\frac{1}{4}\), يتم الحصول على ما يلي
\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]وتبسيط نحصل أخيرًا على ما يلي
\[\displaystyle x=4y-5\]لذلك, فإن حل \(x\) لمعادلة خطية معينة يؤدي إلى \(x=4y-5\) وهو حل حقيقي واحد فقط, وبالتالي فإن الدالة المعطاة هي واحد لواحد.
خاتمة
بناءً على ما تم العثور عليه في القسم السابق, يمكن استنتاج أن الوظيفة المعطاة هي واحد لواحد.
بيانياً:
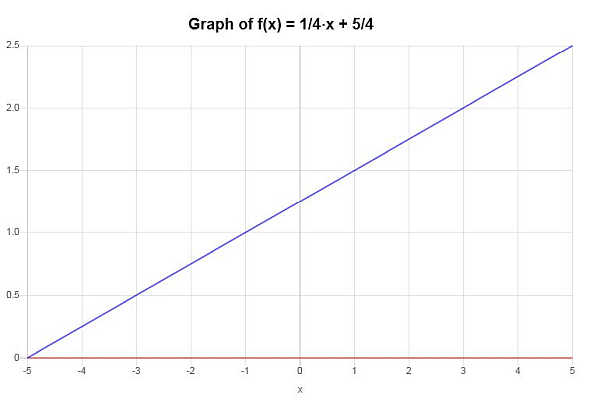
مثال: وظيفة 1 إلى 1
أثبت أو دحض أن الدالة التالية واحدة لواحد: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)
حل: من أجل تقييم ما إذا كانت الدالة المعطاة واحدة لواحد أم لا, نحتاج إلى حل \(x\) وتحديد ما إذا كان لا يوجد حل, أو حل واحد, أو حلول متعددة. معادلة البداية التي نحتاج إلى استخدامها هي:
\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]خطوة أولية: في هذه الحالة, نحتاج أولاً إلى تبسيط المعادلة المعطاة, وللقيام بذلك, نقوم بخطوات التبسيط التالية:
إذن الحلول هي:
\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]حالة واحد لواحد
بناءً على العمل الموضح أعلاه, يمكن استنتاج أن الدالة المعطاة ليست واحد لواحد, لأنها لم تنجح في اختبار الخط الأفقي, على سبيل المثال الخط \(y = 0\) هو خط أفقي يتقاطع مع الدالة المحددة أكثر من مرة.
بيانيا, يتم تصوير الوضع على النحو التالي:
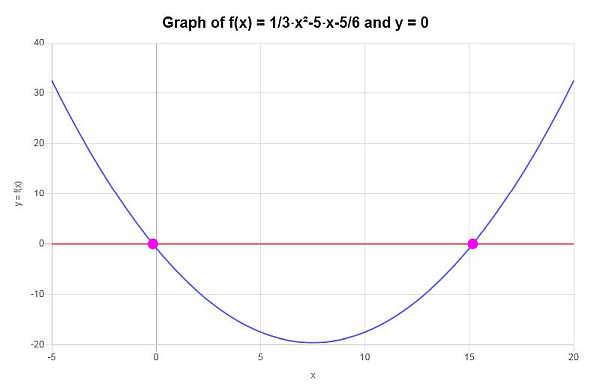
الآلات الحاسبة الجبر أكثر إثارة للاهتمام
عادة ما يتم اعتبار مفهوم الوظائف 1 إلى 1 أمرا مفروغا منه, لكنه مفهوم مهم للغاية, وأود أن أقول أنه بالغ الأهمية. وذلك لأن مفهوم واحد لواحد يرتبط ارتباطًا وثيقًا بفكرة الوظيفة الرتيبة (الوظائف المتزايدة أو المتناقصة), كما أنه مرتبط ارتباطًا وثيقًا بالوظيفة الرتيبة حساب الدالة العكسية والرسم البياني لها.
ومع ذلك, في كثير من الأحيان يكون من الصعب تجاوز الغابة خلف الأشجار, حيث أن معظم مفاهيم الجبر وحساب التفاضل والتكامل لها روابط وثيقة مع بعضها البعض. تحليل الوظيفة هو أحد الأشياء التي ستفعلها طوال الوقت, لذلك من الجيد أن تكتسب المهارات اللازمة لتصبح جيدًا في ذلك.






