关于反函数图形的更多信息

该计算器可以帮助您找到所提供反函数的图形,前提是该函数具有反函数,但情况并非总是如此。

您可以提供格式为 "y = 2x-1 "的函数,也可以直接给出 "f(x) = (x-1)/(x-3) "或"(x-1)/(x-3) "这样的表达式来指定函数。

提供有效函数后,您可以点击 "计算 "按钮,然后就会看到 "计算 "的所有步骤。 反函数计算 如果存在反函数,则会显示出包含函数和反函数的图形。

请注意,要使给定函数具有反函数,函数必须是一一对应的,这意味着函数范围内的每个值在函数域中最多有一个前像,而在我们限制的有效范围内恰好有一个前像。

如何知道函数是否可反转

在绘制给定函数的逆定理图之前,需要先了解该函数是否有逆定理。是否有反函数的主要标准是一一对应,即范围内的一个值不能有两个相关值（前像）。

学生们可能不喜欢使用 "图像 "和 "前像 "等专业术语,虽然这些都是函数论中的核心概念,但在这种情况下,我们可以使用简单的图形测试来评估函数是否一一对应,从而评估你是否能找到并绘制出它的反函数。

水平线测试

水平线测试表明,要使一个函数是一一对应的,那么您所构造的任何水平线最多只能与该函数的图形相交一次。如果您能找到一条与给定函数的图形相交不止一次的水平线,那么该函数就不是一一对应的。

例如,下图所示的函数是一一对应的,因为无论我们向它抛出哪条水平线,它都会恰好与函数的图形相交一次：

但是,下一个示例显示的函数不是一一对应的,因为我们看到一条水平线与函数的直线相交 2 次（不止一次）：

求逆图形的步骤

• 步骤1： 常用的方法有两种：一种是图形法,另一种是分析法
• 第2步： 对于图解法,您需要首先应用水平线检验,并确保它通过了水平线检验,因此它是一一对应的,并且存在反比例
• 第3步： 然后,在图形中画出 y = x 的直线（角度为 45°的直线）。 ^o 相对于 x 轴的度数
• 第4步： 之后,您只需将直线 y = x 作为 "镜像",并将原始图形的各点相对于 "镜像 "进行反射。通过镜像处理得到的图形就是反比例的图形
• 第5步： 对于分析方法,您需要首先对以下内容进行代数处理 求逆 :从 y = f(x) 开始,然后求解 y。
• 第6步。 如果只有一个解,那么反函数就存在,可以写成 x = g(y)。调整变量名后,用 g 正式定义反函数 \(f^{-1}\)
• 第7步。 最后,将找到的倒数 \(f^{-1}\) 绘制成图形,就像绘制 绘制函数图 通常

当你需要求一个反函数的图形时,图形法和解析法都可以,只有解析法有一个优点,那就是你可以在计算过程中计算出反函数,所以你最终得到的是它的数学表达式,而不仅仅是它的图形。

为什么要绘制逆

为什么要这么做,原因有很多。首先,反函数本身就是函数论中一个非常重要的角色,因为一个函数展示了如何从 x 到 y,所以自然而然就会想知道从 y 到 x 的机制是什么,而这正是反函数所提供的。

因此,我们可以把函数看作是从点 "X "到点 "Y "的单向映射,而计算反函数就好比明确定义一个从 "Y "到 "X "的映射。

然后,反函数的图形会告诉你很多关于反函数的信息：它是否上升,它的表现如何。

这款反比图函数计算器如何帮助我？

首先,这款计算器会使用解析法分析函数是否可逆,如果可以找到可逆函数,它还会为您绘制曲线图。

求逆数涉及 解方程 除非你面对的是 线性方程组 或 多项式方程 除此之外,这个过程可能非常复杂,甚至不可能完成。

其他计算器可能也会进行类似的处理,但它的优势之一是 这个计算器 因为它提供了整个过程的所有步骤,并在可能的情况下提供了详细的解释。

例题寻找倒数的图形

绘制：\( y = \frac{2}{3} x - \frac{5}{6}\)

解决方案：

我们获得了以下功能：

\[ y = \frac{2}{3} x - \frac{5}{6}\]

然后,为了找到给定函数的逆,我们需要求解 \(x\),并确定是否存在解。起始方程为

\[y=\frac{2}{3}x-\frac{5}{6}\]

第0步。 在这种情况下,我们首先需要对给定的线性方程进行化简,为此,我们要执行以下化简步骤：

解线性方程

将 \(x\) 放在左侧,将 \(y\) 和常数放在右侧,我们得到

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

现在,用方程两边除以 \(-\frac{2}{3}\),求解 \(x\),得到如下结果

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

并简化我们最终得到以下

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

因此,对给定的线性方程求解 \(y\) 就会得到 \(x = \frac{3}{2}y+\frac{5}{4}\)。

因此,在求解 \(x\) 时,我们找到了一个解,而且只有一个解,所以我们找到了逆。

发现反函数

根据上述工作,可以得出反函数为：

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

反函数的图示如下

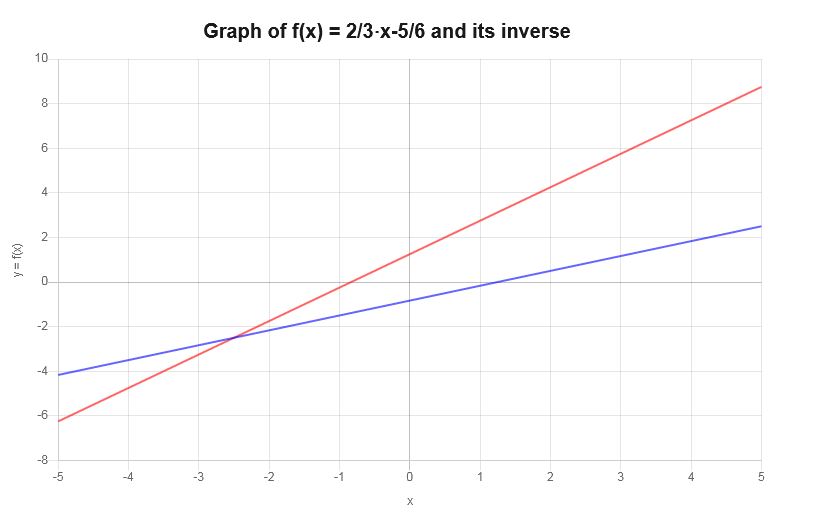
举例说明：更多逆变图形

你能找出\(y = x^2\)

解决方案： 不,我们无法找到 \(y = x^2\) 的逆图形,因为这个函数没有通过水平线检验。另一种看法是,当求解 \(x\) 时,我们得到 \(x = \pm \sqrt y\),由于我们找到了两个解,因此没有逆,也就没有逆图形。

更多函数计算器

函数和任何类型的函数运算都是代数和微积分的核心。一个好的 功能计算器 会让你更轻松地将函数简化为最简单的表达式。

然后,你就可以 函数图形工具 以快速了解函数的图形属性。即使在查看函数的代数表达式之前,通过查看函数的图形也能了解其行为。

然后是更高级的操作,例如求导数。 差异化计算器 就会派上用场,因为它会向你展示这一过程的所有步骤。不出所料,反函数的导数与原函数的导数有着有趣的联系。