Решатель квадратных уравнений

Этот калькулятор позволит вам вычислить квадратное уравнение который вы предоставите, показывая все шаги. Все, что вам нужно сделать, это предоставить действительное квадратное уравнение.

Это может быть что-то, что уже упрощено и готово к решению, как x^2 + 3x + 5 = 0, вы можете предоставить что-то не легко упрощенное, как 3x^2 - 4x + 5/3 = x^2 +1/3x -1, например.

Как только вы введете правильное квадратное уравнение, все, что вам нужно сделать, это нажать кнопку "Вычислить", и вам будут представлены все шаги процесса вычисления корни квадратного уравнения который предоставляется.

Обычно для вычисления квадратных уравнений используется квадратичная формула, но это не единственный способ, как мы увидим в следующих разделах.

Как вычислить квадратное уравнение?

Существует несколько стратегий решения квадратных уравнений. Наиболее часто используемая из них - это использование метода квадратичная формула . Также вы можете решить квадрат , или вы можете решить с помощью квадратичная факторизация .

Каковы этапы вычисления квадратных уравнений с помощью квадратичной формулы?

• Шаг 1: Определите квадратное уравнение, которое вы хотите вычислить
• Шаг 2: Убедитесь, что уравнение полностью упрощено, иначе продолжайте упрощение, пока не получите уравнение вида ax² + bx + c = 0
• Шаг 3: После приведения уравнения к упрощенной форме можно воспользоваться квадратичной формулой: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Возможно, использование формулы квадратного уравнения является наиболее практичным способом нахождения корней квадратного уравнения, но есть и другие причины, по которым вы можете использовать другие методы.

Как решить квадратное уравнение путем возведения в квадрат?

Вторым наиболее распространенным способом решения квадратного уравнения является использование техники квадрат . На самом деле не существует формулы для завершения квадратов (хотя технически она есть, основанная на решениях квадратного уравнения), и это скорее процесс.

Каковы шаги по заполнению квадратов

• Шаг 1: Определите квадратное уравнение, которое вы хотите решить
• Шаг 2: Вам необходимо убедиться, что уравнение полностью упрощено, и что у вас есть уравнение вида ax² + bx + c = 0
• Шаг 3: Добавьте и вычтите подходящий член (в данном случае, (b/(2a))², чтобы заставить члены квадрата бинома

Идея заставить появиться термин вида (x + "что-то)², который является конечной целью заполнения квадратов.

Почему вы используете квадратичные уравнения?

Квадратичные уравнения постоянно появляются в приложениях к алгебре в виде словесных задач. Решение квадратных уравнений - один из основных базовых навыков, которые вам необходимо приобрести.

Затем, в таких областях, как Calculus, при вычислении задач максимизации и минимизации, вам потребуется хорошее знакомство со всеми типами квадратичных уравнений.

Пример: решение квадратного уравнения

Решите следующее квадратное уравнение, используя формулу <

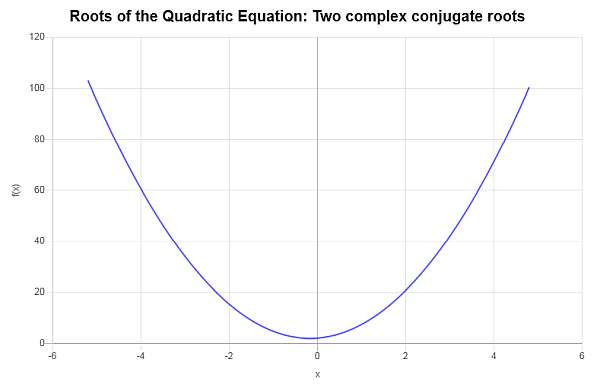
Отвечать: Нам необходимо решить следующее заданное квадратное уравнение \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Для квадратного уравнения вида \(a x^2 + bx + c = 0\) корни вычисляются по следующей формуле:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В данном случае мы имеем, что уравнение, которое нам нужно решить, имеет вид \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), из чего следует, что соответствующие коэффициенты имеют вид:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Сначала мы вычислим дискриминант, чтобы оценить природу корней. Дискриминант вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Поскольку в данном случае дискриминант \(\Delta = \displaystyle -\frac{272}{9} < 0\) отрицательный, мы знаем, что данное уравнение имеет два различных сопряженных комплексных корня.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

итак, мы выяснили, что:

\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Поэтому данное уравнение \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) имеет два различных сопряженных комплексных корня, которыми являются \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) и \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Графически:

Пример: корень квадратного уравнения

Найдите корни следующего квадратного уравнения, заполнив квадраты \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

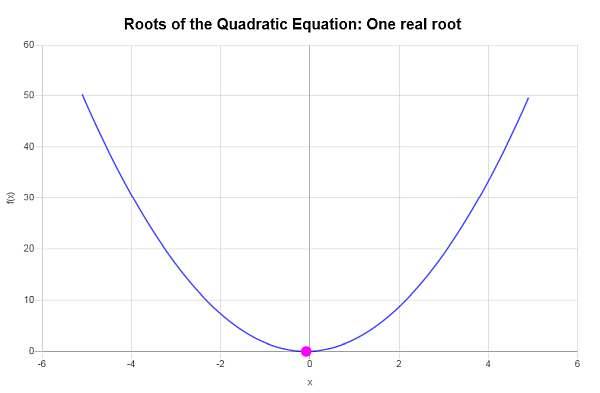
Отвечать: В данном случае мы имеем, что уравнение, которое нам нужно решить, имеет вид \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), из чего следует, что соответствующие коэффициенты имеют вид:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

Дискриминация вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Поскольку в этом случае дискриминант \(\Delta = \displaystyle 0 = 0\) равен нулю, мы знаем, что уравнение имеет только один действительный корень.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

итак, мы выяснили, что:

\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Поэтому данное уравнение \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) имеет только один вещественный корень, который равен \(x = \displaystyle -\frac{1}{12}\).

Графически:

Пример: вычисление корней уравнения

Решите следующие задачи: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

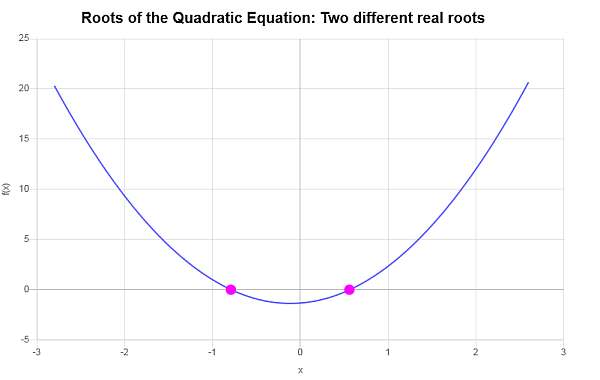
Отвечать: Для данного примера уравнение, которое нам нужно решить, имеет вид \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), тогда соответствующие коэффициенты будут:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

В этом случае дискриминация вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Поскольку дискриминант \(\Delta = \displaystyle \frac{148}{9} > 0\) положительный, мы знаем, что уравнение будет иметь два различных вещественных корня.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

итак, мы выяснили, что:

\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Поэтому данное уравнение \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) имеет два различных вещественных корня, которыми являются \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) и \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Графически:

Другие полезные квадратичные калькуляторы

Как мы уже видели в этом учебнике, квадрат играет фундаментальную роль в вычислении квадратных уравнений. Кроме того, вы можете использовать калькулятор дискриминанта оценить характер корней (два действительных корня, один действительный корень или два комплексных корня) без решения уравнения.

Вы также можете использовать это Вершинный калькулятор для нахождения координат вершины квадратного уравнения, и найти ось симметрии параболы . Также вы можете изучить следующее квадратичная факторизация инструмент для изучения еще одного способа вычисления квадратных уравнений.