Logarithmic Regression
Instructions: Use this calculator to estimate a logarithmic regression model based on X and Y data. Just type or paste your data in the spreadsheet below.
How a Logarithmic Regression Calculator Works
This calculator will allow you estimate a logarithmic regression for sample data you provide in the corresponding data input spreadsheet.
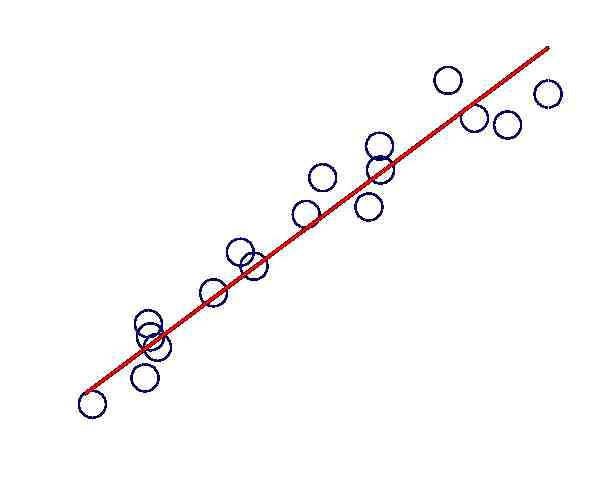
When valid data are provided (in this case, the X variable can only take positive values), after you click on "Calculate", you will get a run of the steps involved in the process as well as with a scatterplot that will show the quality of the fit.
Notice that when the data are dimensionally valid, you can always run a logarithmic regression, but that does not mean that the results will be of good quality, at least in terms of the fit.

Tools and Calculators for Logarithmic Regression
There are different tools you can use to estimate your logarithmic regression. In theory, you can go by doing things manually, using a log transformation using a regular calculator perhaps (even those that come with your phone), and then use an auxiliary least squares equation to find the log model, which is
\[ Y = a + b \ln(X) + \varepsilon \]Certainly, the doing it by hand approach could be tedious and error prone, to say the least. That is why it is a very good option to use this logarithmic regression calculator , because it does all the work for you and it shows you all the steps
There are other tools like mobile phone apps that are supposed to do all types of regression, but you will need to try and see because that could be hit or miss kinda situation.
Steps for Running a Logarithmic Regression
- Step 1: List the independent variable (X) and dependent variable (Y) clearly, and make sure that both variables have the same sample size
- Step 2: Make sure your values of X are positive, otherwise you cannot run the regression
- Step 3: Construct a new independent variable X* = ln(X) by applying the natural log transformation
- Step 4: You now run a regular linear regression analysis for X* versus Y
One thing to keep in mind is that it is completely advisable to use a calculator or software so to get diagnostic statistics that will help you assess whether it makes sense or not to use the logarithmic regression model .
Using Excel vs Dedicated Logarithmic Regression Calculators
Excel plays an important role at helping you conduct basic statistical analysis: it provides you with a clean and proven interface for running basic tests, including the calculation of logarithmic regression.
The main problem with Excel is that it won't provide you with the solutions step. This may help with the advent of AI frameworks such as Copilot, which would likely endow Excel with descriptive steps of the calculation.
Understanding and Interpreting Regression Calculator Results
Like any other regression analysis , for the logarithmic case is no different in that you will take a look at model fit statistics, such as the F-statistics to test for significance of the model overall, and t-statistics for individual significance of predictors .
Also, you will likely want to take a look at explained variation and error, and the R^2 and Adjusted R^2 coefficients , which will provide you with estimates of the explained variation of the dependent variable by the model.
Logarithmic Regression Examples
Consider the variables
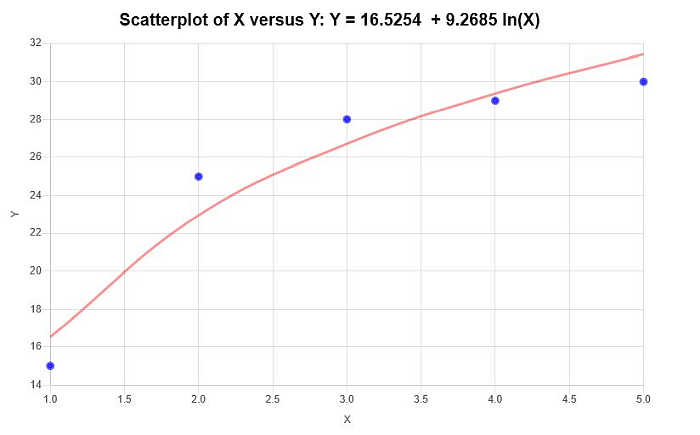
X: 1, 2, 3, 4, 5
Y: 15, 25, 28, 29, 30
Estimate a logarithmic regression model.
Solution:
The following data for the X and Y variables are provided to construct a logarithmic regression model:
| X | Y |
| 1 | 15 |
| 2 | 25 |
| 3 | 28 |
| 4 | 29 |
| 5 | 30 |
The independent variable that we will use is the natural log of X, and the dependent variable is Y. In order to compute the regression coefficients for this auxiliary regression, the following table needs to be used:
| X | Z = ln(X) | Y | \(Z \cdot Y\) | \(Z^2\) | \(Y^2\) | |
| 1 | 0 | 15 | 0 | 0 | 225 | |
| 2 | 0.69 | 25 | 17.33 | 0.48 | 625 | |
| 3 | 1.1 | 28 | 30.76 | 1.21 | 784 | |
| 4 | 1.39 | 29 | 40.2 | 1.92 | 841 | |
| 5 | 1.61 | 30 | 48.28 | 2.59 | 900 | |
| Sum = | 15 | 4.79 | 127 | 136.58 | 6.2 | 3375 |
Based on the above table, the following is calculated:
\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]Therefore, based on the above calculations, the regression coefficients (the slope \(m\), and the y-intercept \(n\)) are obtained as follows:
\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]Therefore, we find that the regression equation is:
\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]But since the auxiliary variable \(Z = \ln(X)\), we conclude that the logarithmic regression equation is:
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]Therefore, based on the information provided above, the following scatter plot and regression plot are obtained:
More Statistics calculators
You may also be interested in computing an exponential regression , or working out the subtleties of a polynomial regression , all of which apply in different contexts, based on the behavior of the observed sample data.
Likely, you will want to construct a scatter plot in order to assess the empirical behavior of the data, and to pre-assess if a logarithmic regression applies instead of a different type of regression.